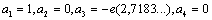Теперь, когда стали известны эвристический подход к исследовательским задачам и математический инструмент статистического моделирования, можем задаться вопросом: а нельзя ли облегчить труд исследователя при выработке конструкций исходных конструкций математических моделей?
Во взаимодействии «эвристик (эксперт) - математик», когда диалог происходит даже у одного и того же исследователя, вполне можно упростить процессы эвристического и эвроритмического моделирования, если заранее известно, что данный класс задач статистического моделирования соответствует устойчивым законам распределения. Нами здесь излагаются особенности применения биотехнического закона [1], претендующего на общность многих типов устойчивых распределений.
Вначале рассмотрим некоторые упрощающие допущения. Главным из них является изменчивость изучаемого объекта в исследуемом отрезке времени. Ученик А.А. Чупрова известный экономист-статистик О.Н. Андерсон (1887-1960) впервые «указал на особые сложности обеспечения однородности временных данных из-за появления новых факторов и структурных сдвигов» (Цит. по [2, с.163]).
В большинстве исследований в макромире позволено сделать аддитивную суперпозицию времени. Поэтому принимаем гипотезу, что введение различных шкал времени, когда за нуль одной шкалы принимается какой-то момент на хронологической шкале (например, по исчислению лет с новой эры, то есть с Рождества Христово), позволяет описывать неоднородности процессов во времени.
Допущения о возможности применения устойчивых законов распределения статистических данных, конечно же, не снимает полностью интуитивный аспект моделирования. На этапах количественной (параметрической) идентификации, описанных ранее в наших статьях, так же необходимы эвристические приемы. Однако предполагается, что стратегическая суть исследуемого процесса эвристически идентифицирована заранее по какой-то алгебраической формуле (то есть образуется процесс получения конечных результатов математических решений по Рене Декарту).
Для моделирования по распределениям статистик Р.А. Фишер (1925) предложил метод максимального правдоподобия. Он строго разграничивал параметры - неизвестные характеристики генеральной совокупности, и статистики - наблюдаемые характеристики. Фишер ввел понятия состоятельных, эффективных и достаточных характеристик, которые стали фундаментальными понятиями математической статистики [3, с.164].
Разный смысл в группировках факторов (статистик по Фишеру) требует более тщательного анализа эвристической модели биотехнического закона.
Переход от содержательности к ее математическому аналогу исключает семантику исходной задачи, лишает проблему её конкретности [4, с.43]. Вот здесь и кроется методологическая ловушка для неискушенных исследователей и математиков-программистов, которая может привести к точной параметрической, но ложной эвристической идентификации.
При решении задач управления, при принятии решений, как указывает Д.А. Поспелов [4], мы всегда сталкиваемся с двумя случаями. Либо перед нами задача, которую, в принципе, мы умеем решать и надо только найти решение данной конкретной задачи, либо мы сталкиваемся с совершенно неясной для себя проблемой, для которой даже неизвестно, с чего же даже начать для получения адекватных исходным данным моделей.
Поэтому здесь появляется, так называемая в филологии и психологии, пойнтер-точка [1]. Это очень характерная для исследователей ситуация, когда содержательные трудности и неопределенности в данных и знаниях (эвристиках) значительно сдерживают интерес к статистическому моделированию у многих ученых.
Здесь нами предполагается, что понятие «новая задача» имеет различные уровни определенности: она может быть известна специалистам, но оказаться новой только для конкретного исследователя (эта ситуация требует обучения); она может быть новой для специалистов нашей страны (эта ситуация требует проведения интенсивной пропагандистской работы); она может быть вообще новой для специалистов мирового научного сообщества, но в какой-то форме существовать в передовых отраслях науки и техники (необходима компиляция в данный класс задач); она принципиально новая в науке и технике (требуются так называемые фундаментальные исследования, прежде всего на эвристическом уровне и структурно-параметрическом изложении).
Понимание конкретной ситуации, в которой в данный момент времени находится исследователь, занимающийся статистическим моделированием собственных ил же чужих исходных данных, очень важно не только психологически (мера уверенности, чувство успешности решения задачи за заданный отрезок времени, понимание достаточности средств и ресурсов для решения задачи и пр.), но и методологически. Ведь чаще всего к статистическому моделированию приступают не из-за нехватки для поставленной задачи соответствующих математических методов, а прежде всего из-за боязни неадекватности затраченных сил и средств конечным результатам моделирования.
Понятия «модель» и «моделирование» попадают в первую сотню наиболее часто употребляемых слов общенаучной лексики [5, с.78]. Каждое из этих слов применяется как семантически очевидное. Однако словосочетание «быть моделью» имеет различные формы (морфизмы). По Ю.А. Гастеву [5] существуют различные логико-алгебраические аспекты моделирования, а также аналогия между понятиями «быть моделью» и гомоморфизмами.
Гомоморфизм - это отображение соответствия одного множества элементов (в нашем случае природной, природохозяйственной или эргатической системы) в другое (математическая модель), которое может быть однозначным и неоднозначным. Даже в физических моделях, например в изготовляемых машинах одной серии или партии, трудно обеспечить однозначность, так как хотя бы на некоторую малую погрешность отличаются друг от друга одинаковые по конструкции машины (по мощности, массе и другим параметрам). В биотехнических, а еще тем более в биологических, объектах неоднозначность повышается. Например, деревья одной породы столь не похожи по параметрам между собой, то есть они не изоморфны друг к другу.
В лесном деле по многим исследуемым объектам невозможны физические модели, например модель лесоучастка как некой части лесной экосистемы и др. В связи с этим возможности физического или физически-аналогового моделирования в инженерной экологии, защите природной среды и природообустройстве не столь велики, как это возможно в чисто технических системах. Поэтому во многих экологических, экономических и технологических (а тем более всё вместе) исследованиях математические модели оказываются единственно возможными объектами вычислительных экспериментов.
Биотехнический закон. Развитие разнообразия законов распределения показано в работе [6]. С середины 60-х годов нашего века, благодаря в основном трудам Б. Мандельброта, в экономике и других областях деятельности человека стали применяться «ближайшие родственники» нормального распределения (закона Гаусса). Устойчивые законы, не относящиеся к, по нашему мнению почему-то названному «нормальным», нормальному, имеют богатую перспективу применения. Они и есть в действительности «нормальные», а закон Гаусса-Лапласа является явно идеализированным, то есть по сути ненормальным.
Поэтому нами была выдвинута гипотеза о том, что любой устойчивый закон статистического распределения является деформированным, то есть асимметричным, циклом взаимодействия или нормального закона. Многие реальные явления в динамике описываются асимметричными циклами [7, 8, 9] или (в статике, как в «срезах» времени протекания какого-то процесса) числами Фибоначчи и золотым сечением [10].
Например, таблицы хода роста древостоев описываются асимметричными графиками нормального распределения. Однако это является искусственным притяжением нормального закона (идеального цикла) к описанию изменений реального явления (деформированного цикла). Поэтому необходимы особые законы распределения, как частный случай учитывающие и общеизвестный в классической математической статистике закон (нормального распределения) Гаусса-Лапласа.
Осмысление деформированности идеального цикла [11, 12] или, что то же самое применительно к статистике, асимметрия устойчивого нормального распределения Гаусса-Лапласа позволяет подойти к дедуктивному методу моделирования уравнением цикла или его части, которое было названо биотехническим законом. Причем эта формула биотехнического закона (или какая-то математическая конструкция из фрагментов биотехнического закона) сразу же (по Рене Декарту) приводит к конечным алгебраическим решениям. Такой подход пытался применить в робототехнике Э. Накано [13].
Для природохозяйствования сумма сил действия и противодействия, составляющая по абсолютной величине меру взаимодействия [14, c.9], переходит в общий принцип В.И. Вернадского. Он утверждал, что все экологические ниши на Земле остаются, в ходе регулярной смены биоценозов на другие, заполненными и суммарная масса биосферы достоверно не меняется.
По нашему мнению, эта общая масса биосферы в ходе его эволюции образует энергетический импульс жизни на планете. Еще раз подчеркнем, что направление сил [14] принимаем в виде стрелы времени по С. Хокингу. Поэтому биотехнический закон определяет изменение только величины сил взаимодействия. В наиболее общем виде биотехнический закон формулируется следующим образом: в процессах жизнедеятельности и эволюции биологических и биогенных объектов действие не равно противодействию. Равенство сил действия и противодействия (по третьему закону Ньютона) наблюдается только при переходе от роста к отмиранию, т.е. проявляется как частный (одномоментный во времени) случай [15, c.39]. В книге [15] и других публикациях на многих примерах (ныне более 50 000) показано существование биотехнического закона в различных количественных соотношениях взаимодействия как внутри, так и вне организмов. Можно обобщить, утверждая, что там, где есть взаимодействие, есть и проявление биотехнического закона [15, c.39].
Теперь, на основе последующих научных работ, мы утверждаем большее: там, где есть проявление биотехнического закона, там возможно (хотя бы фрагментарно) изучение реального цикла взаимодействия с учетом законов идеального цикла. Причем это изучение ныне перешло на так называемые вейвлет-сигналы в виде волновых уравнений.
Уравнение биотехнического закона. Для многих природных явлений характерно мультипликативное объединение (совместные события) действия и противодействия, поэтому биотехнический закон наиболее распространен в виде уравнения
![]() (1)
(1)
Анализ показал [15, c.42-46], что это уравнение наиболее удачно учитывает критические уровни развития объектов [16, с.7]: «Развитие подчиняется экспоненциальной или степенной зависимости и что имеется четкая регулярность в смене эволюционных этапов революционными перестройками. ...Чем значительнее революционные перестройки, тем реже они происходят и тем в более высокой степени фигурирует это число (то есть основание натуральных логарифмов)».
С позиций теории цикла [14] мы понимаем под революционными перестройками изменение направления сил взаимодействия, а под эволюционными этапами - неразрывное плавное изменение величины этих сил. Тогда становится очевидным, что формула (1) действительна только для эволюционных этапов, а обобщенное уравнение [15] может в конкретных видах отображать и революционные смены направлений. Если революционные малые сдвиги относительно нечувствительны, то формула (1) пригодна для характеристики общих тенденций (плавно изменяющихся эволюционных трендов).
Привычные для нас математические формулы чаще всего представляют собой конструкции из различных символов, связанных между собой алгебраическими или иными функциональными отношениями. Символы могут иметь функциональный произвольный смысл. Главной здесь считается конструктивная связь между элементами математических моделей. В то же время существуют законы физики, химии и других естественных наук, в которых символы математических структур имеют четкое
смысловое содержание. Таким же является конструкция формулы (1). Если нам привычны изображения материальной вещи в виде рисунка или чертежа, то идеальный объект, каким является математическая структура в виде формулы, не очень-то похожа на машину. По аналогии с предметно-функциональным анализом вещи, например топора [17], в табл. 1 приведено функционально-деятельностное описание элементов модели (1).
Таблица 1.
Описание структуры и функций формулы (1) биотехнического закона
|
Конструктивные элементы (носители функций) |
Технические функции конструктивных элементов |
|
E - формула (1)
V1 - значение x V2 - персональная ЭВМ V3 - исследователь V4 - другие инструменты и предметы (авторучка, бумага и т.д.)
|
F - однозначное или многозначное статистическое отображение значения x в значение y
идентификация E по искомым значениям a1... a4
|
|
E1 - математический конcтрукт
E2 - математический конструкт
E3 - оперативная константа |
F1 -закон аллометрического роста при
F2 - закон гибели при a3>0
F2´´´- закон торможения по Мальтусу при
F3 - объединение математических конструктов E1 и E2: X - совместные взаимозависимые события; + - несовместные независимые события Примечания: Знаки / и - можно представить как знаки X и + с изменением знаков a1...a4; в сложных конструкциях возможны любые оперативные константы |
|
E1.1 - элемент a1
E1.2 - элемент x
E1.3 - элемент a2
|
F1.1 - активность действия и влияния x на y при
F´ 1.1-начальное условие странного аттрактора (2) при итеративном влиянии F´´ 1.1 - уровень стабильности при a2=0
F1.2 - управляемая объясняющая переменная, как правило x>0 (для стоимостных и других показателей может быть долг x<0),причем F´ 1.2 - при значительном размахе значений во множестве возможно применение ln x,l q x и другое числовое масштабирование F1.3 - интенсивность действия, влияния x на y F´ 1.3- эластичность силы действия (ресурса при форме моделей типа Кобба-Дугласа) в производственных функциях |
|
E2.1 - exp
E2.2 - элемент a3
E2.3 - элемент x
E2.4 - элемент a4 |
F2.1 - основание натурального логарифма Примечание: возможны и иные оперативные константы-символы изменения силы противодействия (аналогично и силы действия) F2.2 - активность силы противодействия, влияния x на y F 2.3 = F 1.2 F´ 2.3 = F ´ 1.2
F2.4 - интенсивность противодействия, влияния x на y |
Примечания:1) параметры a1 ... a4 могут зависеть от x , то есть ![]()
![]()
![]()
![]() 2) элемент x может быть производной от других переменных, то есть
2) элемент x может быть производной от других переменных, то есть ![]() 3) показатель y может быть обобщенным критерием типа
3) показатель y может быть обобщенным критерием типа ![]()
Из данных табл. 1 видно, что структурно-функциональный анализ формул устойчивых законов возможен по аналогии с анализом функций материальных объектов. Отличие заключается только в том, что элементами табл. 1 являются абстрактные символы. Но они имеют четкие функциональные предназначения, которые «понимает» ПЭВМ.
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико-математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100с.
- Моисеев, Н.Н. Математические задачи системного анализа / Н.Н. Моисеев. - М.: Наука, 1981. - 488 с.
- Плошко, Б.Г. История статистики: Учебное пособие / Б.Г. Плошко, И.И. Елисеева. - М.: Финансы и статистика, 1990. - 295 с.
- Поспелов, Д.А. Моделирование рассуждений. Опыт анализа мыслительных актов /
Д.А. Поспелов. - М.: Радио и связь, 1989. - 184 с. - Екатеринославский, Ю.Ю. Управленческие ситуации: анализ и решения / Ю.Ю. Екатеринославский. - М.: Экономика, 1988. - 191 с.
- Золотарев, В.М. Устойчивые законы и их применения / В.М. Золотарев. - М.: Знание, 1984. - 64 с.
- Мазуркин, П.М. Реальные явления идеального цикла / П.М. Мазуркин // Циклы природы и общества. - Ставрополь: ЮРКИТ, 1996. -
С.72-87. - Мазуркин, П.М. Циклическое строение и развитие биологических и технических ценозов. // Циклы природы и общества / П.М. Мазуркин, А.А. Колесникова // Материалы III-й международн. Конференции. Вып. 1 и 2. - Ставрополь; Изд-во Ставроп. унив-та, 1995. - С.191-194.
- Сабанцев Ю.Н., Мазуркин П.М. Явления цикла в кризисе экономики / Ю.Н. Сабанцев, П.М. Мазуркин // Циклы природы и общества. - Ставрополь: ЮРКИТ, 1996. С. 187-190.
- Колесникова, А.А. Золотое сечение в акустике древесины / А.А. Колесникова,
П.М. Мазуркин, Т.А. Макарьева // Циклы природы и общества. - Ставрополь: ЮРКИТ, 1996. -С.98-98. - Мазуркин, П.М. Реальные явления идеального цикла / П.М. Мазуркин // Циклы природы и общества. - Ставрополь: ЮРКИТ, 1996. -
С.72-87. - Мазуркин, П.М. Золотое сечение в квантовых циклах взаимодействий / П.М. Мазуркии // Материалы VI Междунар. конф. «Циклы природы и общества». Ч.2. - Ставрополь: Изд-во Ставр. ун-та, 1998. -С.309-311.
- Накано, Э. Введение в робототехнику: Пер. с япон. / Э.Накано. - М.: Мир, 1988. - 334 с.
- Соколов, Ю.Н. Цикл как основа мироздания / Ю.Н. Соколов. - Ставрополь: ЮРКИТ, 1995. - 123 с.
- Мазуркин, П.М. Биотехническое проектирование (справочно-методическое пособие) / П.М. Мазуркин. - Йошкар-Ола: МарПИ, 1994. - 348 с.
- Жирмунский, А.В. Критические уровни в развитии природных систем / А.В. Жирмунский, В.Н. Кузьмин. - Л.: Наука, 1990. - 223 с.
- Мазуркин, П.М. Анализ технических функций / П.М. Мазуркин. - Марийск. политехн. институт. - Йошкар-Ола; 1989. - 111 с. - Деп. ВНИПИЭИлеспром, №2436-лб89.
Библиографическая ссылка
Мазуркин П.М. БИОТЕХНИЧЕСКИЙ ПРИНЦИП И УСТОЙЧИВЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ // Успехи современного естествознания. 2009. № 9. С. 93-97;URL: https://natural-sciences.ru/ru/article/view?id=12854 (дата обращения: 08.03.2026).




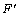 -при числовых множествах {x} и {y}
-при числовых множествах {x} и {y}
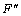 - при заданных и a1 ...a4 восстановление некоторых значений множества {x} интерполированием
- при заданных и a1 ...a4 восстановление некоторых значений множества {x} интерполированием
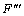 - при заданных и a1 ...a4 аппроксимация {x´} > {x} некоторых значений экстраполяцией
- при заданных и a1 ...a4 аппроксимация {x´} > {x} некоторых значений экстраполяцией
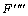 - при заданных {x}, {y} , и a1 ...a4 фильтрация новых значений
- при заданных {x}, {y} , и a1 ...a4 фильтрация новых значений 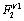 - критерий Жирмунского-Кузьмина при
- критерий Жирмунского-Кузьмина при