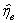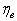Метод - это способ достижения определенного результата в познании или на практике [3, с.149]. Способ определяет некоторый порядок выполнения действий, в нашем случае с исходной статистической выборкой. Поэтому показаны свойства биотехнического закона как инструмента, используемого при работе над «изготовлением» математической модели.
По аналогии с созданием технического объекта исследователю необходимо «изготовить» математическую модель для конкретных условий функционирования, то есть создать и идентифицировать экспериментальный образец исходной модели функционирования природной или эргатической (природно-антропогенной или только антропогенной) системы. По ходу изготовления конструкция модели может видоизменяться (как правило, конструкция модели будет упрощаться) в сходимости по выходным результатам к объекту исследования [1].
После доводки экспериментального образца модели встает задача серийного ее использования, то есть новая параметрическая идентификация: а) к другим условиям функционирования данной системы по данным следующих статистических выборок; б) к другим объектам, однородным к изученному объекту по структуре, действиям и условиям функционирования.
На рис. 1 приведена схема процесса решения задач с использованием ПЭВМ.
По этой схеме некоторый реальный процесс (явление - это есть мгновенный срез процесса) должен быть описан по определенной методике мысленного эксперимента путем последовательного (циклического) изучения и уяснения задачи (в нашем случае задачи получения добротной математической модели). В процессе изучения происходит отображение реального исследуемого процесса на определенные понятия и опыт исследователя [1].
Этот этап является психологически трудным, так как прежде всего здесь значительна опасность ложной эвристической идентификации фактов и факторов (переложение свойств объекта в категории факторов) и их взаимодействий. Поэтому необходима многократная повторность (если один исследователь) или применение экспертных методов для многовариантного мысленного отображения исследуемого объекта.
Путем абстрагирования (на следующем этапе), то есть исключения материальной ткани от её сущностного функционально-деятельностного каркаса, создается словесное описание исследуемого объекта. Такое сочинение на заданную тему образует эвристическую модель. Она, как правило, содержит мало количественных данных, но много известных и предполагаемых априори знаний. Однако это сочинение содержит также много двусмысленностей, что характерно для естественного языка, и неясностей (зависит от стиля писателя), а иногда и непонятных выражений (отличия в терминах) и т.п.
Для повышения определенности описания и однозначности терминов необходимо составить эвроритм, т.е. алгоритм в интуитивном смысле. В этой модели элементами являются четкие по конструкции словосочетания.
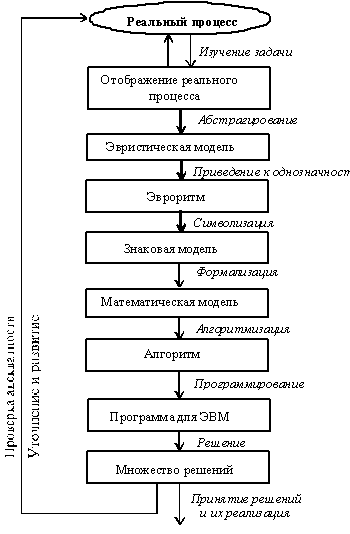
Рис. 1. Схема (эвроритм) решения инженерных (творческих, требующих знаний, умений и навыков изобретательства) задач с применением ПЭВМ
Такие эвроритмические описания могут быть смоделированы методами моделирования рассуждений [4, 5], которые позволяют повысить адекватность содержательного описания объекта моделирования. Главное здесь не количественные характеристики, а связи между фактами и элементами знаний (фреймами) об объекте исследования.
Наиболее наглядно эвроритмы можно представить в виде блок-схем, методика построения которых изложена в стандартах ЕСПД. От алгоритма для ПЭВМ эвроритм отличается тем, что в блоках приводятся не формулы, а словесные предложения [7], например, в виде технических функций [6]. На этой основе затем были созданы два метода [8] - поискового проектирования технологических комплексов и поискового конструирования их взаимно увязанных о биотехническим функциям технических компонентов.
Остальные этапы по схеме на рис. 1 хорошо известны. При построении знаковых моделей применяются общепринятые символы и условные обозначения. Качественное (эвристическая модель, эвроритм) и количественное (числовые значения факторов) в процессе моделирования могут соотноситься по-разному. Это зависит от подготовленности информации, от опыта исследователя и многих других особенностей.
Рассмотрим только наиболее характерные отношения по предельным значениям условной оси «определенность-неопределенность». Очевидно, что полная неопределенность в качественной и количественной исходной информации приводит к дилетантству, к поверхностным или общим рассуждениям. Особенно этот случай важен тогда, когда одну и ту же задачу вместе решают специалист и математик-программист. В этом случае между ними не получится технологического взаимодействия. Поэтому лучше всего, если в одном исследователе имеются свойства и специалиста и программиста-пользователя ПЭВМ.
Тогда можно рассмотреть три варианта сочетания предельных значений информированности: 1) количественные данные известны, а качественные знания о задаче неизвестны (неопределенными были еще в прошлом, утеряны со временем или не публиковались); это задачи на восстановление сущности по количественным данным; 2) количественные данные неизвестны, но содержательная часть в виде гипотезы определена; это класс задач, чаще всего расставляемых исполнителям руководителями в сферах управления, науки, техники, экономической теории и др., то есть задачи на восстановление количественных данных (по экспериментам, систематизации статистических данных и т.д.); 3) количественная и качественная информация по задаче определена; это - задачи на моделирование или перемоделирование (если конструкции ранее приняты аппроксимацией, например, в виде полиномов).
В первом случае применяют существующие знания для объяснения таблиц данных. При моделировании могут быть использованы известные математические конструкты. Хотя из самой матрицы данных можно «выловить» какое-то содержание, но в основном здесь применяют методы аппроксимации линеаризуемыми математическими функциями. Если по минимуму содержательности, получаемой из анализа самой таблицы, можно сделать заключение о соответствии данных устойчивому закону распределения (выполняют дисперсионный и корреляционный анализы, проверку на устойчивые законы распределения), то в этом случае возможно применение методов идентификации. В реальных задачах полной неопределенности в содержательности не бывает, поэтому здесь моделирование вполне возможно.
Во втором случае речь идет о логичности и доказательности только самой рабочей гипотезы. Во многих областях науки накоплены типовые содержательные ситуации, по которым можно судить о характере будущих количественных данных. Ни один эксперимент не проводится без эвристического предположения об ориентировочных оптимумах, границах изменчивости факторов и других условиях. В этом случае восстановление количественных данных - как говорят - «дело техники». Многие объекты исследования несомненно подчиняются устойчивым законам (недобросовестность в описании содержания и получении исходных данных мы исключаем) развития, строения и взаимодействия. Поэтому эвристическое понимание существенно облегчается и практически накоплен такой богатый материал, что необходима состыковка данных с обновляющимися знаниями в информационных технологиях.
В чистом виде случай содержательного моделирования, без приведения числовых данных, очень распространен. Во многих случаях достаточно просто понять характер явления или процесса, а для принятия управленческих решений иногда количественных данных даже и не требуется. Однако массовость этого случая превышает все разумные меры, из-за этого происходят социально-экономические кризисы, поэтому необходимо какое-то рациональное соответствие между всеми тремя случаями моделирования.
В третьем случае структурная определенность математической модели наиболее высока и она недостаточно достоверна для формирования новых знаний и теорий. Вот этот процесс качественно-количественного анализа и синтеза называется эвристико-статистическим моделированием. Здесь структурная определенность находится на первом месте, а количественная интерпретация рабочей гипотезы - на втором. Тогда критериями адекватности становятся: 1) понимание сущности объекта моделирования; 2) добротность, полнота и оперативность получения исходных количественных данных.
Примеры проявления биотехнического закона. Биотехнический закон проявляется как фрагмент циклично-волнового процесса даже в абиотических веществах, например, в поведении металлов. Например, в книге [9, с.177, рис.107] приведен график зависимости предела прочности 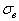 при растяжении стали 40 в зависимости от температуры. Для интервала температуры
при растяжении стали 40 в зависимости от температуры. Для интервала температуры 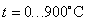 была получена математическая модель предела прочности (Мпа)
была получена математическая модель предела прочности (Мпа)
![]() (1)
(1)
при максимальной относительной погрешности 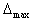 =30,0% .Таким образом, из-за стрессового возбуждения структуры стали на изменение температуры нагрева предел прочности у стали 40 при 300 оС даже выше, чем при нулевой температуре.
=30,0% .Таким образом, из-за стрессового возбуждения структуры стали на изменение температуры нагрева предел прочности у стали 40 при 300 оС даже выше, чем при нулевой температуре.
Биотехнический закон хорошо проявляется в процессах преобразования химической энергии в механическую, например в двигателях внутреннего сгорания.
Характеристики двигателей. При проектировании машин и агрегатов с двигателями внутреннего сгорания (ДВС) применяют несколько методологических подходов. Во-первых, это применение методов определения и прогнозирования динамических нагрузок, необходимых для обоснованных расчетов на прочность и долговечность [10]. Во-вторых, это использование методов расчета энергосиловых показателей, характеризующих интенсивность взаимодействия инструментов, рабочих органов и машин с предметом обработки.
Очевидно, что в обоих случаях необходимо учитывать динамику изменения различных характеристик ДВС. Потребность в простых математических моделях скоростных, нагрузочных и иных характеристик возникает также при обосновании технологических процессов, в которых применяется то или иное устройство. Модели характеристик ДВС, прежде всего, необходимы при обосновании режимов механической обработки почвы, грунта и других материалов. Для лесных деревообрабатывающих машин [11] известны следующие подходы:
а) моделирование физико-механических свойств древесины растущих деревьев и их учет в энергосиловых расчетах, например, спиливания цепными пилами [12]; б) аналитическое и экспериментальное изучение элементарного резания, а затем с помощью нескольких видов расчетных методик переход к обоснованию параметров реальных видов инструментов и режимов резания в различных условиях [13]; в) аналитическое и экспериментальное изучение множества вариантов конструкций у механизмов резания; г) по предыдущим пунктам решение обратных задач по заданной мощности двигателя, а также, в соответствии с математическими моделями [12, c.88 - 97], определение допустимой мощности привода по условиям работоспособности механизмов резания и их деталей.
В последнем случае необходимо знание не только номинальной мощности ДВС, но и изменения значений мощности в зависимости от частоты вращения коленчатого вала. В качестве примера смоделированы характеристики ДВС бензомоторной пилы типа МП-5 "Урал" [14] и дизеля Д-442-22 Алтайского моторного завода.
Скоростная характеристика ДВС бензопилы включает в себя несколько зависимостей. При изменении частоты вращения от 4,55 до 6,55 тыс. об/мин по данным [14,c.83] получены следующие математические модели регрессии:
- мощность двигателя N e ,л.с.
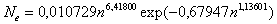 ; (2)
; (2)
- удельный расход топлива g e , г/л.с.ч
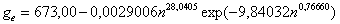 . (3)
. (3)
Экспериментальные и расчетные значения (во всех моделях сохранена размерность показателей, приведенная в первоисточнике [14]) по моделям (2) и (3) приведены в табл. 1.
Таблица 1. Изменение мощности и удельного расхода топлива двигателя бензиномоторной пилы
|
n |
N^ e |
N e |
|
|
n |
g^ e |
g e |
|
|
|
4.60 5.00 5.40 5.80 6.20 6.40 6.55 |
4.10 4.80 5.33 5.70 5.90 5.95 5.93 |
4.11 4.79 5.33 5.71 5.91 5.94 5.93 |
-0.01 0.01 -0.00 -0.01 -0.01 0.01 -0.00 |
-0.19 0.28 -0.01 -0.13 -0.09 0.21 -0.07 |
4.55 4.80 5.00 5.40 5.80 6.20 6.55 |
500 450 420 405 415 437 470 |
491 454 430 403 407 437 474 |
9.18 -4.02 -10.15 1.53 7.57 0.42 -4.27 |
1.84 -0.89 -2.38 0.38 1.82 0.10 -0.91 |
Из табл. 1 видно, что относительная максимальная погрешность 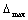 < 2,5% для моделей N e и g e , т.е. уравнения (2) и (3) для описания характеристик ДВС бензопилы можно использовать с доверительной вероятностью не ниже 97,5%.
< 2,5% для моделей N e и g e , т.е. уравнения (2) и (3) для описания характеристик ДВС бензопилы можно использовать с доверительной вероятностью не ниже 97,5%.
Дизель Д-442-22 (№4380, т.н. №579945) по экспериментальным данным Алтайского моторного завода для начального удельного расхода топлива g e0 = 163,7 г/л.с.ч имеет следующую скоростную характеристику (табл. 2)
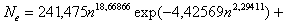
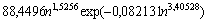 (4)
(4)
при n = 1,2 ...1,8 тыс. об/мин.
Таблица 2. Изменение мощности двигателя Д-442-22
|
n, тыс. об/мин |
N ^ e, л.с. |
N e, л.с. |
|
|
|
1200 1300 1400 1500 1600 1700 1725 1751 1763 1777 1800 |
109.0 118.0 123.0 125.0 124.0 121.0 121.0 121.0 121.0 121.0 117.0 |
109.0 118.0 123.1 124.7 124.1 122.1 121.3 120.5 120.1 119.6 118.6 |
0.01 -0.01 -0.09 0.29 -0.10 -1.06 -0.34 0.50 0.90 1.44 -1.63 |
0.01 -0.01 -0.08 0.23 -0.08 -0.88 -0.28 0.41 0.75 1.19 -1.40 |
Из табл. 2 видно, что модель (4) с высокой точностью описывает изменение мощности дизеля. При этом фактические значения n достигают 1843 об/мин. Однако в диапазоне 1800...1843 об/мин модель (4) имеет более высокую погрешность. Общеизвестно, что эксплуатационная частота вращения дизеля n < 1,8 тыс.об/мин.
Формула (4) содержит две, одинаковые по структуре, составляющие. Вторая составляющая характеризует приспособляемость двигателя к внешним нагрузкам. Коэффициент приспособляемости будет вычисляться по отношению ко второй части формулы (4). Формулы (2) и (4) обладают простотой в сравнении с известной для машиностроителей формулой Лейдермана
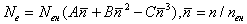 , (5)
, (5)
в которой необходимо знать дополнительно факторы: 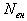 - номинальная мощность;
- номинальная мощность; ![]() - номинальные обороты ДВС; А, В, С - эмпирические коэффициенты для типа двигателя.
- номинальные обороты ДВС; А, В, С - эмпирические коэффициенты для типа двигателя.
Причем в формуле (2) при расчетах можно не знать значений номинального числа оборотов и номинальной мощности. Нагрузочной характеристикой называют зависимость расхода топлива и других показателей от мощности ДВС при заданном числе оборотов коленчатого вала. По данным [14, c.84] при n = 5800 об/мин в интервале N e = 0,75 ...5,75 л.с. нами были получены регрессионные модели (табл. 3):
- удельный расход топлива, г/л.с.ч
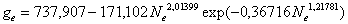 ; (6)
; (6)
- часовой расход топлива, кг/ч
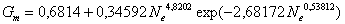 . (7)
. (7)
Таблица 3. Изменение удельного и часового расхода топлива при n = 5800 об/мин
|
N e л.с. |
Удельный расход топлива, г/л.с.ч |
Часовой расход топлива, кг/ч |
||||||
|
g^ e |
g e |
|
|
G^ m |
G m |
|
|
|
|
0.75 1.50 2.00 3.00 4.00 5.00 5.75 |
720 500 400 370 380 420 450 |
664 526 444 352 355 415 474 |
56.1 -25.8 -43.7 18.0 25.0 4.9 -24.2 |
7.8 -5.2 -10.9 4.9 6.6 1.2 -5.4 |
0.71 0.75 0.87 1.25 1.64 2.05 2.33 |
0.69 0.77 0.88 1.23 1.65 2.06 2.32 |
0.020 -0.018 -0.010 0.025 -0.008 -0.009 0.006 |
2.8 -2.4 -1.2 2.0 -0.5 -0.4 0.3 |
Из табл. 3 видно, что модель (6) адекватна экспериментальным данным с доверительной вероятностью около 90%, а модель (7) - более 95%. Предложенные зависимости позволяют создавать различные типы имитационных моделей.
Эргатическая система. Операторы лесозаготовительных машин достигают полной производительности после некоторого периода обучения и практической работы для адаптации к новой машине. По данным ФМГ «Тимберджек» доля выработки от нормального уровня производительности изменяется в соответствии с уравнениями (табл. 4):
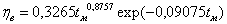 - комплекс (ВПМ + трелевщик) ; (7)
- комплекс (ВПМ + трелевщик) ; (7)
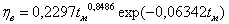 - комплекс (харвестер + форфордер) , (8)
- комплекс (харвестер + форфордер) , (8)
где t M - время практической работы оператора на новой машине (0 .. 9 месяцев для первого комплекса машин и 0 .. 17 месяцев для второго, по технолоии более сложного).
Таблица 4. Доля производительности оператора машины от опыта
|
Время обучения t M,мес. |
Валочно-пакетирующая машина |
Харвестерная машина для сортиментов |
||||||
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 6 7 9 12 |
0.29 0.50 0.66 0.77 0.85 - 0.93 1.00 - |
0.30 0.50 0.65 0.76 0.85 - 0.95 0.99 - |
-0.01 0.00 0.01 0.01 0.00 - -0.02 0.01 - |
-3.5 0.0 1.5 1.3 0.0 - -2.2 1.0 - |
0.20 0.36 0.49 0.60 0.66 0.71 - 0.81 0.90 |
0.216 0.364 0.482 0.578 0.656 0.718 - 0.830 0.884 |
-0.016 -0.004 0.008 0.022 0.004 -0.008 - -0.020 0.016 |
-8.0 -1.1 1.6 3.7 0.6 -1.1 - -2.5 1.8 |
Таким образом, технологическое взаимодействие должно рассматривать процессы теоретического обучения, приобретения практических навыков и опыта по повышению производительности труда совместно как единый технологический процесс динамического совершенствования как персонала, так и технологического (в нашем случае лесозаготовительного) комплекса.
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико-математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100с.
- Ломов, Б.Ф. Принцип активного оператора в инженерной психологии / Б.Ф. Ломов // Наука и человечество. Международный ежегодник. - М.: Знание, 1982. - С.53-67
- Попов, Е.В. Гносеологическая сущность технического творчества / Е.В. - Воронеж: Изд-во Воронежского университета, 1977. - 172 с.
- Поспелов, Д.А. Моделирование рассуждений. Опыт анализа мыслительных актов /
Д.А. Поспелов. - М.: Радио и связь, 1989. - 184 с. - Поспелов, Г.С. Искусственный интеллект - основа новой информационной технологии / Г.С. Поспелов. - М.: Наука, 1988. - 280 с.
- Мазуркин, П.М. Анализ технических функций / П.М. Мазуркин. Марийск. политехн. институт. - Йошкар-Ола; 1989. - 111 с. - Деп. ВНИПИЭИлеспром, №2436-лб89.
- Мазуркин, П.М. Оформление дипломных и курсовых проектов / П.М. Мазуркин // Методические указания для студентов технологических специальностей. - Йошкар-Ола: МарПИ, 1977. - 32 с.
- Мазуркин, П.М. Методы поискового проектирования / П.М. Мазуркин, А.И. Половинкин; Марийск. политех. ин-т. - М., 1989. - 103 с. - Деп. в НИИВШ, №908-89.
- Некрасов, С.С. Сопротивление хрупких материалов резанию / С.С. Некрасов. - М.: Машиностроение, 1971. -186 с.
- Александров, В.А. Моделирование технологических процессов лесных машин: Учебник для вузов Ъ В.А. Александров. - М.: Экология, 1995. - 256 с.
- Мазуркин, П.М. Функциональная классификация лесных машин / П.М. Мазуркин // Лесной журнал. - 1994. - №1. - С.47-50.
- Люманов, Р. Машинная валка леса /
Р. Люманов. - М.: Лесн. пром-сть, 1990. - 280 с. - Любченко, В.И. Резание древесины и древесных материалов: Учеб. пос. / В.И. Любченко - М.: Лесн. пром-сть, 1986. - 296 с.
- Моторные инструменты для лесозаготовок (теория, конструкция, эксплуатация) / Полищук А.П., Шмаков Д.К., Кретов В.С. и др. - М.:Лесн. пром-сть, 1970. - 232 с.
Библиографическая ссылка
Мазуркин П.М. БИОТЕХНИЧЕСКИЙ ЗАКОН И СОДЕРЖАТЕЛЬНАЯ АДЕКВАТНОСТЬ МОДЕЛИ // Успехи современного естествознания. 2009. № 9. С. 115-121;URL: https://natural-sciences.ru/ru/article/view?id=12862 (дата обращения: 04.03.2026).




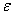
 , %
, %