Заметим здесь, что «наибольшее соответствие» может быть чисто количественное (аппроксимация) или же с учетом еще и сущности исследуемого объекта (идентификация). Функцией ошибки сходимости у выходных результатов модели и объекта является сумма квадратов остатков (метод МНК). Однако в некоторых случаях [3] могут быть использованы и другие критерии качества модели: сумма остатков, максимальный остаток по модулю (в американской решающей среде «EUREKA» для ПЭВМ) и др.
Регрессионная модель основана на аналитическом представлении линии регрессии, то есть воображаемой траектории вглубь по времени у собранных в прошлом данных. Эта линия является детерминистской частью взаимосвязи факторов и важнейшей характеристикой корреляционной связи с помощью математической функции, называемой регрессионным уравнением. По нашей методологии [1] сразу же отметим, что линия регрессии является малой частью волновых закономерностей с периодичностью, значительно превышающей период проведения измерений. Поэтому все явления и процессы есть волновые процессы.
Условно принято называть средние значения зависимой переменной (показателя) теоретическими значениями [4, с.309, с.311]. Каждая из моделей корреляционной связи приближенно, то есть некорректно, характеризует объективную связь явлений, определенную их качественной природой. Нужно также заметить, что среднее арифметическое значение от всей статистической выборки часто приводит к ложной идентификации. Это происходит из-за того, что одно и то же среднее может оказаться у большого множества статистических распределений по отдельным точкам.
Поэтому при прочих равных условиях регрессионная модель дает более надежные оценки. В регрессионной модели ее параметры оцениваются по данным о всей совокупности имеющихся статистических данных [4, с.314]. Таким образом, нельзя бездумно отбрасывать или прибавлять данные, как это ухищряются делать экономисты и социологи, но этому никак не приучены еще биологи и экологи, так как каждая особь в популяции значима .
На практике часто встречаются задачи с оценкой изменения одного выходного результата по множеству входных факторов (заметим здесь, что многофакторные задачи решаются по однофакторным статистическим моделям бинарных отношений). Наилучшая оценка адекватности у результатов модели и объекта исследования получается при использовании метода наименьших квадратов. Он дает меру оценки расстояний между теоретическими и фактическими результатами. В итоге получается, что для всей модели сумма квадратов отклонений (часто называют остатками от модели) определяет среднегеометрическое расстояние между теоретической и эмпирической линиями регрессии. Поэтому остатки в дальнейшем принимаются за новую статистическую выборку, относительно которой возможно применять все процедуры идентификации устойчивыми законами распределения, а также применять формулы адекватности и сходимости модели к фактическим данным.
Для обобщенного описания возможных форм математических моделей примем следующие обозначения: x - объясняющие переменные; y - показатели, т.е. оценочные переменные. Множество представим в виде двух подмножеств: x 0- объясняющие переменные, влияние которых, после идентификации биотехнического закона и его фрагментов в виде известных устойчивых законов распределения, становится малозначимым на выбранный критерий оптимальности; x - переменные, влияние которых значимо.
Отсюда следует, что x: = x 0 + x , и обобщенное уравнение математической модели, например, можно записать в виде
![]() ,(1)
,(1)
где a 0, a - параметры активности влияния переменных,
- x 0 - «нулевые» факторы, т.е. такие, которые имеют почти нулевую значимость влияния на изучаемые исследователем показатели,
- y - показатели, в общем случае такие же, как и x , многомерные переменные факторы,
- x - значимые объясняющие переменные,
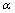 - параметры интенсивности влияния объясняющих переменных,
- параметры интенсивности влияния объясняющих переменных,- U - объединение частных функций в виде фрагментов биотехнического закона или его целиком с использованием оперативных констант.
Для «нулевых» объясняющих переменных a = 0 , поэтому наблюдается нулевая их интенсивность. Значения a 0 объединяются в одну постоянную, которая будет отражать инертность влияния всех неучтенных факторов, то есть принцип «не влияния».
Значения фактических выходных результатов объекта y^ будут
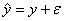 , (2)
, (2)
где ![]() - остатки, по которым оценивается сходимость выходных результатов объекта исследования и конструируемой математической модели.
- остатки, по которым оценивается сходимость выходных результатов объекта исследования и конструируемой математической модели.
Объединение U возможно на основе применения различных сочетаний оперативных констант (+, -, х, /, sin, cos , exp и т.п.). Многомерные переменные 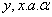 могут образовать весьма сложные конструкции с использованием в одной модели биотехнического закона, но при использовании их фрагментов и различного вида оперативных констант.
могут образовать весьма сложные конструкции с использованием в одной модели биотехнического закона, но при использовании их фрагментов и различного вида оперативных констант.
Интенсивность действия переменных может быть представлена в виде частных функций
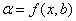 , (3)
, (3)
а сама объясняющая переменная с учетом явлений автоматического обратного влияния (авторегрессии) может иметь вид
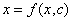 , (4)
, (4)
Если выходные результаты влияют на сами объясняющие переменные, что характерно для развивающихся систем с расширенным воспроизводством ресурсов (например, часть прибыли направляется на развитие и расширение производства), то получим модель в неявном виде, в которой
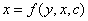 . (5)
. (5)
Во время идентификации или аппроксимации поле информации сжимается вдоль оси времени, хотя регистрация значений переменных у модели происходит в реальном режиме. Во время эксплуатации созданной модели, то есть готовой статистической модели, позволяющей в последующим отбросить табличную модель и применять математическую, необходимо учитывать фактор времени и соответствующим образом ее реконструировать.
Обозначим все параметры модели одним множеством
![]() .(6)
.(6)
Тогда с учетом развертки во времени получим
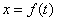 ,(7)
,(7)
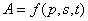 , (8)
, (8)
где t - время текущее, 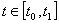 , - параметры евклидова пространства, s - целостные свойства изменения условий природной, природно-антропогенной, антропогенной или же эргатической системы. Множества p, s, t в совокупности образуют гиперпространства изменения переменных. Свертки этих множеств происходят следующим образом:
, - параметры евклидова пространства, s - целостные свойства изменения условий природной, природно-антропогенной, антропогенной или же эргатической системы. Множества p, s, t в совокупности образуют гиперпространства изменения переменных. Свертки этих множеств происходят следующим образом:
- для времени
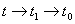 ;
; - для евклидова пространства: p = 0 - объект с сосредоточенными параметрами;
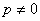 - объект с распределенными параметрами;
- объект с распределенными параметрами; - для целостных (системных) свойств s = 0 - условия постоянны.
Например, при условии s = 0 пусть постоянно увеличивается температура и (или) давление в среде функционирования технической системы. Тогда эти изменения влияют на соответствующее поведение системы. Другой пример. Пусть эргатическая система «входит» в среду с повышающейся температурой (пожарник с оборудованием в горящее здание). Очевидно, что выходные результаты через изменение параметров А будут различными при различном уровне температуры. В производственно-технических системах удается упростить математическую модель, если ее разрабатывать только для конкретного отрезка времени, локального пространства и конкретно заданных условий функционирования. Соответственно значения 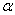 также превращаются в параметры. В этом случае возможны случаи:
также превращаются в параметры. В этом случае возможны случаи:
1) оперативные константы арифметические (+, -), то получим при 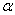 =1 класс линейных уравнений; 2) по п. 1 при
=1 класс линейных уравнений; 2) по п. 1 при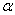 =1,2,3... получим полиномы;
=1,2,3... получим полиномы;
3) оперативные константы алгебраические (х, / ), то получим класс производственных функций с произведениями частных функций.
Далее рассмотрим некоторые частные случаи математической модели по формуле (1).
1. Интуитивный принцип объемности описывается соотношением [4, с.13]
y = x (9)
Здесь все параметры модели свернулись к единице. Такая модель связи многомерных переменных имеет реальную основу, например, в сфере потребления, складском хозяйстве, в идеальной таблице типа «затраты-выпуск» В. Леонтьева, квадраты Саати и т.п.
2. С учетом значимости в абсолютных значениях (весовых коэффициентов) получим
y = ax (10)
Такие линейные одномерные и многомерные модели хорошо известны, например, для решения балансовых и транспортных задач и др.
3. С учетом коэффициентов инертности и значимости переменных x 0 и x получим
y = a 0 + ax. (11)
Такие линейные модели наиболее распространены в математической экономике, причем при описании аддитивных процессов с независимыми друг от друга факторами. Но все ученые слишком увлеклись линейными отображениями. В действительности они могут быть применены только на короткие отрезки времени и очень короткие промежутки изменения других типов переменных. Кусочно-линейная аппроксимация всегда опасна тем, что неизвестны точки начала и конца каждого куска прямого отрезка.
4. Для описания выходных результатов производственно-технических систем используются модели, где объяснение происходит по знакам умножения (деления)
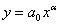 . (12)
. (12)
Такие модели эффективно используются в машиностроительных производствах (форма Кобба-Дугласа, Леонтьева и др.). они действительно там, где нет предыстории изучаемого процесса и взаимного влияния учтенных в исследовании факторов.
Обобщенная форма записи (1) в основном имеет, кончено же, только методологический смысл и она сама по себе не пригодна для машинных процедур идентификации. Возможность создания универсальной экономико-математической модели сомнительна и практически это нецелесообразно. В каждом конкретном случае необходимо проводить «свой» системный анализ, подчиненный определенным исследовательским целям.
Но, по принципу «от простого к сложному» можно предложить (табл. 1) «кирпичики» для построения по ходу структурно-параметрической идентификации биотехнического закона.
Таблица 1. Математические конструкты для построения статистической модели
|
Фрагменты без предыстории изучаемого явления или процесса |
Фрагменты с предысторией изучаемого явления или процесса |
|
y = ax - закон линейного роста или спада (при отрицательном знаке перед правой стороной приведенной формулы) |
y = a - закон не влияния принятой переменной на показатель, который имеет предысторию значений |
|
y = ax b - закон показательного роста (закон показательной гибели y = ax -b не является устойчивым, из-за бесконечности при нулевом значении объясняющей переменной |
|
|
|
|
|
|
|
В табл. 1 все «нормальные» фрагменты, у которых впереди могут быть оперативные константы в виде знаков «+» или «-». При этом при моделировании временных рядов тренд нужно вначале искать по закону экспоненциального роста или гибели (спада). Все шесть устойчивых законов распределения являются частными случаями биотехнического закона.
Статистические показатели идентификации. Критерии идентификации - это совокупность критериев оптимальности и верификации. Пусть значения переменных модели получены на основе количественных измерений (не количественные переменные ранжируются и (или) получают квалиметрические оценки). Критерии могут быть эвристическими и формальными. Эвристические критерии самоорганизации нами рассматривались в предыдущих статьях.
Если y - множество показателей, то есть факторов, принятых за характеристики изучаемого явления или процесса, то критерий оптимальности должен «увязать» вместе эти показатели, т.е. происходит многокритериальная свертка [5], что в общем виде можно записать
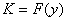 , (13)
, (13)
где K - принятый критерий оптимальности, F - целевая функция, y - показатели.
При неявно заданных функциях показателей получим
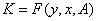 . (14)
. (14)
При многомерности критериев их можно свернуть, например, по обобщенному критерию технической полезности, биотехнической полезности и др. Причем множество критериев может иметь сложную взаимосвязь.
В реальных условиях производственные процессы сильно динамичны, особенно в добывающих отраслях. Например, моделирование процессов добычи угля в шахтах встречает серьезные трудности [6, с.32] при получении частных функций и соответственно частных критериев.
Критериальные модели (13) и (14) являются весьма сложными, особенно с учетом многокритериальности. Чрезмерное увеличение сложности модели, в попытках охватить все желаемое, не приводит к успехам. Как отмечается в [6. с.22], увеличение времени расчетов на ЭВМ обходится очень дорого, причем в большинстве случаев из-за недостаточной оперативности принимаемых после долгих расчетов решений. Кроме того, иерархически усложненные модели становятся неоперативными в режиме реального времени, так как время расчетов по прогнозированию становится больше, чем период упреждения прогноза на АСУТП и АСУП. Поэтому на практике очень эффективны модели явного типа
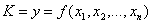 . (15)
. (15)
Проблема критериев в моделировании занимает центральное место. Одни утверждают, что необходим единый критерий в экономических оценках эргатических систем, другие - такой критерий создать невозможно. Но методология идентификации биотехнического закона обходит эту проблему, не создавая вообще моделей по обобщенным критериям.
Однако теоретически имеет смысл представить, что в гиперпространстве p,s,t мы можем описать динамику функционирования эргатической системы, а в пространстве p,t - изменение совокупности показателей. В эвклидовом пространстве можно описать статику системы, то есть физическую структуру.
Если все физические величины в конечном итоге выводятся из трех мер (метр, килограмм, секунда), то можно ли с их помощью оценить хозяйственную деятельность? Анализ показывает, что таким критерием является производительность (труда, процесса) или продуктивность (растений и животных), которую можно выразить через три главные физические величины.
Обобщенная оценка функционирования эргатической системы требует учета и будущего труда, особенно с учетом экологических последствий от хозяйственной деятельности. По мнению проф. П.Г. Олдака [7, с.49] все существующие показатели своим содержанием имеют определенную меру представленного продукта прошлого и живого труда. Отрицательное воздействие на природу позволяет выделить категорию затрат будущего труда (после затрат). Необходимо при этом учитывать границы допустимых нагрузок на природные комплексы, то есть пределы роста любой деятельности по результатам.
Отсюда следует, что в основе выбора максимально обобщенного критерия оптимальности функционирования эргатической системы лежат два основополагающих принципа: 1) критерий - это сам человек с его потребностями (для лесотехнической системы еще и учет потребностей леса); 2) критерий - это будущее жизни человека (леса и человека).
Этим принципам удовлетворяет совпадение только по номенклатуре (качеству) и значениям (количеству) целевых, плановых и директивных показателей, а также совпадение с их значениями собственных оценок фактических текущих результатов производственно-технологической системы. Это и будет общим критерием природохозяйственной деятельности, который требует создания программно-целевых экономико-математических моделей технических и технологических взаимодействий.
Здесь наблюдается важное методологическое следствие: если физика и химия нашли меру в прошлом (метр и килограмм относительно Земли), то мера экономики и экологии находится в будущем (в целевой модели сверхдальнего развития). А время для обоих указанных мер является однозначно связующим звеном, то есть между физикой и химией, с одной стороны, с экологией и эконометрикой - с другой.
В частных исследованиях взаимодействие человека и машины можно предсказать в виде критериев производительности работы (для машины) или труда (для человека). При этом качественное своеобразие и неповторимость статистических совокупностей обязывают интерпретировать их только применительно к конкретным условиям места и времени функционирования (поведения). Чтобы перенести эти оценки на другие статистические совокупности, необходимо доказать на основе качественного анализа идентичность комплекса условий и свойств окружающей среды.
Показатели имеют сильную косвенную значимость. Например, в работе [8, с.80] отмечается, - какую цель преследует показатель, в том направлении и начинает действовать тенденция развития. Поэтому необходимо сочетание целевых и технологических показателей. Их несоответствие вызывает на практике противоречия в системе показателей [8, с.81].
Планирование и прогнозирование производительности труда в эргатических системах с помощью МЭРА позволяет достичь так называемого эффекта Эдила [9, с.147]: «прогнозы при известных условиях воздействуют на предсказываемые события, способствуя или препятствуя их осуществлению, так или иначе модифицируя их». Поэтому наилучшим является сочетание экстраполяционного прогноза производительности и программно-целевого моделирования критерия соответствия целевых, плановых и директивных показателей с фактически достигнутыми результатами.
Обсуждение проблемы критериев завершим следующей рекомендацией: «Когда проектируется и создается самолет, то его можно пустить в эксплуатацию тогда и только тогда, когда он будет полностью закончен. Иное дело - система моделей. Её можно и нужно начинать использовать уже тогда, когда закончены лишь некоторые составные части» [10, с.22]. Методология идентификации биотехнического закона это вполне позволяет.
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико - математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100с.
- Скурихин В.И., Шифрин В.Б., Дубровский В.В. Математическое моделирование /
В.И. Скурихин, В.Б. Шифрин, В.В. Дубровский. - Киев: Техника. 1983. -270 с. - Поляк, Б.Т. Введение в оптимизацию / Б.Т. Поляк. - М.: Наука, 1983. - 384 с.
- Пасхавер И.С., Яблочник А.Л. Общая теория статистики. Для программированного обучения / И.С. Пасхавер, А.Л. Яблочник. - М.: Финансы и статистика, 1983. - 432 с.
- Современный синтез критериев в задачах принятия решений. - М.: Радио и связь, 1992. - 120 с.
- Гойзман, Э.И. Моделирование производственных процессов на шахтах / Э.И. Гойзман. - М.: Недра, 1977. - 192 с.
- Олдак, П.Г. Равновесное природопользование и экономический рост / П.Г. Олдак. - ЭКО. - 1984. - № 8. - С.44-61
- Федулов А.А. Проблемы создания экономико-математических моделей в АСУНТ /
А.А. Федулов, В.Н. Растегаев. - М.: Информэлектро, 1980. - 78 с. - Елисеева И.И. Логика прикладного статистического анализа / И.И. Елисеева, В.О. Рукавишников. - М.: Финансы и статистика, 1982. - 192 с.
- Проектирование самолетов: Учебник. - 3-е изд., перераб. и дополн. - М.: Машиностроение, 1983. - 616 с.
Библиографическая ссылка
Мазуркин П.М. БИОТЕХНИЧЕСКИЙ ЗАКОН И КОНСТРУИРОВАНИЕ АДЕКВАТНЫХ МОДЕЛЕЙ // Успехи современного естествознания. 2009. № 9. С. 125-130;URL: https://natural-sciences.ru/ru/article/view?id=12867 (дата обращения: 04.03.2026).




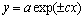 - закон Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого создана метод операторных исчислений
- закон Лапласа (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого создана метод операторных исчислений
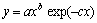 - биотехнический закон в упрощенной форме
- биотехнический закон в упрощенной форме
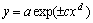 - закон экспоненциального роста или гибели, - по автору статьи
- закон экспоненциального роста или гибели, - по автору статьи
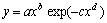 - биотехнический закон, предложенный проф. П.М. Мазуркиным
- биотехнический закон, предложенный проф. П.М. Мазуркиным