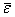 . Тогда чем ближе значение
. Тогда чем ближе значение По остаткам размах вариации (изменчивости) R по совокупности остатков равен
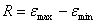 . (1)
. (1)
Среднее линейное отклонение ![]() составляет
составляет 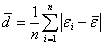 . (2)
. (2)
Дисперсия 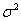 остатков с учетом малой выборки, когда
остатков с учетом малой выборки, когда ![]() ,будет равной
,будет равной
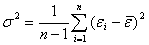 . (3)
. (3)
При ![]() впереди правой части уравнения (3) принимается отношение 1 / n . Среднее квадратичное отклонение остатков равно
впереди правой части уравнения (3) принимается отношение 1 / n . Среднее квадратичное отклонение остатков равно
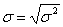 . (4)
. (4)
Коэффициент изменчивости (вариации) 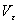 , дающий относительную оценку вариабельности остатков, определяется из выражения
, дающий относительную оценку вариабельности остатков, определяется из выражения
![]() . (5)
. (5)
Нормированное отклонение 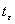 наблюдения определяется по формуле
наблюдения определяется по формуле
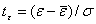 . (6)
. (6)
Принимается значение доверительного интервала -t - сигмальная единица. Например, пусть класс надежности расчетов принят B, то есть расчеты необходимы с малым риском. Поэтому [t]= 1,96. Для решения вопроса об исключения наблюдения и повторном поиске значений параметров модели по рекомендациям [2, с.260] необходимо выяснить сущность отклонения (так называемые «особые» точки, которые нами рассмотрены отдельно). Формально, если выполнено соотношение
![]() , (7)
, (7)
то такое наблюдение оставляется в статистической совокупности. При невыполнении условия (7) наблюдение исключается и поиск проводится по новому сеансу на ПЭВМ.
Асимметрия (скошенность) A S распределения остатков вычисляется по формуле
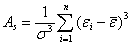 .(8)
.(8)
Если A S > 0 , то наблюдается правосторонняя асимметрия (вершина распределения расположена слева среднего значения), при условии A S < 0 - левосторонняя асимметрия. Чаще всего асимметрия выражает ненормальность распределения или наличие нескольких, сдвинутых вместе, распределений.
Эксцесс (островершинность) E будет равен
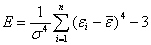 .(9)
.(9)
При островершинности E > 0 , то эксцесс положительный. Если E < 0 , то распределение остатков плосковершинное. По значениям t и σ определяются параметры функции кривой распределения. Уравнение нормированной (стандартной) плотности нормального распределения будет иметь вид [3, с.41]
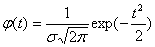 . (10)
. (10)
Другие виды распределения, как 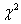 (хи - квадрат), Стьюдента ( t - распределение), биномиальное, логарифмическое, логнормальное и другие в технических исследованиях встречаются редко. В исследованиях могут встречаться известные устойчивые законы распределения, а также их комбинации.
(хи - квадрат), Стьюдента ( t - распределение), биномиальное, логарифмическое, логнормальное и другие в технических исследованиях встречаются редко. В исследованиях могут встречаться известные устойчивые законы распределения, а также их комбинации.
Предельная ошибка выборки остатков вычисляется по формуле
![]() ,(11)
,(11)
из которой вычисляется допустимое значение n по формуле
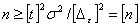 , (12)
, (12)
где допустимое значение t принимается по известным данным. Полученное значение n сравнивается со значением расчетного числа наблюдений.
Такие сложные расчеты необходимы при аппроксимации. В них нет необходимости при процедурах идентификации. Потому при поиске параметров модели можно воспользоваться еще более простыми формулами:
- ошибка среднеквадратичного отклонения 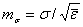 ;(13)
;(13)
- показатель точности наблюдений 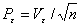 ;(1)
;(1)
- доверительные интервалы 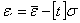 ;
;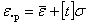 .(15)
.(15)
Адекватность модели. Для вычислений критериев адекватности необходимо определить:
- дисперсию теоретических значений показателя 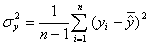 ,(16)
,(16)
где
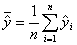 ; (17)
; (17)
- дисперсию фактических значений показателя
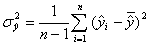 ; (18)
; (18)
- дисперсию остатков
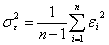 . (19)
. (19)
Значение дисперсии остатков можно также вычислять по правилу сложения дисперсией, поэтому
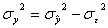 . (20)
. (20)
Для измерения тесноты связи принимается коэффициент детерминации B yx , равный [3, с.102]
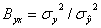 .(21)
.(21)
Чем ближе 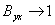 , то тем больше совпадают теоретические и фактические выходные результаты. Мера неопределенности регрессии, то есть влияние «необъясненной» дисперсии
, то тем больше совпадают теоретические и фактические выходные результаты. Мера неопределенности регрессии, то есть влияние «необъясненной» дисперсии 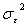 , определится из выражения
, определится из выражения
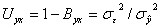 . (22)
. (22)
Исправленный коэффициент детерминации B * yx определится из формулы [3, с.108]
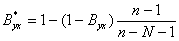 . (23)
. (23)
С вероятностью 1 - α , где α - уровень значимости по табл. 2, коэффициент детерминации проверяется по критерию Фишера [3, с.202]
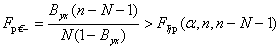 . (24)
. (24)
Существенность дисперсионной связи вычисляется по критерию Фишера [25, с.33] по формуле
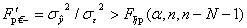 , (25)
, (25)
где 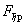 - табличное значение критерия Фишера, n - число наблюдений, N - число параметров модели. Регрессионная модель считается работоспособной, если
- табличное значение критерия Фишера, n - число наблюдений, N - число параметров модели. Регрессионная модель считается работоспособной, если 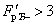 [4, с.34]. По критерию Фишера
[4, с.34]. По критерию Фишера 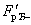 сравниваются несколько альтернативных регрессионных моделей, если таковые возникнут при обсуждении проблемы построения конструкций моделей (способами аппроксимации). Например, лучше обычная или нормализованная формы модели, предпочтительнее арифметические или алгебраические оперативные константы.
сравниваются несколько альтернативных регрессионных моделей, если таковые возникнут при обсуждении проблемы построения конструкций моделей (способами аппроксимации). Например, лучше обычная или нормализованная формы модели, предпочтительнее арифметические или алгебраические оперативные константы.
Автоматический поиск параметров модели. Для оценки сходимости и адекватности модели автоматического поиска параметров модели целесообразно вычислять статистические показатели, соотнесенные к выходным результатам объекта исследования:
- сумма квадратов отклонений
![]() ;(26)
;(26)
- среднеквадратичное отклонение
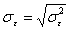 ; (27)
; (27)
- ошибка среднеквадратичного отклонения
![]() ; (28)
; (28)
- коэффициент изменчивости
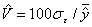 ; (29)
; (29)
- показатель точности
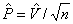 ;(30)
;(30)
- относительное отклонение выходных результатов
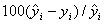 ; (31)
; (31)
- среднее относительное отклонение выходных результатов
![]() . (32)
. (32)
Максимальное отклонение Δ max выбирается из значений (31) по абсолютной величине из множества | Δ i | .
Сравнение моделей по критериям адекватности. Все существующие методы анализа адекватности моделей статистическим выборкам предполагают однородность экспериментов, включенных в одно множество. При этом классическая статистика четко предполагает только наличие закона нормального распределения.
Однако полезно сравнить предложенный метод оценки адекватности по максимальной относительной погрешности с известными методами, в частности, с методом Фишера. Он наиболее распространен в сельскохозяйственной и инженерно-экологической науке.
Средняя относительная погрешность по остаткам от модели. Поэтому наиболее простому известному способу суммируются все отношения остатков ξ i по модулю (без учета знаков, то есть | ξ i | ) к фактическим значениям изучаемого показателя . В результате исключается проблема сравнимости моделей и одновременно «проклятие» размерности показателя 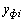 . Затем вычисляется результат как сумма ∑ и она делится на число n членов (наблюдений) статистической выборки.
. Затем вычисляется результат как сумма ∑ и она делится на число n членов (наблюдений) статистической выборки.
Тогда получается сопоставимый для любых статистических моделей, полученных аппроксимацией произвольных формул или идентификацией устойчивых законов и закономерностей критерий адекватности - средняя относительная погрешность 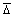 (%)
(%)
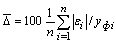 . (33)
. (33)
Однако любая средняя арифметическая величина относится к нормальному закону распределения, поэтому не применима к неоднородным статистическим выборкам, каждый член которых имеет собственную индивидуальность. Поэтому по формуле (33) можно получить одно и то же значение относительной погрешности для нескольких выборок, имеющих различные друг от друга законы распределения. При этом размах 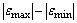 может быть сильно различающимся. Поэтому лучше всего определять относительную погрешность по формуле (33), а затем выделить
может быть сильно различающимся. Поэтому лучше всего определять относительную погрешность по формуле (33), а затем выделить 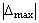 . Тогда получается, что требование адекватности по максимальной относительной погрешности в несколько раз (равное отношению
. Тогда получается, что требование адекватности по максимальной относительной погрешности в несколько раз (равное отношению 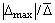 ) строже по сравнению с известным методом.
) строже по сравнению с известным методом.
Средняя квадратичная погрешность. Чтобы исключить влияние знаков, было придумано возвести в квадрат остатки, то есть получить выборку в виде ряда ξ 2 .
Но вначале придется определить среднее арифметическое от всех значений изучаемого показателя, то есть применить формулу для нормального распределения случайных событий
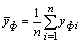 . (34)
. (34)
Среднеарифметического объекта в природе физически не существует. Поэтому эта физическая величина весьма условная, придуманная математиками для сравнения статистических выборок друг с другом. Однако много существует однородных выборок с членами, равными по сущности неотличительных признаков, у которых с различным размахом ![]() может оказаться одинаковое значение среднего арифметического.
может оказаться одинаковое значение среднего арифметического.
Таким образом, уже изначально ясно, что метод среднеквадратичного отклонения (погрешности) не примелем для выявления адекватности идентификации закономерностей. Однако до сих пор применяют для выявления адекватности аппроксимированных уравнений, не имеющих содержательного смысла по параметрам и отдельным составляющим, формулу (при этом к методу наименьших квадратов не относится)
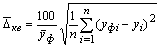 . (35)
. (35)
F-критерий Фишера. Этот показатель адекватности относится к дисперсионному анализу. Он оказывает статистическую значимость уравнения регрессии (в нашем случае статистически устойчивой закономерности, построенной на основе устойчивых законов) в целом. Анализ адекватности модели выполняется сравнением фактического F Ф и табличного (критического) F значений критерия Фишера.
При этом фактическое значение критерия вычисляется, с использованием дисперсий на одну степень свободы, по формуле
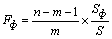 ,(36)
,(36)
где n - число членов (единиц) статистической совокупности, шт., m - количество объясняющих факторов в уравнении (модели), шт. S Ф - факторная дисперсия (по размерности изучаемого показателя), S- остаточная от модели дисперсия (по размерности показателя).
В формуле (36) обращает внимание тот факт, что по выражению в числителе n - m - 1 количество объясняющих переменных должно соответствовать условию 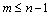 .
.
Многие примеры идентификации показали, что это условие по Фишеру при использовании устойчивых законов необязательное, поэтому количество одновременно учитываемых факторов может быть и больше числа наблюдений (например. 14 факторов при 10 сложных по количеству влияющих факторов наблюдениях).
При этом было замечено, что конструктивная связь между факторами требует наименьшего количества параметров модели. С переходом на мультиколлениарные связи потребуется большее количество параметров модели, а при аддитивной связи будет наблюдаться наибольшее количестве параметров у искомой статистической закономерности.
Факторная дисперсия, то есть сумма квадратов отклонений фактических значений показателя от их среднеарифметического по формуле (7.25), вычисляется по уравнению
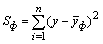 , (37)
, (37)
где y - расчетное по модели значение изучаемого показателя, 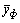 - среднее арифметическое у фактических значений показателя. Остаточная дисперсия, то есть сумма квадратов отклонений по остаткам
- среднее арифметическое у фактических значений показателя. Остаточная дисперсия, то есть сумма квадратов отклонений по остаткам 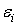 , определяется по выражению
, определяется по выражению
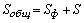 .(38)
.(38)
Общая вариация (дисперсия) результата определяется по формуле
![]() . (39)
. (39)
Примеры сравнения. Для сопоставления различных критериев адекватности используем табличные данные по трем гидрометрическим створам и пяти показателям свойств у 18 проб травы [5]. Табличное критическое значение критерия Фишера равно 3,68 для всех пяти двухфакторных моделей при степенях свободы для расчета фактического критерия Фишера k 1 = n - m - 1 = 18 - 2 - 1 = 15 и при этом для двух учтенных факторов k 2 = m = 2 .
Удельная масса сырой травы. В табл. 1 приведены результаты расчетов различных критериев адекватности одной и той же модели. Предлагаемый нами критерий адекватности приведен в первом столбце. Он не требует никаких дополнительных расчетов и прост в применении тем, что нужно просмотреть относительную погрешность по всем строкам и выбрать максимальную из значений погрешности, обозначив как Δ max (%).
Поверхность отклика на рис. 1 сложна и она в среднем характеризуется статистической моделью вида
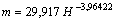
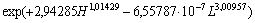 . (39)
. (39)
На площадке № 7 показатель по формуле (39) получил наибольшую погрешность Δ max = 54,24% . Относительную погрешность Δ = 38,21% получила травяная проба на пробной площадке № 15. Средняя относительная погрешность ![]() (%) требует небольших вычислений. Вначале определяется сумма погрешностей по модулю (второй столбец табл. 1), а затем вычисляется средняя погрешность.
(%) требует небольших вычислений. Вначале определяется сумма погрешностей по модулю (второй столбец табл. 1), а затем вычисляется средняя погрешность.
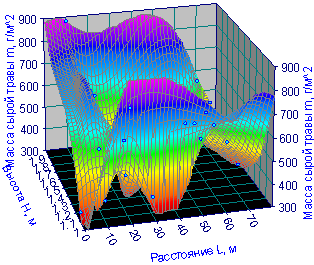
Рис. 1. Поверхность отклика массы срезанной травы в среднем на трех створах реки Ировка
Таким образом, формула (39) получила по предложенному нами критерию адекватности Δ max для седьмой пробной площадки и при этом второй статистический показатель 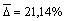 . Средняя квадратичная погрешность равна
. Средняя квадратичная погрешность равна 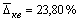 . Тогда получается, что максимальная относительная погрешность больше средних величин соответственно в 54,24 / 21,14 ≈ 2,6 и 54,24 / 23,80 ≈ 2,3 раза.
. Тогда получается, что максимальная относительная погрешность больше средних величин соответственно в 54,24 / 21,14 ≈ 2,6 и 54,24 / 23,80 ≈ 2,3 раза.
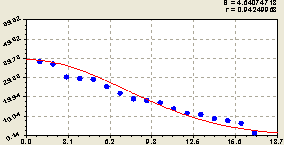
Распределение погрешностей только частично подчиняется нормальному закону Гаусса-Лапласа. Однако биотехнический закон адекватнее. Например, нормальное и ранговое распределения значений из второго столбца табл. 1 определяются формулами:
- закон нормального распределения погрешностей по модулю
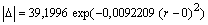 ;(40)
;(40)
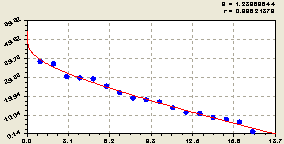
- распределение по биотехническому закону проф. П.М. Мазуркина
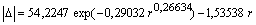 . (41)
. (41)
Сравнение показывает, что нормальное распределение по закону Гаусса-Лапласа при условии (здесь этот закон приводится напрямую по параметрам) относительно оси ординат биотехнический закон (закон гибели как его частный случай) имеет более высокое значение коэффициента корреляции 0,9962 > 0,9425 (рис. 2).
Таблица 1. Критерии адекватности закономерности (39) массы проб сырой травы
|
№ п/п |
Δ max, % |
|
Среднее квадратичное |
F -критерий Фишера F Ф =3,20<3,68 |
||
|
|
|
S Ф |
S |
|||
|
1 |
16,91 |
16,91 |
880 |
22141,4 |
48796,8 |
22141,4 |
|
2 |
8,76 |
8,76 |
580 |
2580,6 |
14520,3 |
2580,6 |
|
3 |
30,26 |
30,26 |
420 |
16154,4 |
1354,2 |
16154,4 |
|
4 |
1,45 |
1,45 |
475 |
47,6 |
806,6 |
47,6 |
|
5 |
13,92 |
13,92 |
600 |
6972,3 |
38,4 |
6972,3 |
|
6 |
21,70 |
21,70 |
440 |
9120,3 |
635,0 |
9120,3 |
|
7 |
54,24 |
54,24 |
340 |
34003,4 |
198,8 |
34003,4 |
|
8 |
37,08 |
37,08 |
390 |
20909,2 |
590,5 |
20909,2 |
|
9 |
29,60 |
29,60 |
780 |
53314,8 |
1505,4 |
53314,8 |
|
10 |
29,05 |
29,05 |
630 |
33489,0 |
4006,9 |
33489,0 |
|
11 |
19,04 |
19,04 |
490 |
8704,9 |
12905,0 |
8704,9 |
|
12 |
6,52 |
6,52 |
315 |
506,3 |
20391,8 |
2756,3 |
13 |
11,42 |
11,42 |
565 |
4160,3 |
96,0 |
4160,3 |
|
14 |
10,91 |
10,91 |
460 |
2520,0 |
0,0 |
2520,0 |
|
15 |
38,21 |
38,21 |
380 |
21083,0 |
222,0 |
21083,0 |
|
16 |
25,28 |
25,28 |
595 |
22620,2 |
4316,5 |
22620,2 |
|
17 |
8,00 |
8,00 |
415 |
1102,2 |
3856,4 |
1102,2 |
|
18 |
18,26 |
18,26 |
430 |
6162,3 |
3,2 |
6162,3 |
|
Сумма |
380,61 |
9185 |
265592,0 |
114244,0 |
267842,1 |
|
|
Критерий |
21,15 |
510,3 |
23,80 |
|
|
|
Вроде бы асимметрия небольшая, но она имеет колоссальное креативное значение. Поэтому формула (39) может быть применена, то есть, не отброшена как статистически недостоверное, только из-за того, что её конструкция идентична конструкции моделей других показателей у свойств луговой травы. Однако уравнение с конкретными параметрами модели (39) не может быть использованы в различных технологических или иных расчетах.
|
|
|
|
а) |
б) |
Рис. 2. Графики нормального (а) и биотехнического (б) распределения ошибок
Результаты сравнительных расчетов приведены в табл. 2.
Полужирным шрифтом выделены наилучшие значения того или иного критериев адекватности. Заметим здесь, что эмпирическим путем в эконометрике достигнуто требование к средней погрешности ![]() эконометрической модели в 8,0%. Этот уровень вполне совпадает с погрешностью 8,81% табл. 2 для относительной влажности.
эконометрической модели в 8,0%. Этот уровень вполне совпадает с погрешностью 8,81% табл. 2 для относительной влажности.
Сравнение показало, что наипростейшим критерием адекватности и более точным по сущности идентифицируемых природных и природно-антропогенных явлений и процессов является статистический показатель Δ max - максимальная относительная погрешность (в процентах).
В заключение приведем слова Н. Винера [6, с.76]: «... современный аппарат малых выборок, как только он выходит за рамки простого подсчета своих собственных, специально определенных параметров и превращается в метод положительных статистических выводов для новых случаев, уже не внушает мне доверия, Исключение составляет случай, когда этот аппарат применяется статистиком, который явно знает или хотя бы неявно чувствует основные элементы динамики исследуемой ситуации».
Таблица 2. Критерии адекватности по моделям изменения показателей луговой травы
|
Параметр травы |
Δ max, % |
|
|
|
F Ф |
R 2 |
R |
|
m , г/м2 |
54.24 |
21.15 |
510.3 |
23.80 |
3.20 |
0.299 |
0.547 |
|
m c, г/м2 |
51.31 |
19.22 |
138.6 |
20.62 |
3.82 |
0.461 |
0.679 |
|
m в0, г/м2 |
59.87 |
22.95 |
364.2 |
26.26 |
3.12 |
0.294 |
0.542 |
|
W , % |
26.21 |
8.81 |
250.1 |
10.32 |
4.59 |
0.379 |
0.616 |
|
|
46.66 |
18.77 |
1.312 |
21.44 |
1.87 |
0.200 |
0.447 |
Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ
СПИСОК ЛИТЕРАТУРЫ:
- Мазуркин, П.М. Статистическое моделирование. Эвристико-математический подход / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2001. - 100с.
- Пасхавер, И.С. Общая теория статистики. Для программированного обучения /
И.С. Пасхавер, А.Л. Яблочник. М.: Финансы и статистика, 1983. - 432 с. - Фёрстер, Э. Методы корреляционного и регрессионного анализа: Руководство для экономистов / Э. Фёрстер, Б. Рёнц. - М.: Экономика и статистика, 1983. - 302 с.
- Елисеева, И.И. Логика прикладного статистического анализа / И.И. Елисеева, В.О. Рукавишников. - М.: Финансы и статистика, 1982. - 192 с.
- Мазуркин, П.М. Измерение продуктивности травяного покрова пойменного луга /
П.М. Мазуркин, С.И. Михайлова // Современные наукоемкие технологии: материалы заочной электронной конференции. - 2008. - № 7. - С.91-92. - Винер, Н. Кибернетика или управление и связь в животном и машине / Н. Винер. - 2-е изд. - М.: Наука, 1983. - 344 с.
Библиографическая ссылка
Мазуркин П.М. БИОТЕХНИЧЕСКИЙ ЗАКОН И АДЕКВАТНОСТЬ ГОТОВОЙ МОДЕЛИ // Успехи современного естествознания. 2009. № 9. С. 130-137;URL: https://natural-sciences.ru/ru/article/view?id=12868 (дата обращения: 04.03.2026).




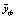
 , %
, %
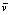 , г/(м2 ч)
, г/(м2 ч)