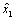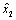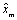Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Мазуркин П.М.

Статья в формате PDF

249 KB

Модель может идентифицироваться и по текущей информации в реальном режиме времени, но при этом процесс идентификации не должен превышать одной трети промежутка времени между получением каждой порции сведений. Однако и здесь на первом сеансе значения параметров искомой модели необходимо вычислить по прошлым данным, то есть необходим анализ некоторой предыстории явления или процесса. Последующие сеансы параметрической идентификации выполняются гораздо быстрее из-за использования готовых после первого сеанса моделей.

На рис. 1 приведены условные примеры аппроксимации (рис. 1а) и параметрической идентификации (рис. 1б).

В первом случае логарифмированием получаем вместо показательного закона 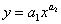  линейную модель  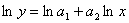. Во втором случае точная линеаризация невозможна. Исследователи пытаются практически решить эту задачу статистического моделирования с помощью уравнения  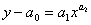 путем принятия ориентировочных значений a ₀ . Однако результат такого решения может оказаться некорректным. Тогда снова подбирают значение a ₀  до тех пор, пока график на рис. 1б не будет глазомерно максимально приближен к множеству экспериментальных данных.

Этот простейший пример неавтоматизированного выбора конструкции модели показывает, что необходим некоторый перебор вариантов значений a ₀ . Если принятое значение a ₀  удовлетворяет критериям сходимости и адекватности модели к фактическим данным, то он запоминается. Так шаг за шагом выполняется случайный поиск, в данном примере в неавтоматизированном режиме.

Многие статистические модели не поддаются линеаризации. Многофакторные модели практически всегда невозможно аппроксимировать. Вначале для понимания сущности математических конструктов строятся частные характеристические графики (без масштаба) бинарных отношений типа «фактор x _i  - показатель y ».

Рис. 1. Характеристические графики, построенные по множеству экспериментальных точек: а - модель, приводимая к линейному виду и, соответственно, поддающаяся апроксимации; б - модель, не приводимая (точно) к линейному виду и требующая параметрической идентификации; x, y- координаты экспериментальных точек

На рис. 2 показан условный пример построения составных моделей по какому-то бинарному отношению 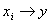 . По схеме на рис. 1а эксперт считает, что изменение  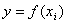 состоит из двух процессов. Причем он указывает математику-программисту (исходя из эвристик задачи), что оба этих процесса могут быть охарактеризованы показательными законами, то есть общая модель будет  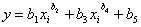 (здесь и далее мы произвольные параметры будем перенумеровывать, поэтому в отличие от параметров  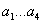биотехнического закона будем использовать, по возможности, другой символ).

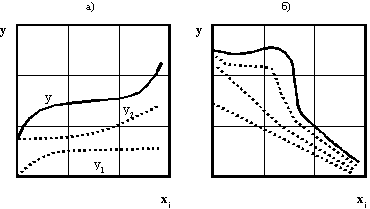
Рис. 2. Характеристические графики бинарных отношений xy, приводимые к составным конструкциям (модульным построением при использовании устойчивых законов) регрессионных моделей: а - сумма показательных функций; б - сумма линейной, экспоненциальной и логистической математических функций

Если известны интервалы изменения x ₁  и ориентировочно (по мысленным представлениям) можно указать на интервалы 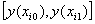 изменения показателя  (предварительных расчетов не требуется), то возможно указать для ПЭВМ (программы Eureka для малых выборок, ПЭК или CurveExpert-1.3 для матриц данных) значения b1...b5 . Пусть для нашего примера b ₅ = 2.5  (главное здесь угадать не значение числа, а только порядок,: если будет введено в ПЭВМ число 2500, то поиск будет затруднен, так как долгий путь машинного поиска предстоит до окончательного значения параметра, например, b ₅ =1.8364).

Исходные значения b ₁ и b ₃ угадать труднее, а для интенсивностей можно указать области нахождения числа: 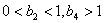. Если решается множество однотипных задач, то для второго и последующих примеров принятие исходных значений параметров идентифицируемой модели упрощается, так как значения параметров идентифицируемой модели принимаются по аналогии с первым примером.

Пусть задана матрица данных   , где знак « ^ » будем принимать для фактических значений. Эта матрица оформляется в виде табл. 1.

Таблица 1. Форма матрицы исходных данных

Матрица 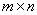 может быть полностью заполненной. Если имеются пустые клетки, то необходимо учитывать возможность исключения некоторых факторов и групп наблюдений в некоторых математических конструктах.

Далее строятся структурные модели, например, типа:

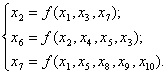    (1)

Такие структурные модели только указывают на зависимость одних факторов от других. Эксперт-специалист это обязан выполнить. Причем основным условием конструирования является структурная избыточность. Лучше, если конструкция каждой из составляющих математической модели будет избыточной, до полной формы. Так же желательно, если бинарные отношения будут записаны в усложненной форме, например, вместо формулы y = ax  следует использовать y = ax ^b или даже y = ax ^b exp (-cx) и т.п.

В системе структурных уравнений (1) левые части становятся показателями, то есть x ² → x ¹ , x ⁶ →  y ², x ⁷ → y ³ и т.д. Так выполняется разделение факторов на объясняющие переменные x _i  и показатели y _k . При факторном анализе структурные модели типа (1) не строятся, так как как будут известны модели всех бинарных отношений между отдельными факторами.

Мы ранее указывали, что множество y _k  можно свернуть в обобщенный критерий (или принять несколько общих критериев) оптимизации. Эта работа при идентификации не выполняется, поэтому в данной книге не рассматривается.

При однофакторном моделировании табл. 1 превращается в двухстолбцовую таблицу со столбцами x^  и y^ 

Свойства исходных данных. Для работы по методике МЭРА не требуется выполнять корреляционный и дисперсионный анализы. Причем общеизвестно, что существующие методы статистического моделирования исходят именно из допущения о нормальном законе распределения исходных данных.

На рис. 3 приведены практически возможные случаи распределения наблюдений в однофакторном эксперименте. Отсутствие влияния  x → y будет по схемам на рис. 3а,в описываться моделью типа 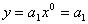 . При нормальном законе распределения (рис. 3а) получим  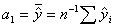, где 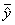 - среднее арифметическое фактических значений, n - общее число наблюдений.

На рис. 3б показано дискретное изменение x , когда при каждом значении x^  образуется статистическая частная выборка y^ , которая равномерно распределена одинаково для значений x^ . В итоге образуется линия регрессии по значениям y = f (x) . Эта линия равновероятно отстоит в пределах доверительных границ y^ ₁ и y^ ₂ . Очевидно, что такое распределение возможно аппроксимировать. Однако, как показали наши примеры, идентификация многофакторных моделей и здесь эффективнее.

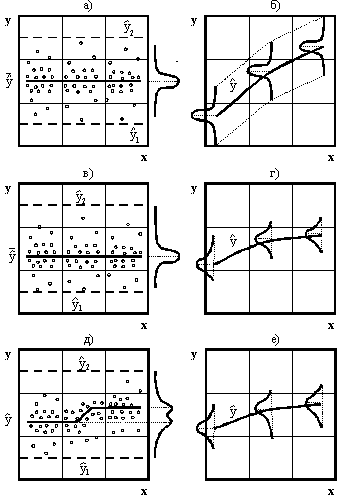
Рис. 3. Возможные случаи распределения повторностей наблюдения : а - случайные изменения x, y и нормальное распределение y; б - равномерно нормальные распределения y при дискретнозаданном изменении x (обычно планированием эксперимента); в - асимметрия нормального распределения y; г - равномерно асимметричное распределение выборок y при дискретных x; д - появление эксцесса у нормального распределения; е - случайные изменения асимметрии распределения

С отклонением законов распределения от нормального погрешность аппроксимации возрастает. По схеме на рис. 3в происходит значительная асимметрия исходных данных. Линия регрессии (рис. 3г) фактически проходит по «сгущенным» множествам экспериментальных точек, а аппроксимированная линия идет по среднеарифметическим значениям и поэтому отклоняется от сгущенностей наблюдений. Чем больше асимметрия, то тем существеннее разница между линией моды 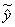  и линией среднеарифметической  .

Появление эксцесса (рис. 3д) может произойти из-за каких-то структурных сдвигов (например, включилось во времени влияние не учтенного фактора) или из-за резкого скачка погрешностей измерения. Вот почему рекомендуется эксперименты проводить быстро, не давая времени повлиять на ход процесса самого эксперимента. Однако управление временем эксперимента чаще всего возможно выполнить только в технических исследованиях.

Эксцесс появляется также от неучтенного порогового эффекта нелинейного скачкообразного влияния фактора (переход в новое качество, например от закона Гука к упруго-пластической деформации, от стабильности экономики к кризису и др.). В условиях производства это может быть изменение самоорганизации персонала и др. Способом идентификации объяснимые скачки (например, работа в праздничные дни и др.) вполне можно учесть и включить в виде отдельных математических конструктов.

На рис. 3е показано изменение линии регрессии при дискретных замерах и различных законах распределения исходных данных по отдельным выборкам. Методика МЭРА позволяет получить регрессионную модель, проходящую по вершинам различных типов распределений. Это означает, что вид частных законов распределения выборок не влияет на результат параметрической идентификации.

В лесном деле часты случаи со взаимно связными факторами, когда необходимы взаимно обратимые математические функции типа y = f (x) или x = φ (y) . Например, высота и диаметр дерева взаимосвязаны, а сама функциональная связность (прямая и обратная) зависит от параметров местообитания этого дерева.

На рис. 4 схематически показано, что в статистических выборках X^ ↔ y^  появляются так называемые зоны устойчивости исходных данных. При идентификации методами случайного поиска к ним стремится линия регрессии.

На рис. 4а показаны взаимные нормальные распределения неэкспериментальных данных, то есть данных, не зависящих от воли исследователя. Зона устойчивости крестообразной формы получается в виде двух прямых 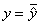 и 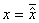. При этом центр устойчивости  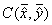превращается в точку.

По схеме на рис. 4б нет четкого проявления какого-то закона распределения. Предельными случаями становятся пуассоновское случайное распределение или регулярное (посадка деревьев в плантациях) размещение неэкспериментальных и экспериментальных точек [16]. Центра устойчивости здесь нет.

А зона случайного изменения 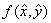 охватывает всю область точек. В этом случае моделирование становится бессмысленным процессом, так как можно провести бесчисленное множество кривых, от которых точки будут равноотстоящими по двум одинаковым частям множества исходных данных.

Рис. 4. Схемы, показывающие появление зон устойчивости исходных данных при случайных зависимостях x и y: а - нормальное распределение приводит к устойчивости в ориентациях xy и yx (вид "креста"); б - неустойчивая зона во всей области f(x,y); в - устойчивая сходимость зоны в центр C(x,y); г - сходимость зоны устойчивости по статистической информации в область линии моды C(x,y)

Если нет эвристической модели, а наблюдения выполнены без содержательного обоснования, то на практике чаще всего это происходит по многим причинам: а) неверно подобраны интервалы изменения x^ и y^ ; б) нет увязки между эвристикой и математикой; в) слишком малы интервалы изменения x^ и y^ и т.п.

На рис. 4в показан идеальный случай, когда зона устойчивости исходных данных сводится в центральную точку .Эта точка является генеральной средней арифметической величиной. Очевидно, что точка С может образоваться и при других законах распределения, а также при их различных сочетаниях.

Процесс параметрической идентификации очень быстро сходится к устойчивым значениям параметров модели. Причем небольшие изменения (оператором ПЭВМ) значений параметров модели не влияют, так как все же эти параметры модели сходятся к одному набору чисел.

В реальных явлениях и процессах этого не происходит. Поэтому, как показано на рис. 4г, появляется влияние эксцесса. В области точек  появляется зона устойчивости по модам или медианам. Для множества факторов это будет какое-то замкнутое пространство, внутри которого линия регрессии может колебаться из-за сочетаний различных значений параметров модели. Сходимость параметрической идентификации протекает дольше и исследователю иногда приходится выбирать какое-то сочетание значений по модели (1) по каким-то эвристическим соображениям. Такой случай стохастичности параметров модели появляется редко, да и то с увеличением количества параметров модели. Вычислительными экспериментами было установлено, что при числе факторов более 15 (m > 15 ) и числе переменных модели более 25 моделирование становится неустойчивым, то есть в этом случае трудно предсказуемым процессом.

Для преодоления этого явления и повышения устойчивости исходных данных необходимо моделировать комплекс формул, поочередно идентифицируя по матрице исходных данных каждую модель (2) в отдельности.

Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ

Библиографическая ссылка