- нити основы перемещаются в вертикальном направлении, разделяются в соответствии с рисунком переплетения и образуют зев;
- в образованный зев вносится уточная нить;
- проложенная в зеве уточная нить прибивается к опушке ткани;
- наработанная ткань постепенно отводится и наматывается на товарный валик, а основа перемещается в продольном направлении;
- основа сматывается с ткацкого навоя под определенным натяжением, необходимым для ведения технологического процесса.
Для исследования технологического процесса ткачества применяются различные методы. В последнее время в связи с развитием компьютерной техники стало возможным использование методов математического моделирования для исследования процессов в самых различных отраслях науки. Математическое моделирование представляет собой метод исследования объектов и процессов реального мира с помощью их приближенных описаний на языке математики - математических моделей. Для получения математических моделей можно использовать различные интерполяционные полиномы, например, полином Ньютона.
Анализ работ, посвященных математическому моделированию процесса ткачества, показал, что метод приближения функций с помощью полинома Ньютона ранее не использовался. Для получения математической модели, описывающей изменение натяжения нитей основы при выработке ткани на ткацком станке, необходимо выполнить следующие действия:
1) На технологическом оборудовании, установленном в ткацком производстве или в лабораторных условиях, с помощью контрольно-измерительных приборов получают диаграмму или осциллограмму натяжения нитей. На диаграмме или осциллограмме выделяют участок, после которого цикл натяжения нитей повторяется.
2) Для получения дискретной информации об исследуемом процессе разбивают диаграмму или осциллограмму натяжения нитей с выбранным постоянным шагом h изменения аргумента.
3) Определяют значения аргумента и функции в соответствии с выбранным постоянным шагом по экспериментальной диаграмме или осциллограмме натяжения нитей.
4) Для практического применения полинома Ньютона вводят новую безразмерную величину:
![]() ,
,
где ![]() - значение аргумента, занимающее начальное положение в таблице экспериментальных данных натяжения.
- значение аргумента, занимающее начальное положение в таблице экспериментальных данных натяжения.
5) Составляют диагональную таблицу разностей.
6) Подставляют значения разностей из таблицы разностей, в полином Ньютона, который имеет следующий вид, и получают искомую математическую модель:
Используя данный алгоритм, было получено несколько математических моделей с различным шагом интерполяции. Оценка эффективности полученных математических моделей производилась путем расчета относительной средней квадратической ошибки для всех значений аргумента хi по формуле
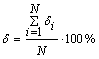 ,
,
где ![]() - относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
- относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
N- количество экспериментальных значений натяжения основных нитей.
![]() ,
,
где ![]() - абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
- абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
![]() ,
,
где ![]() - экспериментальные значения натяжения основных нитей, сН
- экспериментальные значения натяжения основных нитей, сН
![]() - теоретические значения натяжения основных нитей, вычисленные по математической модели, сН
- теоретические значения натяжения основных нитей, вычисленные по математической модели, сН
Математическое моделирование технологического процесса ткачества с помощью интерполяционного полинома Ньютона осуществлялось в программных оболочках Mathcad и Excel.
Для реализации поставленной цели по использованию интерполяционного полинома Ньютона для получения математической модели в лаборатории ткачества кафедры «Технология текстильного производства» Камышинского технологического института (филиал Волгоградского государственного технического университета) был проведен эксперимент по исследованию влияния заправочных параметров ткацкого станка СТБ-2-216 на физико-механические свойства ткани бязь. Результатом проведенного эксперимента явилось получение диаграммы зависимости натяжения нитей за оборот главного вала станка. Данная диаграмма в соответствии с вышеуказанным алгоритмом разбивалась на равные интервалы с шагом интерполяции h=5, 10, 15, 20, 30, 40, 60, 80, 120 град. После составления диагональных таблиц разностей и нахождения коэффициентов полинома было получено девять различных математических моделей.
В зависимости от выбранного шага математические модели имели следующие величины относительной средней квадратической ошибки для всех значений аргумента (см. табл.1).
Таблица 1. Показатели относительной средней квадратической ошибки в зависимости от шага интерполяции
|
Шаг интерполяции |
Величина относительной средней квадратической ошибки на интервале (0; 360 град.), % |
Величина относительной средней квадратической ошибки на интервале (80; 280 град.), % |
|
5 |
84,29 |
100,00 |
|
10 |
68,49 |
81,94 |
|
15 |
56,80 |
61,34 |
|
20 |
42,50 |
37,04 |
|
30 |
23,94 |
10,97 |
|
40 |
117,59 |
2,84 |
|
60 |
3,77 |
3,28 |
|
80 |
5,53 |
4,33 |
|
120 |
96,83 |
15,25 |
Из таблицы 1 видно, что наименьшую относительную среднюю квадратическую ошибку на интервале (80; 280 град.) имеет математическая модель с шагом интерполяции h=40 град. Кроме того, особенностью использования полинома Ньютона является то, что высокая точность достигается только для тех точек, которые расположены в середине интервала. Математическая модель, обладающая большей точностью для точек, близких к середине интервала, имеет следующий вид:

Выводы:
- Проанализированы методы приближения функций, которые могут применяться для описания технологических процессов ткацкого производства.
- На основе экспериментальных данных с использованием интерполяционного полинома Ньютона получены математические модели натяжения нитей основы при исследовании технологического процесса ткачества.
- Предложена методика оценки эффективности полученных математических моделей путем определения относительной средней квадратической ошибки.
- Разработан автоматизированный алгоритм по использованию метода приближения функций с применением интерполяционного полинома Ньютона для прогнозирования изменения натяжения на ткацком станке.
- Разработаны рекомендации по использованию полинома Ньютона при анализе натяжения в технологическом процессе ткачества.
Библиографическая ссылка
Назарова М.В., Березняк М.Г. ПОЛИНОМ НЬЮТОНА – КАК МЕТОД МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ НАТЯЖЕНИЯ НИТЕЙ В ТКАЧЕСТВЕ // Успехи современного естествознания. 2006. № 12. С. 80-81;URL: https://natural-sciences.ru/ru/article/view?id=13086 (дата обращения: 21.02.2026).



