В последнее время научный и практический интерес представляют вопросы прогнозирования процессов ткацкого производства. С этой целью применяют различные методы, позволяющие доводить решение сложных научных и инженерных задач, выдвигаемых практикой, до логического конца, то есть до математической модели, графика, диаграммы и т. д. Особое место среди методов математического моделирования занимают методы приближения функций. Эти методы в связи с большим объемом вычислений не нашли широкого применения. В их основе лежит замена одной функции f(x), зачастую представленной в виде таблицы экспериментальных значений, другой функцией g(x), вычисляемые значения которой и принимают за приближенные значения функции f.
Применение методов приближения функций позволяет решить следующие возникающие при исследовании технологических процессов проблемы:
- Функция f задана таблицей своих значений, а вычисления производятся в точках х, не совпадающих с табличными.
- Непосредственное вычисление значения y = f(x) связано с проведением сложных расчетов и приводит к значительным затратам машинного времени, которые могут оказаться неприемлемыми, если функция f вычисляется многократно.
- При заданном значении х значение f(x) может быть найдено из эксперимента. Такой способ в большинстве случаев нельзя использовать, так как найденные значения функции отличаются от истинных значений, поскольку заведомо содержат ошибки эксперимента.
Таким образом, применение методов приближения функций оправдано лишь тогда, когда значения g(x) вычисляются быстро и надежно, а погрешность приближения достаточно мала. С помощью методов приближения функций можно получить математическую модель исследуемого процесса и таким образом прогнозировать протекание технологического процесса на различном ткацком оборудовании.
Анализ работ, посвященных математическому моделированию процесса ткачества, показал, что метод приближения функций с помощью полинома Стирлинга ранее не использовался в виду сложности его применения из-за необходимости проведения громоздких вычислений. В настоящее время, в связи с быстрым развитием программного обеспечения, появилась возможность использовать интерполяционный полином Стирлинга для математического описания технологического процесса ткачества.
Сущность использования интерполяционного полинома Стирлинга для получения математической модели технологического процесса заключается в следующем.
1. На технологическом оборудовании, установленном в ткацком производстве или в лабораторных условиях, с помощью контрольно-измерительных приборов получают диаграмму или осциллограмму натяжения нитей. На диаграмме или осциллограмме выделяют участок, после которого характер изменения натяжения нитей повторяется.
2. Для получения дискретной информации об исследуемом процессе разбивают диаграмму или осциллограмму натяжения нитей с выбранным постоянным шагом h изменения аргумента.
3. Определяют по экспериментальной диаграмме или осциллограмме натяжения нитей значения аргумента и функции в соответствии с выбранным постоянным шагом.
4. Для практического применения полинома Стирлинга вводят новую безразмерную величину по формуле:
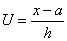 ,
,
где а - значение аргумента, занимающее центральное положение в таблице экспериментальных данных.
5. Составляют таблицу разностей для определения коэффициентов полиномa Стирлинга.
6. Подставляют значения найденных коэффициентов в полином Стирлинга и получают математическую модель.
В данной работе эффективность полученной математической модели оценивалась путем нахождения относительной средней квадратической ошибки ![]() по формуле:
по формуле:
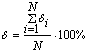 ,
,
где ![]() - относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
- относительная величина квадратической ошибки для каждого значения аргумента хi, , %;
N- количество экспериментальных значений натяжения основных нитей.
![]() ,
,
где ![]() - абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
- абсолютная средняя квадратическая ошибка для каждого значения аргумента хi;
![]() ,
,
где ![]() - экспериментальные значения натяжения основных нитей, сН
- экспериментальные значения натяжения основных нитей, сН
![]() - теоретические значения натяжения основных нитей, вычисленные по математической модели, сН
- теоретические значения натяжения основных нитей, вычисленные по математической модели, сН
Алгоритм оценки эффективности полученной математической модели с помощью полинома Стирлинга сводится к определению относительной средней квадратической ошибки для всех значений аргумента.
Для наглядного представления оценки эффективности полученной математической модели следует совместить экспериментальную и теоретическую кривую натяжения нитей.
Если относительная средняя квадратическая ошибка для всех значений аргумента значительна, то с целью получения более адекватной модели необходимо выбрать следующий шаг интерполяции и произвести расчет в соответствии с разработанным алгоритмом использования интерполяционного полинома Стирлинга для математического описания технологического процесса ткачества.
Использование данного алгоритма позволяет значительно сократить время, затрачиваемое исследователем на проведение многочисленных трудоемких вычислений при анализе натяжения в ткачестве.
Реализация процесса математического моделирования технологического процесса ткачества с помощью вышеуказанного метода приближения функций осуществлялась в среде программирования: Mathcad и Excel.
В ткачестве одним из важнейших параметров, определяющих протекание технологического процесса и качество ткани, является натяжение нитей основы на ткацком станке.
На базе лаборатории ткачества кафедры «Технология текстильного производства» Камышинского технологического института (филиал Волгоградского государственного технического университета) исследовалось влияние заправочных параметров ткацкого станка СТБ-2-216 на физико-механические свойства ткани бязь.
На ткацком станке в зоне «скало-ламельный прибор» был установлен тестер натяжения экспресс-диагностической установки фирмы «Метротекс», позволяющей измерять натяжение нитей при заданных технологических параметрах, а также получать диаграмму натяжения нитей.
Полученная экспериментальная диаграмма натяжения нитей исследовалась в соответствии с вышеописанным алгоритмом использования интерполяционного полинома Стирлинга для математического описания технологического процесса ткачества. Расчет производился по вышеуказанному алгоритму с шагом интерполяции h=5, 10, 15, 20, 30, 40, 60, 80, 120 град. Полученные математические модели имели следующую величину относительной средней квадратической ошибки, представленной в таблице 1.
Таблица 1. Показатели относительной средней квадратической ошибки в зависимости от шага интерполяции
|
Шаг интерполяции |
Величина относительной средней квадратической ошибки на интервале (0; 360 град.), % |
Величина относительной средней квадратической ошибки на интервале (80; 280 град.), % |
|
5 |
84,25 |
72,80 |
|
10 |
76,22 |
58,93 |
|
15 |
95,08 |
91,49 |
|
20 |
112,88 |
120,53 |
|
30 |
29,96 |
2,94 |
|
40 |
19,97 |
2,76 |
|
60 |
3,77 |
3,28 |
|
80 |
10,24 |
5,70 |
|
120 |
96,82 |
15,23 |
Таким образом, было установлено:
- при использовании полинома Стирлинга для исследования натяжения нитей основы на ткацком станке СТБ-2-216 целесообразно использовать шаг интерполяции h=40 град.
- применение интерполяционного полинома Стирлинга дает особую точность для точек, близких к середине интервала.
Выводы:
- Проведен анализ работ, посвященных математическому моделированию технологического процесса ткачества.
- Проанализированы методы получения математической модели для приближенного описания технологических процессов ткацкого производства.
- На основе экспериментальных данных с использованием интерполяционного полинома Стирлинга получены математические модели натяжения нитей основы при исследовании технологического процесса ткачества.
- Предложена методика оценки эффективности полученных математических моделей путем определения относительной средней квадратической ошибки.
- Разработан автоматизированный алгоритм по использованию метода приближения функций с применением интерполяционного полинома Стирлинга для прогнозирования изменения натяжения на ткацком станке.
- Разработаны рекомендации по использованию полинома Стирлинга при анализе натяжения в технологическом процессе ткачества.
Библиографическая ссылка
Назарова М.В., Березняк М.Г. ИССЛЕДОВАНИЕ ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ИНТЕРПОЛЯЦИОННОГО ПОЛИНОМА СТИРЛИНГА ДЛЯ ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРИ ОПИСАНИИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА ТКАЧЕСТВА // Успехи современного естествознания. 2006. № 12. С. 88-90;URL: https://natural-sciences.ru/ru/article/view?id=13123 (дата обращения: 13.03.2026).



