Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы

Верещагин И.А.

Обсуждены соотношения неопределенностей. Обнаружена близкодействующая структура октетного пространства. Рассмотрены приложения физических теорий.

Статья в формате PDF

159 KB

3.5. О СООТНОШЕНИИ НЕОПРЕДЕЛЕННОСТЕЙ

В классической квантовой механике это, в т.ч., соотношения неопределенностей Гейзенберга (СНГ): ΔtΔE ~ h, ΔsΔp_s ~ h. Как полагает А.Н. Малюта, в гиперкомплексных динамических системах (ГДС) для стационарных процессов имеют место соотношения неопределенностей в форме:

Δ₁...Δ_n = 1,                      (10)

где n - размерность ГДС, Δ_i = f(dφ_i, t) - i-я гиперкомплексная неопределенность. В простейшем случае Δ_i = k_iΔφ_i. Тогда

 Δφ₁Δφ₂.......Δφ_n = kC,                                    (11)

где С - константа ГДС, k = (k₁k₂...k_n) ^-1.

По аналогии с (**) можно построить семейство соотношений неопределенностей: Δ_iφ_ij = h_i, где i = 1...n, n - размерность Ф над Q, h_n - константа n-й теории. При i = 1 неопределенность нужно связывать с ошибками измерений, вычислений, алгоритмов и моделей - в рамках действительных чисел R (одна единица: 1). Вероятно, при i = 2 можно связать с некоммутирующими операторами квантовой механики состояний микрообъектов и их комплексных волновых функций над С (две единицы: 1, i). Возможно, при i = 3 - с неабелевой группой кватернионов над К (3 образующих единицы: 1, i, j). Допустимо, при i = 4 - с альтернативной алгеброй октав О (4 порождающих единицы: 1, i, j, E). И так далее, до обобщенно неассоциативных моноидов.

Однако в морфизме Q_n → (Ф_D над E_n) нет некоммутирующих операторов и ассоциаторов (как в приложениях теории при m´ = 0 нет следов октетного пространства, но физика - новая). Поэтому в физике Ф_D нет соотношений неопределенностей. Подобные соотношения могут появиться в приложениях, где приобретут вполне определенный физический смысл (в квантовой механике СНГ часто используется в детерминированных задачах). Это значит, что проблемы «скрытых параметров», поднятой вокруг квантово-механической парадигмы, в Ф_D нет, поскольку jusiV явлений нельзя «скрыть» волевым решением субъекта. Физика над Q имеет другой уровень феноменологии, нежели квантовая механика. Ф_D построена на базе достаточно общих аксиом, непосредственно опирающихся на простые опыты, и поэтому пресловутые «скрытые параметры» квантовой механики - в ней обычный материал для исследований. Поясним смысл замкнутости («совершенства») квантовой теории.

Известно, что замкнутость системы, в т.ч. теории, противоестественна и означает ее ограниченность. Известно также, что температура Т реликтового излучения R - величина статистически усредненная. Из соотношений : k_БТ ~ hν ~ m_eu²/2 находим: ν_R ~ (1 ÷ 6)10¹⁰ Гц. Поскольку опыт Пензиаса - Уилсона проводился с помощью радиотелескопа, то длина волны такого обнаруженного R будет c/ν_R ≈ λ_R ~ (1 ÷ 6) мм, где с - постоянная электромагнитной теории Максвелла, что совпадает с данными радиоастрономии и близко к пику интенсивности. Остальное из R радиотелескоп не улавливает. На этих длинах λ_R атмосфера Земли наиболее прозрачна для радиоволн: малы квантовые шумы и поглощение атмосферы [6]. То есть реликтовое излучение постоянно воздействует на элементарные частицы.

Из (Â) следует, что свободный электрон в результате типичного столкновения с реликтовым квантом в среднем приобретает скорость u_R ~ (0.5 ÷ 2)10⁴ м/с. Это и есть разброс средней «неопределенности» скорости Δ_Ru, то есть область, где находится математическое ожидание М[u] «случайной» скорости электрона в любом направлении внутри телесного угла 4π (ср. с шрёдингеровым дрожанием частиц). Действие случайных слагаемых ρ ∈ R неподконтрольно. То есть точности современных приборов пока не хватает для фиксации момента, места, характера соударения (прицельного расстояния, спина, эффективной массы) некоторого ρ из R с элементарной частицей. СНГ позволяет оценить среднестатистическое отклонение координаты: Δх ~ h/m_eu_R ≈ (3 ÷ 5)10^-8 м. Это комбинированная оценка: по R и СНГ. За период Т_R ≈ 1/ν_R электрон в среднем сместится на u_RТ_R ≈ Δх_R ~ (1 ÷ 2)10^-7 м. За четверть периода - так же, как в прежнем случае. Это оценка по R.

Но длина реликтовой радиоволны, воздействующей на микрообъект, λ_R >> Δх, что означает: 1) для электромагнитной радиации не выполняется СНГ (для оптических явлений на это указал В.А. Фок); 2) перманентное взаимодействие электрона с локальным вакуумом уменьшает разброс до Δ  ≤ λ_R /4 (для возможности влияния радиоволн на частицу); 3) формулы ε = hν, p = hk - лишь грубые аппроксимации сложных процессов передачи возмущений в электромагнитном вакууме (в частности, они линейны по h); 4) за время перехода t связанного электрона в атоме с одной «орбиты» на другую испускается или поглощается фотон с энергией Δε ~ h/τ, где Δε - разница энергии уровней, а возбуждение электромагнитной субстанции в оболочке атома делает виражи вокруг ядра многократно.

Действительно, в водородоподобном атоме, согласно СНГ, m_eΔuΔr ~ h, где Δr ~ (3 ÷ 6)10^-11 м (порядка боровского радиуса), откуда Δu ~ (0.5 ÷ 2)10⁺⁷ м/c. Из (m_eΔu²/2)Δτ ~ h найдем, что Δτ ~ (0.5 ÷ 1.5)10^-17 c (для света). Если Δτ ≈ τ, то λ ≈ сτ, и не покидая атом (не поглощаясь атомом) предфотон (постфотон) «обволакивает» ядро N = с/Δu ~ 40 ÷ 100 раз. В процессе удаления (сближения) с атомом рожденный (поглощенный) при переходе электрона фотон управляется не отдельным электроном, а атомом (всей системой). Поэтому при Δr_е ≈ Δr_р «неопределенность» Δu_p ≈ Δu_e , и N ~ 10⁵ ÷ 10⁶. Эта спираль удаляется от атома через время t - квант электромагнитного излучения не является монолитом, ограниченным размерами λ (кроме спиральности, есть цуг и предвестник). Отсюда получаем, что на своей длине волны фотон структурируется N-кратной спиралью, и этот фемтомеханизм обеспечивает взаимодействие реликтовых радиоволн со свободным электроном: λ_R /N ~ Δ⁺х, где Δ⁺х порядка размеров индуцированного из вакуума облака позитронов.

Таким образом, свободный электрон создает вокруг себя ореол (виртуальных) позитронов ⁺. Зарядовая ситуация антисимметрична атомной системе. Инертность электрона в море ⁺ примерно в m_e/m_p раз меньше, чем у атома Н (но он слабо связан). Поэтому радиофотон с энергией ε = hν_R (в принятом приближении) и длиной волны l_R в возбужденном электромагнитном вакууме вокруг электрона ведет себя подобно фотону при смене состояний электрона в атоме. Аналогично для других микрообъектов - с вариациями для электрически нейтральных и бесспиновых частиц.

Эта качественная картина показывает, что при условии λ_R >> Δх взаимодействие между реликтовым фоном и элементарной частицей возможно: 1) вопреки теореме Котельникова (ввиду дифракции изменяется топология); 2) «внутри» СНГ и со «скрытыми параметрами»; 3) вопреки структуре квантов, определяемой по линейным формулам ε = hν, p = hk; 4) в согласии с СНГ, рассматриваемом не как запрет на точное определение физических величин, а как детерминирующий фактор, следующий из некоммутативности операторов. Ошибки и неопределенности нужно отнести не к «принципиальному» индетерминизму, а к возможностям физика.

Вывод 1. Никакого особенного «принципиального» смысла в СНГ нет, включая приписываемый квантово-механический индетерминизм. Все «неопределенности», в том числе дифракция микрообъектов, следуют из их взаимодействия с реликтовым фоном. Закономерно, что нет никаких СНГ «внутри» элементарных частиц - на это указывает вид волновых функций для свободной частицы и частицы в центрально-симметричном поле кулоновского типа, получаемый уже в рамках самой квантовой теории. «Внутри» корпускулы ее, корпускулы, нет - есть лишь сферический ореол «вероятностей» вокруг нее.

Вывод 2. Зависимость СНГ от конкретных взаимодействий квантов полей эквивалентна относительности неопределенностей. Естествоиспытатель вынужден выбирать между релятивизмом «принципиального» индетерминизма и индетерминизмом «принципиального» релятивизма (являющимся разновидностью агностицизма).

3.6. О ЯДРЕ ЭЛЕКТРОНА

Подобно мегаструктуре Метагалактики, градация структурных уровней обнаруживается вглубь материи. Применима та же, в сущности, формула

-lg ≈  ,                       (12)

дающая последовательность неоднородностей материи и пространства в микромире, что дает ряд (см): 10⁰, 10^-4, 10^-8, 10^-12, 10^-16, 10^-20... Это, соответственно, длина «волны» гравитационного реликта, длина когерентности куперовской пары и размер (органической) молекулы (кристалла Н_2nO_n), порядка радиуса первой боровской орбиты (размер простейшего атома), примерно - комптоновская длина волны электрона, «размеры» ядра протона, кварки в «мешке» (?)...

Электрон как составляющая Метагалактики с ее lg R ≈ 28 подвержен воздействию стохастической электромагнитной волны с lg λ ≈ 28. Это дает оценку минимальной скорости электрона: lg u ≈ - 8 и его характерной неоднородности: lg r ≈ -20.

3.7. НЕСТАНДАРТНАЯ ПАМЯТЬ ПРОСТРАНСТВА

Численный эксперимент реализован для движения пробного тела массы m_и вблизи центра с мощностью W. Обнаружение эффекта зависит от прицельного расстояния.

Если вблизи тела находится центры перекачки энергии, необратимых процессов, включая эмоциональные возбуждения (физика эндокринной системы), то возможны деформации пространства и времени. Для взаимодействия «точечной» массы с зоной возбуждения примем: H = + F(T), где F(T) - потенциал провремени; уравнения вида f({ξ_i}, t) =  берутся в двух калибровках: f = 1 (ортогональность новой силы к скорости и новой скорости к силе), f = 0 (параллельность соответствующих сил и скоростей). Если F(T) = wT, масса покоящегося центра велика и его гамильтониан H = m_иu² + wT, то при Ĥ = -h²Δ/2m_и + wT для R = R(x, y, z, t), T = T(x, y, z, t) после простых преобразований получим систему:

ΔТ = adiv R + bT + cT ², ΔR = a´rot R + b´  + c´TR,                    (13)

где a = 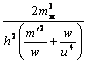, b = , c = a , a´ = ub´, b´ = , c´ = . Отсюда видно, что при некоторых комбинациях констант провремя Т и физическое пространство R³ в параметрических координатах «квантуются».

В «нулевом приближении» ΔТ = 0, ΔR = 0 при р_ц = 0, X_s = x_s(1 + ), T = 6bt(1 + ) обнаруживаем, что движение пробного тела вблизи возбужденного центра происходит по огибающим траекториям, а при столкновении с определенным прицельным расстоянием частица сначала от центра отражается вспять, а затем продолжает движение в том же заданном направлении, обогнув источник w (ср. с искривлением лучей света вблизи Солнца).

3.8. ПАДЕНИЕ ТЕЛА В ПОЛЕ ТЯЖЕСТИ

Интересен случай движения тела в однородном постоянном поле тяжести вблизи поверхности Земли. Провремя является линейной функцией от параметра t, а потенциал провремени принят равным нулю. В первом приближении по 1/u при Ĥ = -h²Δ/2m_и + m_гпgz, H = р²/2m_и + m_гпgz в квазиклассическом варианте F(T) = 0 получаем систему:

, , s = 1, 2, 3,     (14)

которая для f(p²) = Ap² + B, где А, В - константы, переходит в систему:

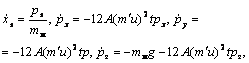    (15)

которая при А > 0,  > 0 описывает потерю кинетической энергии тела в поле тяжести. На уровне субполей этот эффект ведет к «покраснению» фотонов. При падении в силовом поле определенные комбинации констант g, A, h, u,  приводят к эффекту «гравитационной плоскости», по достижении которой тело останавливается.

Только благодаря фону фрактального пространства О (инвариантным по действию группы SO₂ струнам Лапласа) «кинетическая энергия» имеет смысл, а физика явлений зависит от размерности постулируемого пространства. Например, спиновая степень свободы - это проекция вращения в 4-мире на 3-вращение; в свою очередь, 3-вращение проецируется на оси координат в 3-мире. Постулат размерности пространства n < ∞, n ∈ N, всегда ограничивает : 1) своей конечностью; 2) целочисленностью. В физике актуален вопрос о компактифицированных измерениях.

Во втором приближении по 1/u² получаем для достаточно малых масс:

    (16)

откуда «мощность» W =  при f = 1 + o(p²) можно исключить.

В третьем приближении для Т = 6te(x, y, z) исследуется система:

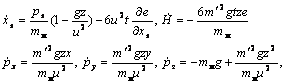(17)

из которой при малости mod (1 - e) можно исключить W = .

Если е = Аz² + B, где А, В - константы, то при начальных условиях р_х ≠ 0, p_y = p_z = 0 прослеживается эффект «тюльпан»: торможения частицы на некоторой высоте и плавный переход вертикальных колебаний в горизонтальные. Сложное падение тела вместо общепринятого движения по параболе связано с эффектами: 1) в заданных энергетических пределах - квантово-механическими; 2) структурных изменений пространства в больших полях гравитации; 3) совместной генерации пространства частицей и сильной гравитацией на микрорасстояниях. Анализ причин остановки частицы при ее приближении к центру тяготения, исследование связи данного эффекта с «гравитационным радиусом» позволяют предсказать отсутствие в природе так называемого гравитационного коллапса. Движение по многолистной траектории в случае падения в центр притяжения отмечено в [3]: пробная масса вблизи сферы Шварцшильда испытывает вертикальные пульсации в бесконечносвязном пространстве, каждая осцилляция происходит в новом листе (продолжая «падение»).

3.9. ПОДЪЕМНАЯ СИЛА В Q-МЕХАНИКЕ

Построим тернарную алгебру Q_A с умножением |(a, b, c) = [(ab)c - a(bc)]/2, где ассоциатор состоит из последовательно бинарных операций. С помощью тернарной алгебры над Q можно вычислять величины, определяющие инертные свойства вещества, память системы, время ее релаксации. Ассоциатор некоммутативен и несет информацию о степени необратимости системы.

В О произведение zyx = x´ можно разбить на два этапа: А[z]y = y´, A[y´]x = x´, где А - матрица, сигнатура которой определяется таблицей умножения термов q и w. Тогда (z, y, x) = {A[z](A[y]x) - A[A[z]y]x}/2. При y = z ассоциатор равен нулю (альтернативность). В k-компоненте ассоциатора нет «параллельных» членов, т.е. слагаемых с одинаковыми индексами сомножителей. Тернарная алгебра задается на новом умножении матриц с условиями:

А) (a_i, b_j, c_k) = 0 при (i j k) (i = j j = k k = i);

B) (a, b, c) = 0 при a = b b = c, а также

С) (a_i, b_j, c_k)_m = 0, если (i = m j = m k = m) m = 0;

D) (a_i, b_j, c_k)_m = 2f_ijkm(A²),

где f - функция, определяемая двойным преобразованием матрицы А в сигнатуре октав. Тем самым показано, что тернарная О-алгебра антикоммутативна и неабелева группа G(O, , ху, х^-1, 1) имеет представление, задаваемое матрицей А.

В О_А сила, противодействующая силе тяжести, записывается в форме F_z ~ ассоциатор₇, где знак «~» обязан отсутствию констант размерности:

F_z /2 ~ + z₆(- y₃x₂ + y₂x₃ - y₅x₄ + y₄x₅) - z₅(+ y₃x₁ - y₁x₃ - y₆x₄ + y₄x₆) -

 - z₄(- y₂x₁ + y₁x₂ + y₆x₅ - y₅x₆) + z₃(+ y₅x₁ + y₆x₂ - y₁x₅ - y₂x₆) +

 + z₂(- y₄x₁ - y₆x₃ + y₁x₄ - y₃x₆) - z₁(- y₄x₂ + y₅x₃ + y₂x₄ - y₃x₅).

Если x₁ = x₂ = x₃ = y₁ = y₂ = y₃ = 0, а также x₄ = y₄ = 0, то F_z ~ 2z₄(y₅x₆ - y₆x₅). Здесь переменные с n = 1, 2, 3 соответствуют декартовым координатам, с n = 4 - энергии, с n = 5, 6, 7 - проекциям импульсов тел или их составляющих элементов.

В центральном гравитационном поле система уравнений биоктетной механики для тела, обладающего собственным моментом и его прецессией, содержит нестандартные решения. Рассмотрим простейший случай: сечение Т = 0, сохраняющиеся энергию и функции M, F, а также H = + m_гпgz + m² + f ², где m - момент, f - момент силы, и соответствующие операторы. Тогда система примет вид:

 = (grad _p H - Ĥp) + (grad _m M - m) - (grad _f F - f),

 = - (grad H - Ĥr) +(grad _m F - m) + (grad _f M - f),

 = - (grad M - r) -(grad _p F - p) - (grad _f H - Ĥf),

 = (grad F - r) - (grad _p M - р) + (grad _m H - Ĥm).                                                              (18)

Начальные условия задачи Коши определяются видом терма М (в частности, при р_х ≠ 0). Для случая вертикальной прецессии горизонтального момента, вертикального момента и вертикального момента силы решения указывают на присутствие подъемной силы. Реализованные комбинации переменных позволяют сделать вывод о нестандартном поведении тела в анизотропной среде.

Вариант Т = kx²/2 в линейном приближении упругих свойств пространства Q для тех же вариаций начальных условий показывает, что сначала тело падает не по параболе, а затем уходит вверх на бесконечность.

3.10. ВОЗДЕЙСТВИЕ НА ПРОСТРАНСТВО И ВРЕМЯ

Система уравнений (11) в случае ΔТ = 0, ΔR = 0 при р_ц = 0, X_s = x_s(1 + ), T = 6bt(1 + ), но в приближении 1/r³ описывает деформации физического пространства и провремени:

g(r, v, t) = 1 +  - ,

,

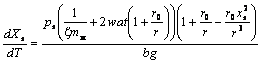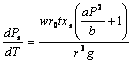
Происходит отталкивание пробного тела от источника w независимо от величины и направления начального импульса. На больших расстояниях, когда членами с 1/r³ можно пренебречь, моделируется рассеяние на w. Ситуация напоминает классическую, однако возможен финал а ля Броун.

Таким образом, механическое проникновение в микропространство элементарных частиц невозможно, если они испытывают необратимое внутреннее движение. Для поисков возможностей «расщепления» частиц необходимо искать электромагнитное, спиновое, «цветное» и т.д. расслоения их внутреннего пространства-времени. Данное явление - копия с рассеяния материи из очагов рождения и его следствие.

3.10. МИКРОЭНТРОПИИ

В пространстве кватернионов К операторный терм  где величины s, v, t, p соответствуют энтропии S, объему V, температуре Т, давлению Р, соответственно. Предметный терм S = εS + iV + jT + kP, где первая пара слагаемых - экстенсивные величины, вторая - интенсивные, k = ij. То есть запись произведена с учетом симметрии как двух пар {S, V} и {T, P}, так и двух пар {ε, i} и {εj, εij}. Коэффициенты размерности для краткости опущены.

Умножение в формуле  приводит к уравнениям:

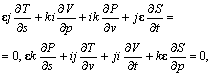
где числа i, j, k - единицы кватернионов, а число ε - при энтропии S и операторе ∂/∂s - имеет таблицу умножения, определяемую правилами:

ε² = 3, εi = i, εj = j, εk = k, iε = -i, jε = -j, kε = -k.

Тем самым из системы уравнений устраняется первое уравнение, и она приобретает стандартный термодинамический смысл:

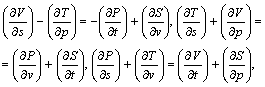
где второе уравнение - дополнительное, а четыре уравнения Максвелла содержатся в первом и третьем уравнениях, если продолжить их равенством нулю (то есть полученная система уравнений - более общая).

Левое и правое умножения e на гиперкомплексные единицы антикоммутируют, что означает: единица e той же природы, что и числа q Î K, но действует «вдоль» q, меняя лишь «направление» микрокручения. Первое правило позволяет ввести таблицу умножения для внутренних чисел энтропийной единицы, воспользовавшись аналогией с К и используя формулу для количества степеней свободы в V₃: , i = 0 ... 3, где степень свободы σ_о означает движение в монаде, а σ₃ - кручение пространства в целом, s₁ - количество степеней свободы прямолинейного движения, σ₂ - количество степеней свободы вращения в плоскости. В пространстве V_n количество степеней свободы прямолинейного движения есть число , количество степеней свободы вращений в плоскости есть число . Остальные степени свободы, кроме случаев  и , характеризуют множество сложных вращений в подпространствах v_m, m = 3 ... n - 1. За исключением монады μ(0), только в V₃ независимых вращений столько же, сколько независимых одномерных прямолинейных движений.

Если ε = ω + ε₁ + ε₂ + ε₃, то квадраты двойственных чисел = 1, i = 1 ... 3, а дуальное число ω таково, что ω² = 0. Тогда таблица для числа e имеет вид, представленный таблицей. Реальная часть таблицы Sp (ε²) = 3.

Таблица.

Таким образом, выявлена симметрия относительно «водораздела» "скрытые измерения - проявленные измерения": ε = {ω, ε₁, ε₂, ε₃} ↔ q = {i, j, k, e}.

Продолжая аналогию со степенями свободы в V₃ и имея в виду запись системы единиц в алгебре октав, можно заключить, что провремя имманентно самодвижению пространства V₃ в целом и имеет «двойника» в качестве монады w, символизирующей рождение «компактифицированных» степеней свободы ε₁, ε₂, ε₃ из эфира. Поскольку, как можно показать на примере состояния «электрический заряд», обратимость микросостояний недостижима в обозримом и необозримом будущем, открытые измерения характеризуют сущность провремени, которое в макромире имеет те или иные формы симметрии относительно отражения t → -t. Сам процесс генерации трех скрытых микросостояний провремени «точкой» эфира ω из Ω ⊂ Σ также необратим.

Расширение формализма физической теории над Q возможно не только вводом двойственного числа UU = 1 (или Е ² = 1) для единичной гиперсферы и дуального числа  (или Ω ² = 0) для получения уравнений стандартной гиперкомплексной физики, в частности над телом октав, но и вводом дополнительных гиперкомплексных чисел для описания физической ситуации в компактифицированных измерениях, близких к состоянию ω. В этом заключается количественная форма симметрии скрытых, генерирующих из себя иное микросостояний компактифицированных миров и проявленной, рожденной, антропогенной вселенной. Формально данная симметрия может быть записана в виде разложения числа е ≡ Df. <1> из так называемых макроскопических ГКС (сомножителя при провремени) на составляющие e с введенной выше таблицей умножения. В связи с вводом числа e аксиоматика октетной термодинамики может быть уточнена и расширена. Система гиперкомплексных чисел I | I ² = -1 , E | E ² = 1, Ω | Ω² = 0 дополняется системой гиперкомплексных чисел ε | Re (ε²) = 3, ω | ω² = 0, ε_i | ε_iε_i = 1, i = 1 ... 3, и, далее, таблицей умножения энтропийной единицы ε = ω + ε₁ + ε₂ + ε₃.

Однако в микромире «квант энтропии», количественно равный постоянной Больцмана k_Б, определяется не совсем точно. Например, неопределенность температуры в формуле dS =   в масштабах элементарных частиц ввиду некорректности определения термодинамических свойств системы из-за малого числа корпускул выражается отношением:  

где U - энергия взаимодействия, возбуждения, N - число частиц в системе. Для атома кислорода N = 16, и  ~ 0.2. Если N = 8 и U ~ 80 МэВ, то погрешность  ~ 0.7.

Экстраполяция понятия энтропии в мир элементарных частиц требует известной осторожности. Формула вида Е ~ k_БТ применима для молекул, размеры и области взаимодействия которых много больше размеров нуклонов и их ядер, несоизмеримы с подобными областями для элементарных частиц. Те же выводы можно распространить на закон Стефана - Больцмана. В недрах звезд, для изучения элементарных частиц и Метагалактики термодинамика нуждается в кардинальном уточнении и развитии. В этих областях познания материя существенно неравновесна, материальные системы открыты и их описание требует нелинейных математических уравнений.

В вершинах кристаллов возникают новые степени свободы. Проекции в V₃ скрытых состояний микроэнтропии необратимо взаимодействуют с окружающим фоном, в том числе увлекаются им. Кристаллы всех типов производят энтропию в своих характерных микрообластях, что проявляется как генерация спиновых, электромагнитных и других волн, интенсивность которых больше, чем интенсивность входящего излучения из окружающего пространства. Идеальный газ можно рассматривать как множество 0-мерных кристаллов. Значит, идеальный газ, кроме обычного расширения в разреженные среды, производит энтропию обращением компактифицированных состояний своих корпускул - в проявленные. Температура окружающей среды падает, поскольку тепло переходит в новые степени свободы. Эффект самопроизвольного понижения температуры изолированной, замкнутой термодинамической системы в фиксированном объеме кристаллического тела должен сопровождаться падением давления - согласно уравнению состояния идеального газа. С другой стороны, с возникновением новых степеней свободы макропространства давление в замкнутом объеме должно возрастать. Характер поведения термодинамических величин, определяющих состояние кристаллического вещества, может наблюдаться в достаточно точных опытах. Это позволит внести коррекции в определения термодинамических величин и таких понятий, как идеальный газ и изолированная система.

СПИСОК ЛИТЕРАТУРЫ

1. Верещагин И.А. Постэфирная гиперсимметрия Вселенной. Часть 1 // Успехи современного естествознания. - М.: Академия Естествознания, 2003, 10. С. 12.
2. Верещагин И.А. Постэфирная гиперсимметрия Вселенной. Часть 2 // Успехи современного естествознания. - М.: Академия Естествознания, 2003, 11. С. 13.
3. Генкин И.Л., Чечин Л.М. // Известия вузов. Физика. - Изд. ТГУ, 1995, 6. С. 103.
4. Малюта А.Н. Закономерности системного развития. - Киев: Наукова думка, 1990. СС. 48 - 52.
5. Маркин Маркин В.С. и др. Физика нервного импульса // Успехи физических наук, 1977, 10.
6. Шкловский И.С. Космическое радиоизлучение. - М.: ГИТТЛ, 1956.

Библиографическая ссылка