Рассмотрим уравнение
![]() (1)
(1)
где а- действительная постоянная, причем ![]() в характеристическом треугольнике D, ограниченном характеристиками
в характеристическом треугольнике D, ограниченном характеристиками ![]() уравнения (1) и отрезком
уравнения (1) и отрезком ![]() прямой y=0.
прямой y=0.
Задача. Найти регулярное в области D решение u(x,y) уравнения (1) из класса ![]() , удовлетворяющее краевым условиям
, удовлетворяющее краевым условиям
![]() , (2)
, (2)
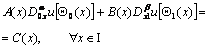 (3)
(3)
где ![]() - заданные непрерывные функции, причем
- заданные непрерывные функции, причем
![]() - аффиксы точек пересечения характеристик уравнения (1), выходящих из точки
- аффиксы точек пересечения характеристик уравнения (1), выходящих из точки ![]() с характеристиками АС, ВС соответственно;
с характеристиками АС, ВС соответственно; ![]() - соnst,
- соnst,
![]() -операторы дробного в смысле Римана-Лиувилля интегро-дифференцирования, определяемые по формулам [1]
-операторы дробного в смысле Римана-Лиувилля интегро-дифференцирования, определяемые по формулам [1]
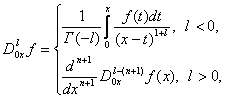
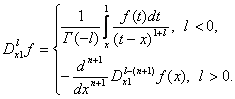
В зависимости от интервалов изменения порядка дробной производной в краевом условии, при определенных ограничениях гладкости на известные функции доказано, что задача либо редуцируется к уравнению Вольтерра второго рода, которое однозначно и безусловно разрешимо, либо сводится к интегро-дифференциальному уравнению, которое имеет более одного решения.
СПИСОК ЛИТЕРАТУРЫ
- Hardy G., Littwood S.-Math. Zs, 27, 1928.
Библиографическая ссылка
Лайпанова А.М. НЕЛОКАЛЬНАЯ КРАЕВАЯ ЗАДАЧА ДЛЯ ВЫРОЖДАЮЩЕГОСЯ ГИПЕРБОЛИЧЕСКОГО УРАВНЕНИЯ // Успехи современного естествознания. 2004. № 8. С. 122-123;URL: https://natural-sciences.ru/ru/article/view?id=13330 (дата обращения: 31.12.2025).



