Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы

Иванов Е. М.

Показано, что бытующее до сих пор утверждение, что центростремительные и гироскопические силы работы не совершают, неверно. При движении тела с постоянной скоростью по круговой орбите непрерывно затрачивается работа на изменение направления движения (поворот вектора скорости).

Статья в формате PDF

187 KB

В школьных [1] и вузовских [2-4] курсах физики для вычисления работы A обычно используют формулу

                          (1)

где - проекция силы F на направление перемещения dS, α- угол между векторами F и dS.

Формально применяя (1) для любой центростремительной силы, вызывающей движение тела по окружности (например, для силы Лоренца при вращательном движении заряда q в магнитном поле, или для силы тяготения при движении спутника вокруг Земли по круговой орбите) утверждают, что центростремительные силы работы не совершают, так как они всегда перпендикулярны вектору скорости, а .

Это утверждение довольно странное, ведь, например, движение спутника - это бесконечное падение тела под действием силы тяжести. Движение спутника аналогично движению тела, брошенного с башни высотой h в горизонтальном направлении с начальной скоростью . При падении тела на Землю сила тяжести совершает работу . Движение спутника отличается только численными параметрами: необходимо сообщить телу первую космическую скорость , где R₃ - радиус Земли, и для уменьшения аэродинамического сопротивления увеличить высоту h до 300÷ 400 км. Скорость  - не результат действия силы тяготения, она получена, как и подъем на высоту h, в результате работы двигателей ракеты. Сила тяготения вызывает падение спутника (криволинейное движение с постоянной скоростью), при этом совершается работа, затрачиваемая на изменение направления движения тела.

Классическая механика начинается с закона инерции Галилея (I закон Ньютона), из которого следует [2]: всякое тело оказывает сопротивление при попытках привести его в движение или изменить модуль или направление его скорости. Это свойство тел называется инертностью. Чтобы преодолеть сопротивление, необходимо приложить усилие, т.е. совершить работу!

Для разгона неподвижного свободного тела до скорости  необходимо в направлении предполагаемого перемещения приложить, например, в течение времени  постоянную силу F₀, т.е. подействовать на тело импульсом силы , в результате этого воздействия тело массы m приобретет импульс (количество движения), равный :

                   (2)

Если сила распределена по произвольному закону F(t), то

или можно ввести среднее значение силы

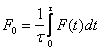
Работа, затраченная на разгон свободного, первоначально неподвижного тела со скоростью , можно представить в следующем виде:

                    (3)

где S-отрезок перемещения, на котором действовала сила F₀. Для математического и физического упрощения можно ввести понятие мгновенной силы, для чего следует устремить интервал действия силы , а величину силы . Тогда получим мгновенную силу в виде , где - -функция Дирака [5]. Величину I₀ будем называть единичным импульсом силы.

Свободное тело, получившее импульс , в дальнейшем будет двигаться прямолинейно и равномерно («Вечное движение»-perpetuum mobile).

Определим теперь работу, которую надо затратить, чтобы изменить направление движения тела, т.е. повернуть вектор скорости  на некоторый угол α. При изменении направления движения ( ) кинетическая энергия тела не изменяется, но работа должна быть затрачена, так, как, тело оказывает сопротивление к попытке изменить направление его скорости. Изменение направления движения будем производить за счет действия мгновенной силы , т.е. за счет передачи единичного импульса силы I₂. В векторной форме (рис.1) это запишется так:

           (4)

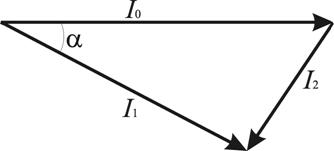
Рисунок 1.

где модуль . По теореме косинусов находим:

                                 (5)

Тогда аналогично (3) работу поворота тела массы m при постоянной скорости  на угол α от первоначального направления движения можно записать в виде:

;       (6)

Для углов поворота, больших чем , например , учитывая периодичность функции cosα, надо к работе поворота на угол 180^о ( ) добавить работу . Обозначим

- кинетическая энергия тела. В таблице I приведена работа поворота  в зависимости от угла поворота α.

Таблица 1.

Таким образом, при повороте тела, движущегося под действием центростремительной силы по окружности, на 360^о, т.е. на один оборот затрачивается работа, равная 8K₀, (восемь кинетических энергий тела). При движении спутника эту работу совершает гравитационная сила. При движении заряда q в магнитном поле эту работу совершает сила Лоренца. А при механическом движении - сила упругости нити или опоры.

Приведем еще один пример движения заряда по окружности в электрическом поле (рис.2).

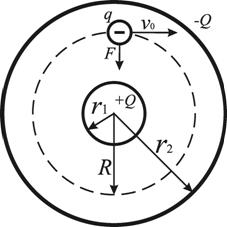
Рисунок 2.

Заряд q со скоростью  влетает по касательной в цилиндрический или сферический конденсатор. На заряд действует электрическая сила Кулона F=qE, которая становится центростремительной силой.

                         (7)

где E - напряженность электрического поля конденсатора, R - радиус орбиты движения заряда. Для цилиндрического конденсатора:

                     (8)

где Q - заряд конденсатора, h - его длина,  - электрическая константа. Для сферического конденсатора:

                        (9)

Движение заряда в сферическом конденсаторе может служить моделью классической теории атома водорода Резерфорда. Она эквивалентна движению спутника под действием силы всемирного тяготения:

                  (10)

где G - гравитационная постоянная, M - масса Земли.

Проверим достоверность формулы (6), для чего проведем ее вывод другим путем. Будем использовать принцип суперпозиции механических движений, т.е. рассматривать круговое движение тела как результат независимых друг от друга движений вдоль координатных осей X и Y (рис.3).

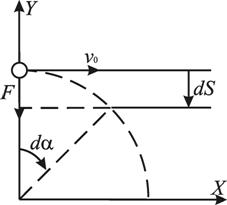
Рисунок 3.

Пусть тело массы движется со скоростью  по круговой орбите радиуса R под действием центростремительной силы . При повороте на бесконечно малый угол dα тело проходит путь dS в направлении оси Y. Работа, совершаемая силой F в направлении перемещении dS в соответствии с (1) будет равна , так как направления векторов F и dS совпадает. Поскольку , то дифференциал перемещения:

и элементарная работа будет равна:

                             (11)

Работа, совершаемая силой F при повороте на конечный угол α, найдется интегрированием по углу поворота

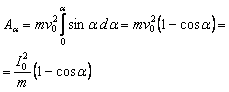              (12)

т.е. получили формулу (6). Так как , то (12) можно переписать в виде:

                   (13)

Рассмотрим случай поворота на угол  (рис.4).

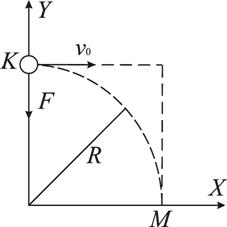
Рисунок 4.

В соответствии с (13)  есть вертикальное перемещение S, равное отрезку LM=R, т.е. . В соответствии с принципом суперпозиции (или независимости движений) перемещение по дуге KM можно рассматривать как результат движения по прямой KL, совершаемое по инерции, без совершения работы, и движение по вертикали LM=KO под действием силы F, которая совершает работу .

Так в чем же причина более столетнего заблуждения в физике по поводу работы, совершаемой центростремительными силами? А причина очень проста (рис.5).

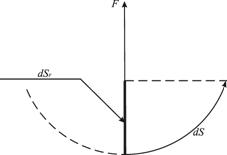
Рисунок 5.

Скалярное произведение векторов F и dS надо записывать двояко. Выражение (1) надо дополнить:

                   (14)

где F_S - есть проекция действующей силы F на направлении перемещения dS, а dS_F есть, наоборот, проекция перемещения dS на направления действия силы F. При криволинейном движении, когда вектор силы F перпендикулярен dS, надо использовать выражение , поскольку проекция F_S равна нулю.

В заключении сформулируем следующий принцип:

Если потенциальная (консервативная) сила является центростремительной, то на перемещение тела массы m (заряда q) по замкнутому кольцевому пути, проходящего по линии постоянного потенциала (электрического, гравитационного или упругого) затрачивается работа, равная , где  - скорость его равномерного движения по окружности.

То же самое относится и к гироскопической силе Лоренца при движении заряда в магнитном поле.

СПИСОК ЛИТЕРАТУРЫ

1. Кикоин И. К., Кикоин А. К. Физика: Учеб. для 9 кл. средн. шк. - М.: Просвещение, 1990.
2. Сивухин Д. В. Общий курс физики. Том I. Механика. - М.: Наука, 1989.
3. Детлаф А. А., Яворский Б. М. Курс физики: Учебн. пособие для вузов. - М.: Высш. шк., 1989.
4. Матвеев А. Н. Механика и теория относительности: Учебн. пособие для физ. спец. вузов.-М.: Высш. шк., 1986.
5. Арсенин В. Я. Математическая физика. - М.: Наука, 1966.

Библиографическая ссылка