Вещество угля на молекулярном уровне состоит из двух взаимосвязанных частей:
- ядер (кристаллитов), обладающих структурой графита;
- боковой бахромы, состоящей из кислородосодержащих групп, играющих роль перемычек и связывающих первичные элементы между собой, а кристаллиты придают жесткость и укрепляют всю систему.
Несовершенная упаковка кристаллитов и образованных ими молекулярных слоев приводит к микропористости. Классификация пор зависит от возможного фазового состояния поглощенного в порах газа и включает в себя пять групп:
- микропоры;
- субмикропоры;
- мезопоры;
- макропоры;
- супермакропоры.
Находясь в микропорах, молекулы сорбата взаимодействуют между собой, и при их плотной упаковке в микропорах это молекулярное взаимодействие является взаимодействием отталкивания. При изменении силового состояния структурных элементов угольного вещества часть энергии молекулярного отталкивания молекул сорбата может передаваться угольному скелету, а при его разгрузке от внешних сил вызвать дополнительное растяжение и, тем самым, обеспечить локальное разрушение угольного вещества. Как показали исследования [1], энергия межмолекулярного отталкивания молекул сорбата, аккумулированная в микропорах, соизмерима с энергией разрыва вандерваальсовских и водородных связей между структурными элементами. При этом, взаимодействие отталкивания молекул сорбата и угольного вещества может не только усилить эффект разрушения угля, но и является начальной движущей силой этого процесса, обладая определенной упругостью.
Сорбированный в микропорах газ влияет не только на характеристики разрушения угля, но и на формирование в нем новых микропористых сорбционных структур. Эта закономерность прослеживается и для влажных углей. Хотя наличие влаги не изменяет количество самих микропористых структур по сравнению с сухими углями, однако, она снижает величину энергетического барьера формирования новой микропористой структуры.
Рассмотрим энергетический баланс микропористых сорбционных структур. Выделим элемент горной среды массива ωijk∈Ω. Будем считать, что в пространстве Ω(x1,x2,x3) горного массива до начала горных работ t<t0, все элементы ωijk упорядочены и образуют пространственную решетку (каркас) среды. При деформации массива (t>t0) элемент ωijk поглощает энергию упругой деформации ΔEijk, которая увеличивает внутреннюю энергию элемента ΔUijk. Разность (ΔEijk - ΔUijk) характеризует переход элемента среды ωijk с одного энергетического состояния в другое, отдавая избыток энергии в виде звуковой волны. Элементы ωijk, находящиеся в возбужденном состоянии, могут либо поглощать энергию, переходя на более высокий уровень либо, разрушаясь и отдавая энергию, возвращаться на более низкий энергетический уровень, т.е. имеет место бифуркация. Энергетический баланс обоих видов поглощения равен [2]
![]() . (1)
. (1)
Учитывая определение интенсивности ![]() , где с - скорость звука в данной среде, найдем коэффициент поглощения энергии K:
, где с - скорость звука в данной среде, найдем коэффициент поглощения энергии K:
 . (2)
. (2)
Если ![]() , то коэффициент поглощения K>0, а это означает затухание звуковой волны. При
, то коэффициент поглощения K>0, а это означает затухание звуковой волны. При ![]() K<0 и тогда интенсивность звукового поля растет, что означает образование ударной волны разрушения. Таким образом, сорбционные процессы инициируют упругие волновые поля в угольном массиве.
K<0 и тогда интенсивность звукового поля растет, что означает образование ударной волны разрушения. Таким образом, сорбционные процессы инициируют упругие волновые поля в угольном массиве.
Упругие волны, интерферируя с преломленными ударными волнами, образуют интерференционные волны (ИВ). Последние затухают значительно быстрее, чем волны более низкого диапазона, так как коэффициент K пропорционален квадрату частоты. В то же время ИВ обладают высокой интенсивностью при относительно небольших амплитудах колебания. Затухающие ИВ превращаются в слабые ультразвуковые волны. Наличие влаги в порах угольного пласта при наличии ультразвуковых полей вызывает явление кавитации. Кавитационные микроскопические пузырьки, попадая в область разряжения, сильно расширяются за счет того, что давление содержащегося внутри газа превосходит суммарное действие поверхностного натяжения и давления жидкости.
Изменение радиуса кавитационной полости в поле ультразвуковой волны хорошо описывается уравнением Нолтинга-Непайреса [3], однако это уравнение допускает только численное решение.
Для нахождения кинематических характеристик захлопывающегося кавитационного пузырька рассмотрим наиболее простую задачу о смыкании стенок сферической полости в несжимаемой жидкости под действием постоянного давления газа [2]. Кинетическая энергия массы смыкающейся жидкости равна
![]() . (3)
. (3)
С учетом уравнения неразрывности
![]() , (4)
, (4)
получим
![]() . (5)
. (5)
Эта кинетическая энергия равна работе, совершенной силой давления P, по уменьшению объема полости от первоначального значения ![]() до конечного
до конечного ![]() ,т.е.
,т.е.
![]() . (6)
. (6)
Приравнивая формулы (5) и (6), получаем выражения для скорости движения стенок захлопывающейся полости
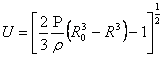 . (7)
. (7)
Из выражения (7) найдем полное время ∂t захлопывания пустой полости с начальным радиусом R0. Учитывая, что ![]() , и вводя замену переменных
, и вводя замену переменных ![]() , найдем
, найдем
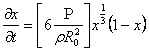 , (8)
, (8)
откуда
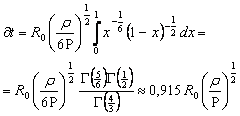 . (9)
. (9)
Расчеты по формуле (9) показывают, что время захлопывания пустой полости изменяется от ![]() .
.
Исследуем изменение давление внутри захлопывающегося пузырька. Давление в полости пузырька подчиняется политропическому закону
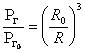 . (10)
. (10)
Благодаря наличию в кавитационном пузырьке газа, скорость движения газа не будет стремиться к бесконечности, а радиус полости не сократится до нуля, как это вытекает из формулы (7) . Найдем минимальный радиус пузырька исходя из работы по сжатию газовой смеси:
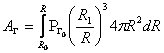 . (11)
. (11)
при γ = 1,31 интеграл (11) принимает вид
 , (12)
, (12)
где минус обусловлен направлением действующих сил.
При полном сжатии полости до минимального радиуса вся энергия смыкающейся жидкости, определяемая формулой (6), идет на работу сжатия парогазовой смеси (12), а значит ( при ![]() ),
),
![]() . (13)
. (13)
Отношение ![]() (его принято называть параметром газосодержания) составляет
(его принято называть параметром газосодержания) составляет ![]() [3]. Следовательно, радиус пузырька при его захлопывании уменьшается в десятки раз. В момент захлопывания пузырька развивается давление до
[3]. Следовательно, радиус пузырька при его захлопывании уменьшается в десятки раз. В момент захлопывания пузырька развивается давление до ![]() МПа, порождающее сферические, быстро затухающие в пространстве ударные волны. Таким образом, происходит диспергирование угля до мелких фракций типа угольной муки. Наличие мелкодиспергированных участков в угольных пластах характерно для зон, опасных по внезапным выбросам угля и газа.
МПа, порождающее сферические, быстро затухающие в пространстве ударные волны. Таким образом, происходит диспергирование угля до мелких фракций типа угольной муки. Наличие мелкодиспергированных участков в угольных пластах характерно для зон, опасных по внезапным выбросам угля и газа.
СПИСОК ЛИТЕРАТУРЫ
- Айруни А.Т. Бобин В.А. Модель макроструктуры угольного вещества. //Изв. ВУЗов, Горный журнал, №2,1987, с 1-7.
- Беспятов Г.А., Вылегжанин В.Н., Золотых С.С. Синергетика выбросоопасной горной среды. Новосибирск. Наука. Сибирская издательская фирма РАН.1996 г., с 190.
- Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. -М.: Наука, 1966 г.
Работа представлена на V научную конференцию «Успехи современного естествознания», 27-29 сентября 2004 г., РФ ОК «Дагомыс», г. Сочи
Библиографическая ссылка
Беспятов Г.А. ТЕРМОГАЗОДИНАМИЧЕСКАЯ МОДЕЛЬ РАЗРУШЕНИЯ УГОЛЬНЫХ ПЛАСТОВ // Успехи современного естествознания. 2004. № 10. С. 103-104;URL: https://natural-sciences.ru/ru/article/view?id=13630 (дата обращения: 07.03.2026).



