Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы

Семенчин Е.А.

Предложена нестационарная математическая модель рассеяния примеси в трехслойной атмосфере (приземный, пограничный слои, слой свободной атмосферы). Приведены результаты исследования этой модели аналитическими методами в случае рассеяния легкой, сохраняющейся примеси при постоянной скорости ветра.

Статья в формате PDF

130 KB

Процесс рассеяния примеси в турбулентной атмосфере описывается начально-граничной задачей [1-3]

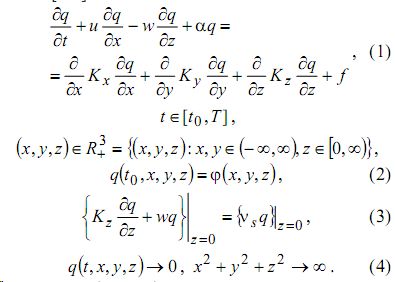
Здесь q =q (t, x, y, z) - функция, значения которой в каждый момент времени t € [t₀ , T ] в точках (x,y,z) € R³₊ совпадают со значениями осреднен
ной  концентрации  примеси,  u - скорость перемещения примеси (скорость ветра), направление которой  совпадает  с  направлением  оси 0х,  w -скорость вертикального осаждения примеси, α - коэффициент,  характеризующий  изменения  ее концентрации засчет различных превращений K_x ,  K_y ,  K_z  -коэффициенты турбулентного обмена  соответственно вдоль осей 0х, 0y, 0z, f=f(x,y,z)-  функция,  описывающая количество примеси, вырабатываемой  в  атмосфере источником в момент t € [t₀,T].
Задачу  (1)-(4) следует рассматривать с уравнением неразрывности [1]:

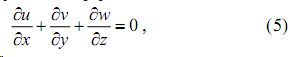
где u , v , w - компоненты вектора скорости перемещения примеси соответственно вдоль осей 0х, 0y, 0z.

Обычно  полагают  [1-3],  что  u=u(z), K_x= K_x (z), Ky = K_y (z), K_z = K_z (z)  являются непрерывно  дифференцируемыми  функциями аргумента z, z € [0, ∞), K_x= K_y (z), w=const, α= α(t) -  непрерывная  функция ,  Q   - мощность источника,  R (t,x,y,z) - функция, которая  выражается  через  δ -функцию  Дирака, φ (x,y,z)  - непрерывная функция аргументов  x , .  Если имеют место&данные ограничения и декартова система  координат  сориентирована таким образом, чтонаправление ветра совпадает с направлением оси 0х, то  соотношение (5) выполняется тождественно. Поэтому в дальнейшем  оно  учитываться не будет. 

Задача  (1)-(4) представляет собой математическую модель рассеяния примеси в пространстве 
Такая  модель неплохо описывает изменения концентрации примеси в атмосфере. Однако она не  учитывает  многослойность атмосферы.  На самом деле в  атмосфере принято выделять два слоя: тропосферу (до  высоты11 км от уровня моря)  и  стратосферу (простирающуюся  по высоте от 11 до 40 км).  В  свою очередь в тропосфере выделяют три слоя: приземный, пограничный и верхний (слой свободной  атмосферы) [4,5]. Рассеяние  примеси в  верхнем слое  атмосферы и стратосфере проистекает примерно одинаково (по одним и  тем  же законам). Однако процесс рассеяния примеси в каждом из трех указанных слоев тропосферы имеет свои особенности [2], которые целесообразно  учитывать  в модели (1)-(4).
Стационарные математические модели  диффузии примеси в многослойной атмосфере были впервые предложены и изучены численными методами  в  [6-9].  В  данной работе эти модели обобщаются  на  нестационарный  режим  диффузии и изучаются аналитическими методами. 
Разобьем  пространство R³₊   на  три  подпространства: 

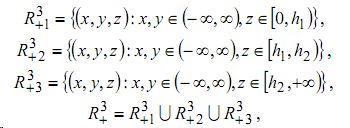
где h₁ - высота приземного слоя атмосферы, h₂ - высота пограничного слоя. h₁,h₂ могут быть вычислены по формулам, приведенным в  [2].
Предлагается нестационарная математическая модель рассеяния примеси в трехслойной атмосфере, представляющая собой совокупность трех задач:

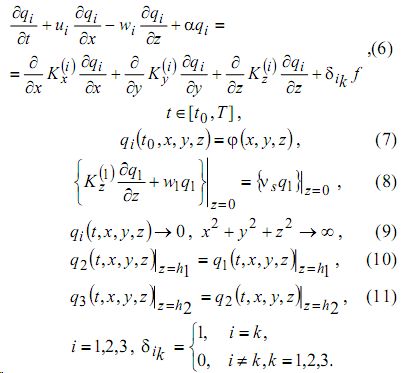
> Предполагается, что задачи (6)-(11) рассматриваются последовательно: вначале при i =1 , затем  при i =2 , при i = 3 .Проведем исследование модели (6)-(11) аналитическими методами в случае:

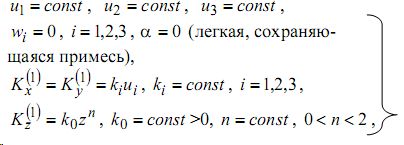
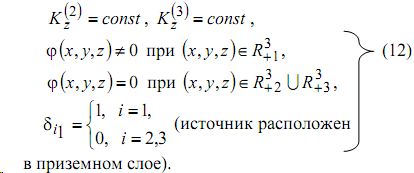
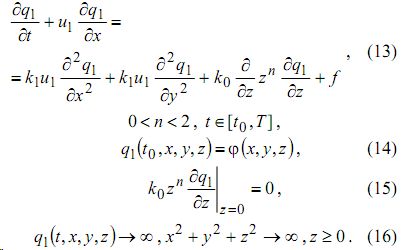
Решение  задачи  (13)-(16)  приведено  в  [3].  Оно имеет вид:

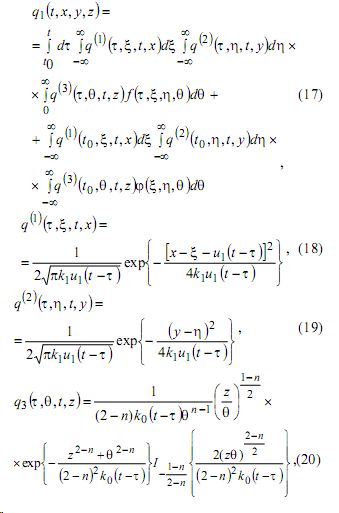
I _-β (α) - функция Бесселя мнимого аргумента

При i =2 имеем задачу:

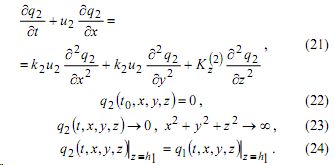
Преобразуем данную задачу, положив

  (25)

Учитывая (24), (25), будем иметь:

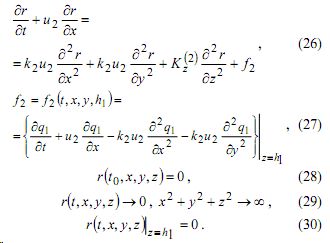
Непосредственным подсчетом можно убедиться, что решение задачи (26)-(30) имеет вид [3]:

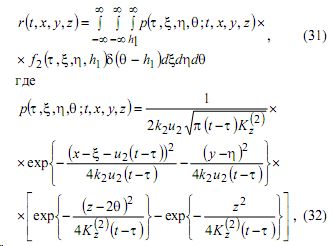
Учитывая (25) и воспользовавшись свойствами δ-функции, найдем решение задачи (21)-(24):

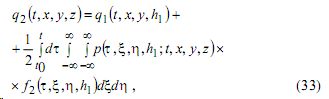
p , f 2 заданы соответственно выражениями (32), (27)

При i =3 имеем задачу:

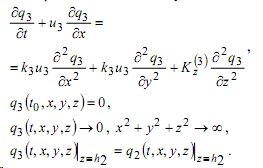
Решение этой задачи строится точно так же, как и решение задачи (21)-(24) и имеет вид:

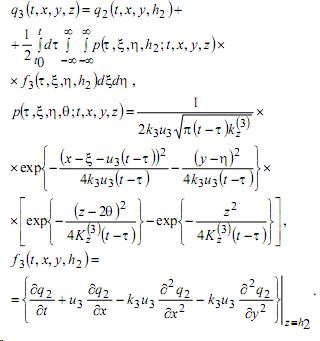
Литература

1. Марчук  Г.И. Математическое  моделирование в проблеме окружающей среды. - М.: Наука, 1982.-320 с.
2. Берлянд М.Е. Современные проблемы атмосферной  диффузии  и  загрязнения  атмосферы. - Л.:Гидрометеоиздат, 1975.-448 с.
3. Семенчин  Е.А.  Аналитические решения краевых задач в математической модели  атмосферной диффузии. -Ставрополь: изд-во СКИ-УУ, 1993.-142с.
4.  Матвеев Л.Г. Курс общей метеорологии. Физика атмосферы. - Л.: Гидромеоиздат, 1984. -752 с.
5. Рихтер Л.А. Тепловые электростанции и защита атмосферы. - М.: Энергия, 1975.-312 с.
6. Бабешко В.А., Гладской И.Б., Зарецкая М.В., Кособуцкая Е.В. Исследование распространения загрязняющих веществ от точечного источника  в  стратифицированной  атмосфере/ Тез. докл. 2-й международной конф. «Современные проблемы механики сплошной среды». Ростов-на-Дону, 19-20 сент. 1996. С. 10-13.
7. Бабешко В.А., Зарецкая М.В., Кособуцкая Е.В. Об одной модели распространения загрязняющих веществ по глубине водного потока// Доклады РАН. 1994. Т.337. №5 С. 660-661.
8. Бабешко В.А., Гладской И.Б., Зарецкая М.В., Кособуцкая Е.В. К проблеме оценки выбросов загрязняющих веществ источниками различных типов// Доклады РАН. 1995. Т.342. №6 С. 835-838.
9. Кособуцкая Е.В. Некоторые модели распространения опасных загрязняющих веществ в стационарных условиях. Дис. на соиск. ученой степени канд. физ.-мат. наук. - Краснодар, 1998.- 124 с.

Библиографическая ссылка