Распределение теплового поля в сечении описывается двумерным уравнением стационарной теплопроводности в неоднородной среде в прямоугольной области
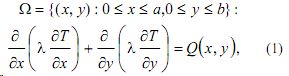
где T( x, y) - температура, λ( x, y) - коэффициент удельной теплопроводности, Q -мощность внутренних источников и стоков тепла (теплогенерация пород). Для задания граничных условий используется средняя температура по верхности Земли T0 и тепловой поток qm ( x) на границе литосферы и астеносферы (зоны частичного плавления пород).
Для определения функции T( x, y) распределения λ( x, y) и Q( x, y) должны быть известными. Для получения этих распределений используются опубликованные данные для разных типов пород региона, а также геологическая интерпретация сейсмических исследований.
Уравнение (1) преобразуем, получив линейное дифференциальное уравнение второго порядка эллиптического типа. Итак, задача решается конечно-разностным методом. Для этого строится сетка с постоянным или переменным шагом.
В работе для итерационных расчетов используются метод Гаусса-Зейделя и метод релаксаций. При чем Метод Гаусса-Зейделя применительно к эллиптическим разностным уравнениям называется методом Либмана или методом последовательных смещений.
Таким образом, в данной работе с помощью численного эксперимента и сравнения с точным решением удалось установить, что предложенная разностная схема при разрывной функции λ(x,y) обладает первым порядком точности. Применение обобщенного правила Рунге для оценки погрешности численного решения показало хорошее соответствие полученных оценок фактическим погрешностям. Применение повторной экстраполяции позволило на несколько порядков уточнить полученные численные данные.
Таблица 1. Сравнение численного результата с аналитическим
|
y |
T ( yi ) |
T ( y) |
ε, % |
|
0 |
5 |
5 |
- |
|
1000 |
19.55 |
19.39 |
0.8 |
|
2000 |
33.93 |
33.77 |
0.5 |
|
3000 |
48.30 |
48.13 |
0.3 |
|
4000 |
62.63 |
62.45 |
0.3 |
Программный продукт реализован в среде Microsoft Visual C++ версии 5.0 (под Windows), и зарегистрирован в РОСПАТЕНТЕ. Кроме того получены справки о практическом и научном использовании данной работы.
Библиографическая ссылка
Гаврилов В.В. Численно-аналитическая модель теплового поля поверхностных слоев земли // Успехи современного естествознания. 2003. № 6. С. 113-114;URL: https://natural-sciences.ru/ru/article/view?id=14514 (дата обращения: 15.01.2026).



