В данной работе авторы предприняли взглянуть на эту задачу с точки зрения экономической динамики.
Следует отметить, что динамические дифференциальные модели уже давно и успешно используются для математического моделирования самых разнообразных по своей природе процессов. Достаточно упомянуть широко использующуюся в экологии модель «хищник-жертва» Вольтера [2], математическую теорию развития эпидемий, модели боевых действий.В качестве классических примеров дифференциальных моделей экономической динамики отметим модель Эванса установления равновесной цены на рынке одного товара, односекторную модель экономического роста Солоу [4], однопродуктовые динамические макроэкономические модели Леонтьева [3].
Задача решалась в следующей постановке.
На рынке однородного товара присутствуют две основные фирмы, разделяющие его между собой, т.е. имеет место классическая дуополия.
Безусловно, это является весьма сильным предположением, однако оно вполне оправдано в тех случаях, когда доля продаж остальных конкурентов на рассматриваемом сегменте рынке пренебрежимо мала. Хорошим примером может служить отечественный рынок микропроцессоров, который по существу разделили между собой две фирмы: Intel и AMD.
Изменение объемов продаж конкурирующих фирм с течением времени описывается следующей системой дифференциальных уравнений:
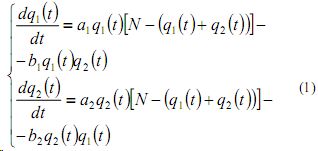
с начальными условиями
q1(0)=q01, q2(0)=q02 (2)
Здесь и далее использованы следующие обозначения:
q1(t) - объем продаж фирмы I;q2(t)-объем продаж фирмы II
N - объем рассматриваемого сегмента рынка сбыта;
a1 , b1 , a2 , b2 -положительные коэффициенты, характеризующие степень влияния различных факторов на изменения объема продаж первой и второй фирмы соответственно.
Уравнения (1) получены из следующих самых общих соображений.
С достаточным основанием можно утверждать, что скорость изменения объемов продаж фирм со временем задается формулами:
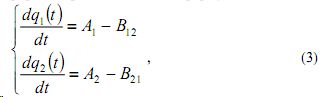
где Ai и Bij являются в общем случае функциями qi.
Задача теперь состоит в определении вида зависимостей Ai=Ai (q) и Bij =Bij (q).
Функция Ai (q) описывает влияние внутренней среды предприятия на рост объема продаж и может быть с учетом логистической поправки записана в виде [2]:
![]()
Заметим, что здесь учтен тот факт, что суммарный объем продаж двух фирм qi+qj не может превышать N.
Слагаемое Bij (q) выражает влияние внешней среды предприятия на рост объема продаж и учитывает уменьшение объема продаж i-ой фирмы за счет роста продаж j-ой: bi qi q j .
В результате подобных рассуждений удается построить систему дифференциальных уравнений (1)-(2), которая тривиально обобщается на случай произвольного количества конкурирующих предприятий.
Для удобства дальнейшего исследования введем в рассмотрение безразмерные переменные:
τ= a1(Nt) - безразмерное время, (5)
yi =qi /N - безразмерный объем продаж i-ой фирмы (i=1,2).
После этого модель задачи приобретает вид
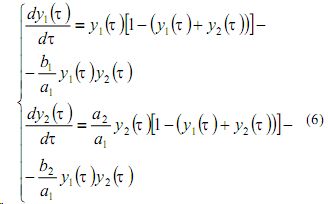
Начальные условия приобретают вид:y1(0)=y01, y2(0)=y02
Таким образом, мы приходим к задаче Коши для системы обыкновенных дифференциальных уравнений (6)-(7), представляющей собой основу для математического моделирования рассматриваемого процесса.
Система (6)-(7) интегрировалась ПЭВМ для широкого диапазона параметров и начальных условий с использованием стандартного алгоритма Рунге-Кутта четвертого порядка [5], реализованного в среде разработки VBA для пакета MS Office 2002 XP.
Некоторые полученные результаты приведены ниже в виде графиков зависимости безразмерных объемов продаж фирм y1 и y2 от безразмерного времени τ на рис. 1-3. На всех графиках по горизонтальной оси отложена величина τ, а по вертикальной оси- y1 и y2.
Рис.1. соответствует ситуации, когда на рынке присутствует только фирма I, т.е. имеет место классическая монополия. Система (1) в этом случае вырождается в задачу Коши для одного уравнения
![]()
или в безразмерном виде
![]()
Задача (9) допускает аналитическое решение в виде
![]()
причем ![]() что полностью согласуется с тем очевидным фактом, что рано или поздно фирма-монополист будет целиком контролировать рассматриваемый сегмент рынка сбыта.
что полностью согласуется с тем очевидным фактом, что рано или поздно фирма-монополист будет целиком контролировать рассматриваемый сегмент рынка сбыта.
Выражение (10) представляет собой уравнение хорошо известной логистической кривой [3], которая и представлена на рис. 1.
Рис. 2. иллюстрирует динамику процесса раздела рынка между двумя фирмами в том случае, когда их взаимным противодействием, учитываемым посредством коэффициентов b1 , b2 , можно пренебречь. Это соответствует ситуации, когда влиянием внешней среды предприятий на рост объемов продаж можно пренебречь по сравнению с влиянием внутренней среды. В этом случае единственным внешним фактором, ограничивающим увеличение объемов продаж, является изначальная ограниченность рынка сбыта.
Рис 3. соответствует наиболее общему случаю, когда в полной мере учитываются как внутренние, так и внешние факторы, определяющие развитие обоих предприятий.
Обращает на себя внимание тот факт, что при прочих равных условиях в конечном итоге в выигрыше оказывается фирма с бо´льшим значением коэффициента ai и с ме´ньшим значением коэффициента bi .
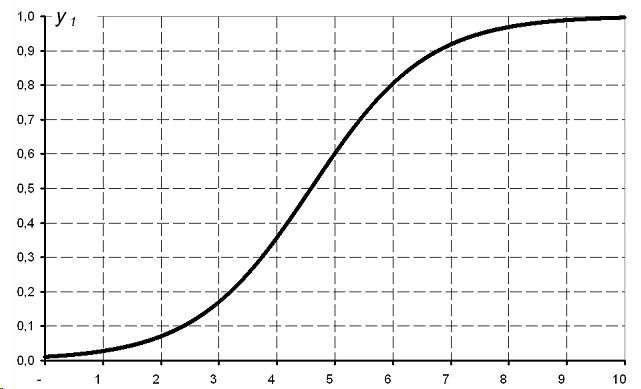
Рис. 1. Динамика изменения объемов продаж при a1=0,5; a2=b1=b2=0; ,y1(0) =0,01,y2(0)= 0,00.
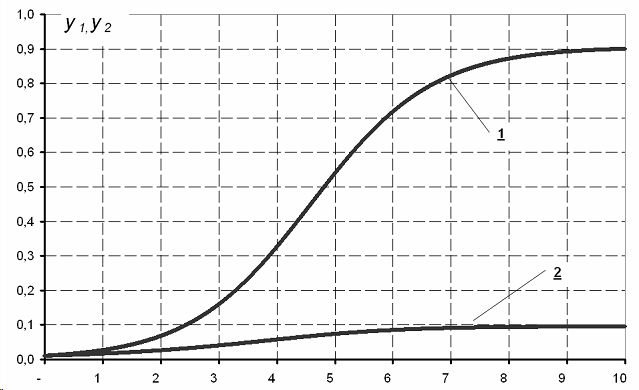
Рис. 2. Динамика изменения объемов продаж при a2/a1= 0,5; b1/a1=0,0; b2/a1=0,0 ,y1(0)= 0,01, y2(0)= 0,01 .
Следует также отметить, что зависимости отражает основные закономерности развития y1(τ) и y2(τ) имеют принципиально нелинейный характер, переживая «взлеты» и «падения», о чем особенно наглядно свидетельствует рис. 3.рассматриваемой ситуации, и использованные Анализ полученных результатов позволяет сделать вывод о том, что, несмотря на некоторую абстрактность, данная модель в целом адекватно для ее построения принципы могут быть с успехом применены для математического описания динамики развития различных экономических систем.
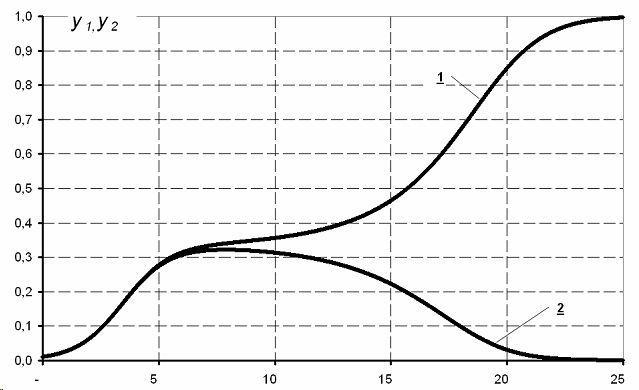
Рис. 3. Динамика изменения объемов продаж при a2/a1= 1,000; b1/a1=0,984; b2/a1=1,000 ,y1(0)= 0,01, y2(0)= 0,01 .
Литература
- Coleman C.S. Combat models // Differential equation models.-New York e.a., 1983.-P. 109131.
- Murray J. D. Some simple mathematical models in ecology// Math. Spectrum.-19831984.-V. 16, №2.-P. 48.-54.
- Бережной Л.И.. Теория оптимального управления экономическими системами: Учебное пособие.СПб.:ИВЭСЭП, Знание, 2002.-64 с.
- Малыхин В.И.. Математическое моделирование экономики. М., УРАО, 1998.-160 с.
- Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль.- Томск: МП «Раско», 1991.-272 с,: ил.
Библиографическая ссылка
Копылов А.В., Просвиров А.Э. ДИНАМИЧЕСКАЯ МОДЕЛЬ КОНКУРЕНЦИИ ДВУХ ФИРМ НА ОДНОРОДНОМ РЫНКЕ // Успехи современного естествознания. 2003. № 8. С. 29-32;URL: https://natural-sciences.ru/ru/article/view?id=14730 (дата обращения: 31.01.2026).



