Однолетние и многолетние травы. Они образуют травяной покров, мало влияющий на экологическую устойчивость территории из-за того, что они выращиваются искусственно на вспаханных полях. Поэтому площади таких трав относятся к пашне, как наиболее экологически агрессивной среде, создаваемой человеком вот уже почти 10 тысяч лет.
Исходные статистические ряды динамики урожайности сена однолетних и многолетних трав были приведены в предыдущей статье
Результаты идентификации покажем без приведения промежуточных результатов, так как процесс статистического моделирования биотехническим законом и его фрагментами и волновыми обобщениями ясен из предыдущего примера.
Однолетние травы. Рой всех точек статистического ряда с 1970 по 2004 гг. приведен на рисунке 1. Из-за пятилетней периодичности первой части исходных данных оставляем только отрезок календарного времени 1995‒2003 гг. с переносом начала координат на 1995 год при условии t = 0.
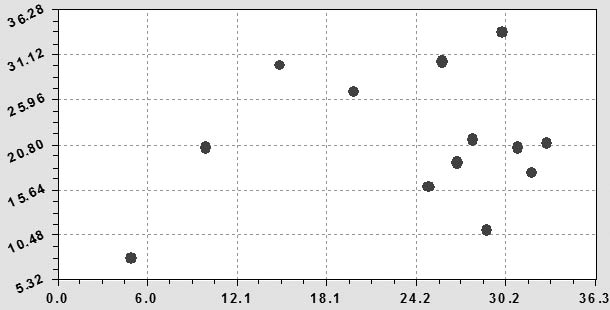
Рис. 1. Изменение урожайности сена однолетних трав РМЭ, ц/га
Картина распределения точек аналогична предыдущему примеру, когда редкие точки дополняются службой статистики ежегодными данными.
После идентификации была получена статистическая модель (рис. 2) вида
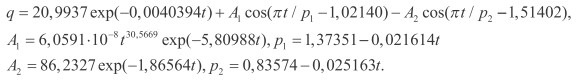 (1)
(1)
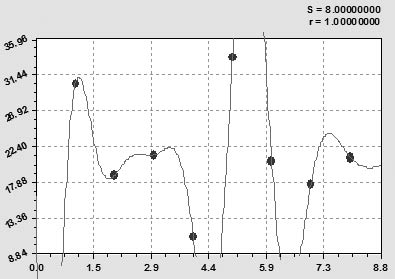
Рис. 2. Динамика урожайности сена однолетних трав РМЭ за период 1995‒2003 гг., ц/га
Уравнение (1) стало однозначной математической функцией с коэффициентом корреляции, равной единице. Если условно отбросить первые три точки, то с 1998 по 2003 годы наблюдается четкая вейвлет-функция, у которой относительно некого среднего значения урожайности около 20 ц/га площади графика сверху и снизу этого значения примерно равны.
Многолетние травы. За отрезок календарного времени 1995-2003 гг. получена модель (рис. 3), отличающаяся от предыдущей статистической закономерности, то есть
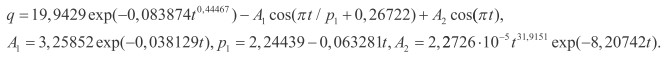 (2)
(2)
В этой закономерности p2 = 1, то есть появился цикл с двухлетней периодичностью изменения урожайности многолетних трав.
Амплитуда первого колебательного возмущения имеет закон гибели, а у второй волновой закономерности амплитуда изменяется по закону стрессового возбуждения, то есть по биотехническому закону.
При этом первая волновая зависимость является кризисной с убывающей амплитудой, но с увеличивающейся частотой колебания. Спад урожайности с такой кризисной волной, по-видимому, показывает влияние социально-экономического кризиса на поддержание высокой урожайности многолетних трав. Вторая волна с двухлетним периодом показывает позитивную адаптацию территории с многолетней травой к внешним воздействиям (однако это не имеет никакого отношения к так называемому адаптивному земледелию).
Сравнение естественных и улучшенных сенокосов. Из данных табл. 1 видно, что шкала времени изменилась, и условие t = 0 было принято для 1980 г. Из-за пятилетних псевдоциклов исключаем еще три точки, оставляя промежуток времени с 1995 по 2003 гг. После этого проводим повторную идентификацию по новым данным статистического ряда.
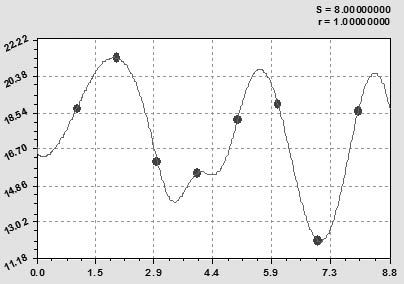
Рис. 3. Динамика урожайности сена многолетних трав РМЭ за 1995‒2003 гг., ц/га
Естественные сенокосы. После структурно-параметрической идентификации была получена статистическая закономерность (рис. 4) в виде формулы для описания динамики урожайности сена
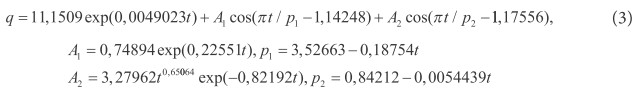
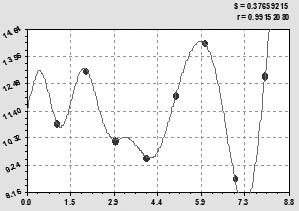
Рис. 4. Динамика урожайности сена естественных сенокосов РМЭ за 1995‒2003гг., ц/га
Первая составляющая модели (3) вполне обнадеживает, что с годами происходит экспоненциальный рост урожайности трав естественных лугов по первой составляющей. Вторая и третья составляющие, хотя и имеют колебательное изменение, однако являются положительно направленными. Они показывают хорошую адаптивную возможности луговых трав к изменяющимся внешним воздействиям, в том числе и антропогенным. Из-за антропогенного влияния в поведении травяного покрова по второй составляющей наблюдается рост амплитуды и частоты колебательного возмущения урожайности (возможен аварийный срыв нарастающего колебания). А по третьей составляющей при снижающейся в будущем амплитуде наблюдается также увеличение частоты колебательного возмущения (снижении половины периода колебания). Таким образом, анализ модели (3) дает возможность научного обоснования интенсивности травяного покрова на горизонт прогноза.
Улучшенные сенокосы. Улучшение интенсивности травяного покрова на улучшенных сенокосах выполняется человеком.
Закономерность (рис. 5) определяется уравнением
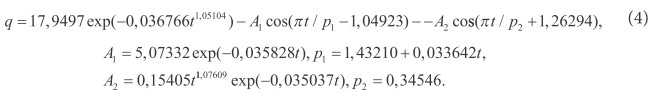
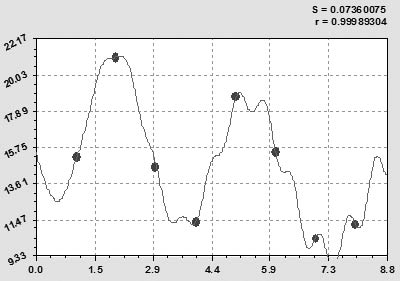
Рис. 5. Динамика урожайности сена улучшенных сенокосов РМЭ за 1995‒2003 гг., ц/га
Здесь оба волновых возмущения являются кризисными процессами. По сравнению с естественными сенокосами первая составляющая показывает спад урожайности, что объясняется кризисом в России.
Однако амплитуда обоих колебаний изменяется по закону стрессового возбуждения людей на социально-экономический кризис в стране, поэтому собственно к травяному покрову людские кризисы отношения не имеют.
А в модели (3) была позитивная адаптация самой луговой травы, так как человек вмешивается там только при проведении сенокосов. Сравнение показывает, что изучение динамики урожайности сена у естественных сенокосов в научном плане предпочтительнее, так как улучшенные сенокосы ведут себя капризно, как и полагается быт культурным растениям. Максимальная относительная погрешность модели (4) составляет 0,58 %. Обе модели (3) и (4) позволяют сформировать новый критерий эффективности улучшения сенокосов.
Эффект от улучшения сенокосов. Этот эффект по прибавке урожайности можно оценить несколькими способами:
а) вычитая значения показателей урожайности, улучшенных и естественных лугов друг от друга, можно определить абсолютную прибавку урожая сена, а поделив на урожайность естественных сенокосов - относительную прибавку;
б) поделив значения обоих показателей урожайности, друг на друга, можно определить коэффициент эффективности урожайности сена на улучшенных сенокосных лугах.
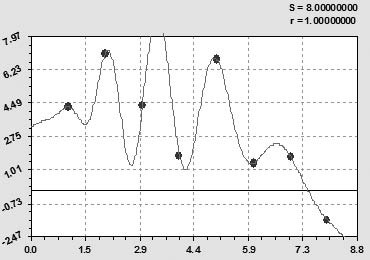
Рис. 6. Динамика прибавки урожая сена на улучшенных сенокосах РМЭ по сравнению с естественными сенокосами за 1995-2003 гг., ц/га
Прибавка урожая сена на улучшенных сенокосах по сравнению с естественными сенокосами (рис. 6) определяется уравнением
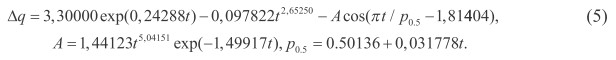
Остатки от формулы (5) очень малы (рис. 7) и поэтому коэффициент корреляции формулы (5) будет равен единице.
Однако видно, что даже малые остатки имеют свойство выявлять еще одну дополнительную волновую составляющую с периодом динамики прибавки урожая сена на улучшенных сенокосах в два года.
Коэффициент эффективности улучшения сенокосов в динамике за девять лет (рис. 8) определяется уравнением
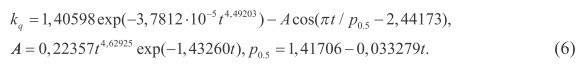
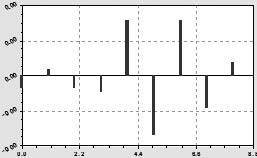
Рис. 7. Остатки готовой статистической модели тренда (13) прибавки урожайности сена на улучшенных сенокосах РМЭ по сравнению с естественными сенокосами за 1996‒2003 гг., ц/га
Характер закономерности изменился в волновой составляющей. Остатки приведены на рис. 9. Максимальная относительная погрешность в первой точке для 1995 г. равна 10,45 %. Однако этот год уже не влияет на прогноз значений показателя.
Если не учитывать первую точку, то максимальная относительная погрешность формулы (6) равна 0,95 %, поэтому доверие к этому уравнению для дальнейшего прогнозирования будет не ниже 99,05 %.
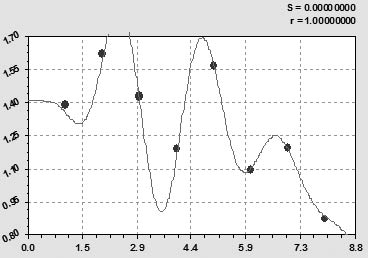
Рис. 8. Динамика коэффициента эффективности улучшения сенокосах РМЭ по отношению к урожайности естественных сенокосов за 1995‒2003 гг., ц/га
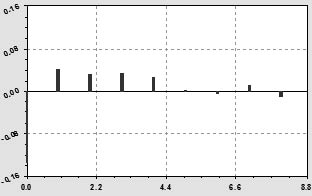
Рис. 9. Остатки готовой статистической модели тренда (14) коэффициента прибавки урожайности сена
на улучшенных сенокосах РМЭ по сравнению с естественными сенокосами
за 1996-2003 гг., ц/га
Прогнозирование урожайности сена. Основание прогноза равно девяти годам, поэтому при высоком доверии к математическим моделям можно выполнить прогнозирование на период прогноза также в девять лет. Для удобства принимается период по границам отрезка календарного времени, поэтому основание прогноза будет равно 2003‒1995 = 8 лет, а горизонт прогноза будет равен 2003 + 8 = 2011 год.
Для обоснования экологических, технологических и экономических мероприятий можно взять более жесткие условия прогноза, например одну треть основания прогноза. Однако принятие тех или иных горизонтов для обоснования проектных решений пока можно оставить за проектировщиком, а в научных обоснованиях пределом научного прогнозирования следует принять всю длину основания прогноза.
Урожайность сена естественных и улучшенных лугов при основании прогноза с 1996 по 2003 годы продолжает изменение до горизонта прогноза в 2010 г. по графикам всей функции отдельно по составляющим модели, приведенным на рисунке 10.
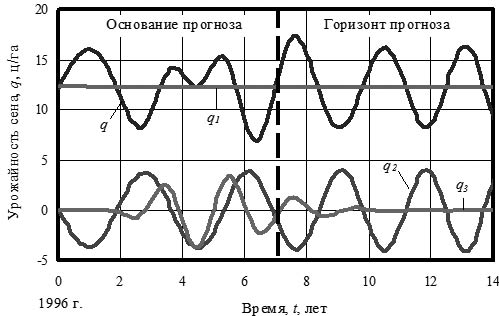
Рис. 10. Динамика урожайности сена на естественных и улучшенных сенокосах РМЭ
в период 1996‒2010 гг., ц/га
С 2006 г. третья составляющая приблизится к нулю, а затем она исключается из модели (8). Спад первой составляющей и кризисная вторая составляющая продолжатся надолго.
Однолетние травы изменяют свою урожайность так, как это показано на рисунке 11.
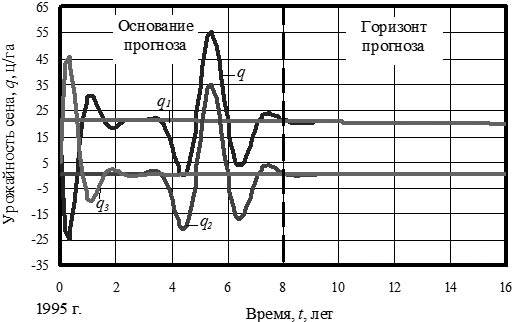
Рис. 11. Динамика урожайности сена из однолетних трав РМЭ в период 1995‒2011 гг., ц/га
Из графиков видно, культурные травы без ухода приблРис. 11. Динамика урожайности сена из однолетних трав РМЭ в период 1995‒2011 гг., ц/гаижаются к постоянному значению урожайности по сену.
Многолетние травы характеризуются графиками (рис. 12).
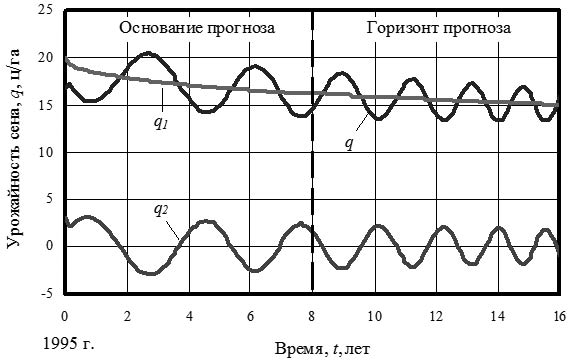
Рис. 12. Динамика урожайности сена из многолетних трав РМЭ в период 1995‒2011 гг., ц/га
Многолетние травы ведут себя весьма ритмично, сбавляя урожайность по первой составляющей и в дальнейшем. А третья составляющая практически незаметна.
Естественные сенокосы могут дать сена до 2011 г., как дано графиками на рис. 13.
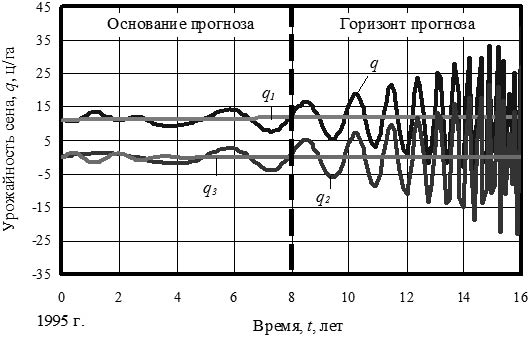
Рис. 13. Динамика урожайности сена на естественных сенокосах РМЭ в период 1995‒2011 гг., ц/га
Третья составляющая из-за малой амплитуды быстро вырождается. А вторая составляющая показывает адаптационные возможности луговой травы к росту урожайности, однако частота увеличивается и это может привести к тремору системы. Вместе с тем без участия человека естественные луга медленно по первой составляющей наращивают свою урожайность. Отсюда следует, что человеку просто не нужно мешать луговым экосистемам, росту и развитию травяного покрова.
Вторая волновая составляющая показывает возможность срыва динамической волны. Урожайность травы без участия человека может вырасти при активном поедании дикими травоядными животными. За почти 100 млн лет эволюции травяной покров Земли привык к животным.
Улучшенные сенокосы не только сбавляют без участия человека свою урожайность по сену, но еще имеют две кризисные колебательные возмущения (рис. 14).
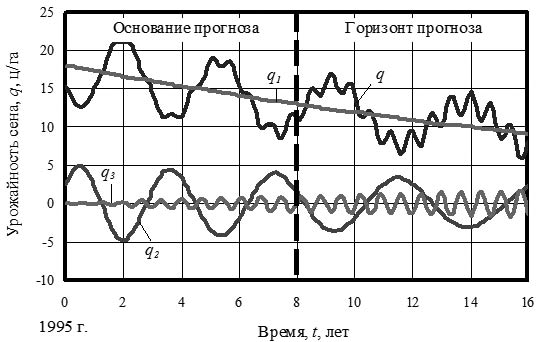
Рис. 14. Динамика урожайности сена на улучшенных сенокосах РМЭ в период 1995‒2011 гг., ц/га
Третья составляющая волны кризиса наращивается по амплитуде, а вторая составляющая - снижается. При этом тренд быстро снижает свои значения по первой составляющей экспоненциальной гибели. Этот факт показывает, что когда человек перестает вносить извне энергию в травяной покров, то культурный сенокос быстро превращается в исходное, то есть естественное для данных почвенных условий, состояние.
Прибавка урожай сена на улучшенных сенокосах, по сравнению с естественными сенокосами показывает (рис. 15), что она без участия человека быстро снижается и может стать даже отрицательной.
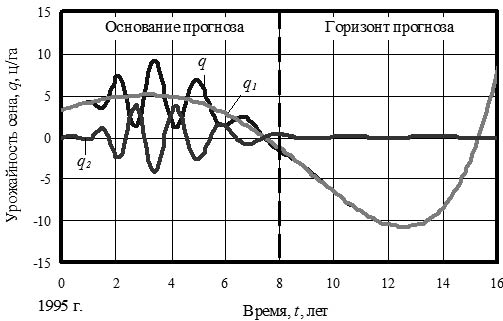
Рис. 15. Динамика прибавки урожая сена на улучшенных сенокосах, ц/га
Кризисная третья волновая составляющая затухает по амплитуде уже с 2004 года. При этом хорошим свойством становится и увеличение периода, то есть снижение частоты колебательного возмущения. Поэтому прогнозирование до 2011 г. выполняется по первым двум составляющим. Закон экспоненциального роста к 2011 г. начинает опережать и кризисный спад по закону показательного роста.
Значительное снижение урожайности сена с заброшенного сенокоса по сравнению с естественным травяным покровом, может привести к быстрой закустаренности территории. Такая ослабленная трава не сможет противодействовать проращиванию семян кустарниковых растений.
Коэффициент эффективности улучшению сенокосов изменяется по графикам, показанным на рис. 16.
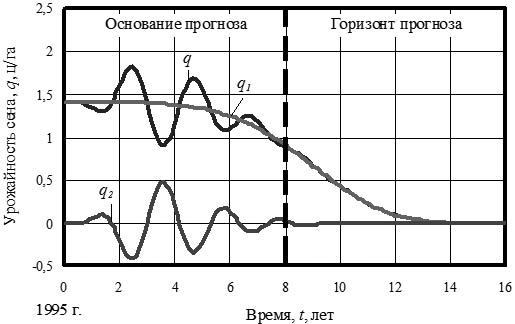
Рис. 16. Динамика коэффициента эффективности от улучшения сенокосов
Вторая кризисная составляющая затухает и поэтому коэффициент эффективности к 2009 году, если не будет улучшения, достигнет нуля.
Список литературы
- Реймерс, Н.Ф. Природопользование: Словарь-справочник / Н.Ф. Реймерс. - М.: Мысль, 1990. - 637 с.
- Мазуркин, П.М. Геоэкология: Закономерности современного естествознания: Научное изд. / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 336 с.
- Мазуркин, П.М. Закономерности устойчивого развития / П.М. Мазуркин. - Научное издание. - Йошкар-Ола: МарГТУ, 2002. - 302 с.
- Мазуркин, П.М. Рациональное природопользование: учебное пособие. В 3‒х ч. Ч. 1: Экологически ответственное землепользование / П.М. Мазуркин, С.Е. Анисимов, С.И. Михайлова; под ред. П.М. Мазуркина. - Йошкар-Ола: МарГТУ, 2006. - 176 с.
- Мазуркин, П.М. Математическое моделирование. Идентификация однофакторных статистических закономерностей: Учебное пособие / П.М. Мазуркин, А.С. Филонов. - Йошкар-Ола: МарГТУ, 2006. - 292 с.
- Республика Марий Эл: Статистический ежегодник / А.В. Целищев и др. - Часть 1. - Йошкар-Ола: ФСГС, 2004. - 342 с.
Статья подготовлена и опубликована при поддержке гранта 3.2.3/4603 МОН РФ
Библиографическая ссылка
Мазуркин П.М., Михайлова С.И. ПРОГНОЗИРОВАНИЕ УРОЖАЙНОСТИ СЕНА ОТ УЛУЧШЕННЫХ СЕНОКОСОВ // Успехи современного естествознания. 2010. № 11. С. 37-46;URL: https://natural-sciences.ru/ru/article/view?id=15185 (дата обращения: 12.02.2026).



