Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова

Пеньков Н.В.

Рассмотрен вариант синхронного деления клеток. Предложены кинетические уравнения, описывающие рост, размножение и гибель микроорганизмов с учетом как естественной смертности, так и внутривидовой борьбы. Рассматривается квазистационарный метод решения уравнения для определения плотности функции распределения микроорганизмов по возрастам. Предложен явный вид коэффициента диффузии в пространстве масс. Получено аналитическое решение в квазистационарном приближении для плотности функции распределения микроорганизмов по возрастам для случая, когда рост клетки пропорционален ее массе (объему).

Статья в формате PDF

279 KB

синхронное деление

внутривидовая борьба

квазистационарное приближение

функция распределения.

В настоящее время проблему, связанную с процессом роста, размножения и гибели микроорганизмов, целесообразно разделить на микрокинетическую и макрокинетическую. Микрокинетическая модель должна изучать рост, способ размножения и гибель отдельной изолированной клетки в зависимости от ее физиологического состояния, компонентов субстрата в ближайшем окружении клетки и скорости метаболизма в целях определения вероятности элементарных актов процесса роста, деления и гибели микроорганизма за единицу времени в заданном объеме системы.

В круг задач макроскопической модели следует включать вывод, исследование и разработку математических методов решения кинетических уравнений, описывающих эволюцию функции распределения популяции по массам (объемам) при заданном законе роста, размножения и гибели отдельной клетки.

Уравнения микрокинетики роста клетки имеют следующий вид:

- когда процесс микробиологического синтеза лимитируется биохимическими превращениями внутри клетки (Варфоломеев, Гуревич, 1999);

- если процесс микробиологического синтеза лимитируется диффузионным переносом питательных веществ к поверхности клетки.

Здесь

m₀ ≤ m(t) ≤ 2m₀, 0 ≤ t ≤ t_g,
 ψ(t) = ψ (C),

m(t) - масса отдельной клетки в момент времени t (m - детерминированная величина); t = t_g - время генерации (деления клетки); m₀ - масса клетки в момент времени t = 0; U(m, С) - скорость роста клетки; С - концентрация субстрата; µ₀ и К_с - постоянные величины; β - коэффициент массообмена;  где DM - коэффициент молекулярной диффузии, зависящий от температуры культуральной жидкости, d - толщина «пограничной пленки», зависящая от гидродинамической обстановки в окрестности клетки; S(t) - площадь внешней поверхности клетки в момент времени t. Предполагается, что при m(t) = 2m₀ происходит деление клетки на две дочерние.

Синхронное деление клеток. Согласно Дж. Бейли и Д. Оллису (1989) на ограниченном отрезке времени можно создать такие условия в системе, когда все клетки будут делиться синхронно. В этом случае при  имеют место следующие закономерности:

μ(t) =m₀2 ^τ, τ < 1;

 N(t) = N₀2 ^E(τ) , M(t) = M₀2^τ,

τ ≥ 0,

1. где M(t) и N(t) - масса и число клеток микроорганизмов в момент времени t>0 в единице объема системы M₀ = M(0), N₀ =N(0), Е(τ ) - целая часть от τ, равная наибольшему целому числу, не превосходящему τ. Так, Е(τ ) = 0 при 0<τ <1; Е(τ ) = 1 при τ = 1 + 0 и Е(τ ) = 0 при τ = l -0). Очевидно, что M(t)/N(t) = x(t) = m₀2 ^{τ -Е(τ )} - периодическая функция t с периодом Т = 1. Однако если, например, материнская клетка растет по закону , где u₀ - постоянная величина, то

m(t) = m₀(1+τ₁), τ₁<1,

τ₁=t/τ₀   τ₀=m₀/u₀, ,

x(t) = m₀[1+τ₁ - E(τ₁)], N(t) = N₀2 ^E(τ),

M(t) = x(t)N(t), τ >0.

2. По мере роста популяции ступенчатая зависимость числа клеток нарушается, что обусловлено стохастической природой роста и размножения микроорганизмов. Более того, как правило, популяция микроорганизмов состоит из громадного числа клеток, асинхронно делящихся и растущих с некоторыми индивидуальными скоростями в соответствии с их возрастом, со случайным изменением концентрации компонентов и метаболизма в ближайшем окружении отдельной клетки, каждая из которых представляет собой миниатюрный биореактор переменного объема, в котором непрерывно перерабатываются питательные вещества и синтезируются новые необходимые для жизнедеятельности микроорганизма.

Уравнения макрокинетики. При построении математической модели рассматриваемого процесса проблемами первоочередной важности являются выявление общих закономерностей и разработка математических методов описания эволюционных процессов, связанных с ростом, размножением и гибелью микроорганизмов в пространственно-однородных и неоднородных дисперсных системах, на основании единого логического подхода. Но в общем случае математическое описание процесса формирования спектра масс микроорганизмов в дисперсной среде чрезвычайно сложная задача. Однако если столь сложный процесс рассматривать как совокупность таких менее сложных («элементарных») процессов, участвующих в формировании спектра масс микроорганизмов, как непрерывный рост, размножение клеток, гидродинамическая обстановка в системе и др., то для математического описания сложного процесса целесообразно использовать принцип суперпозиции, сущность которого заключается в следующем.

Пусть  - скорость изменения плотности функции распределения числа микроорганизмов по массам (объемам) в рассматриваемой системе данный момент времени t, обусловленная «элементарным» процессом i-м, например ростом клеток, тогда скорость изменения плотности функции распределения для сложного процесса можно представить в виде суперпозиции скоростей для «элементарных» процессов (Пеньков, 1992), т.е.

.

Такой подход к математическому моделированию процессов, управляемых линейными и квазилинейными дифференциальными и интегро-дифференциальными эволюционными уравнениями математической физики, позволяет описать сложный процесс на основе кинетических уравнений, описывающих «элементарные» процессы.

Итак, пусть f(x,t) - плотность функции распределения (дифференциальная функция распределения) числа живых (способных к росту и размножению) микроорганизмов в момент времени t по массам х в единице объема дисперсной системы; f_p(x,t) - плотность функции распределения числа мертвых (не способных к росту и делению) клеток по массам х в единице объема системы в момент времени t;
Г(x,t)f(x,t) - число микроорганизмов массой х, погибших в единицу времени в единице объема системы в момент времени t естественной смертью;

 - число клеток массой х, погибших в единицу времени в единице объема системы в момент времени t вследствие внутривидовой борьбы. Здесь Г(x,t) и G(x,ζ,t) - заданные функции своих аргументов. Тогда с учетом изложенного выше для пространственно-однородных систем, когда клетки распределены равномерно по объему, можно получить следующие квазилинейные интегро-дифференциальные уравнения, описывающие рост, размножение и гибель микроорганизмов:

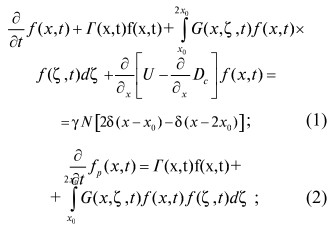
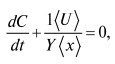 (3)

где U = U(x,C,t) - скорость роста клеток массой х в момент времени t;

D_c = D_c(x,C,t) - стохастический параметр (D_c - коэффициент диффузии в пространстве масс); γ - удельная скорость поступления в систему микроорганизмов массой х₀, образовавшихся при делении клеток массой 2х₀; δ(z) - дельта-функция Дирака от z; - знак среднего значения от указанной величины; Y - экономический коэффициент;  и - соответственно масса N живых и N_p мертвых клеток в единице объема системы в момент времени t.

Система уравнений (1)-(3) незамкнута. Для получения дополнительной информации умножим уравнения (l) и (2) на х и проинтегрируем по х от х=х₀ до х=2х₀. В результате получим уравнения для определения M(t) и М_p(t):

 (4)

 (5)

Уравнения (l)-(5) следует еще дополнить законом сохранения вещества:

M(t) + M_p(t) + YC(t) = M₀+YC₀, M_p(0) = 0, (6)

где С₀ и М₀ -значения M(t) и C(t) при t = 0. Для решения уравнений (1)-(6) необходимо еще задать начальные и граничные условия:

Начальные условия:

f(x,0)= f₀(x) f_р(х,0)=0, М(0) = М₀,
М_р(0) = 0, С(0) = С₀,

где f₀ (x), М₀ и С₀ - заданные величины

Граничные условия:

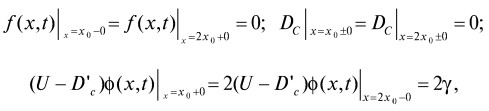
3. где  предполагается, что U > D´_c для всех х ∈ [х₀,2х₀].
4. Уравнение (1) заменой искомой функции f(x,t) на F(x,t) по формуле

f(x,t) = [θ(х -х₀) -θ (х - 2x₀)]F(x,t), (7)

5. с учетом того, что θ (z)=0 при z<0 и θ (z) = 1 при z>0,

dθ /dz=δ(z), zδ(z) = 0, f(x,t) δ (x - z) = f(z,t) δ(x - z),

где δ(z) - дельта-функция Дирака, преобразуется в уравнение

 (8)

решение которого должно удовлетворять начальному F(x,0) = F₀(x) и граничному условию

 (9)

Аналитическое решение полученной системы уравнений представляет значительные трудности. Очевидно, что оно упрощается, если имеют место равенства:

Г(х,t)=Г₀, G(x,ζ,t)=G0, U(x,C,t)=x ψ(C),

где ψ(0)=0, Г₀ и G₀ - постоянные величины, а ψ (С) - заданная функция своего аргумента. В этом варианте решение системы уравнений (2)-(6) можно представить в следующем виде:

M(C)=M₀+Y(C₀ -C) -M_p(C), C≥C*: (10)

 (11)

6. где  Из условия М(С) = 0 при С = С* следует уравнение для определения величины С = С*:

M₀+Y(C₀-C*) = M_p(C*) (12)

Зная зависимость функции М от С, согласно уравнению (3), можно найти C(t):

 (13)

Выражения (10)-(13) при G₀ = 0 были получены ранее (Пищиков, Пеньков, 2005).

Анализ. Из уравнения

следует, что при ψ(С) > Г₀ + αМ функция M(t) возрастает от М = M₀ до М=М_mах, а при ψ(С)<Г₀ +αМ - убывает до М = 0. Следовательно, при ψ (С_λ) = Г₀+ αМ(С_λ) функция M(t) достигает своего максимального значения. В свою очередь функция М(t) возрастает от нуля до М_p=М₀ + Y(C₀ - С*), причем ее график имеет точку перегиба при С=С_λ.

Из уравнения (12) следует, что при гибели клеток существует пороговая минимальная концентрация субстрата, ниже которой клеточный прирост массы живых клеток прекращается.

Однако следует заметить, что для определения величины C=C* согласно уравнениям (11) и (12), необходимо знать величину , которую, в свою очередь можно найти только в случае, если известна функция . Очевидно, что уравнение для определения искомой функции P(x,t) можно получить, используя уравнения для функций F(x,t) и N(t):

 (14)

 (15)

Действительно, так как F(x,t) = P(x,t)N(t), то, исключая величину N(t) из уравнения (14), получим уравнения для искомых функций P(x,t) и :

 (16)

 (17)

Уравнение (14) справедливо и в том случае, когда , где φ(х) - заданная функция.

Для решения уравнения (16) используем квазистационарное приближение, положив В этом приближении

 (18)

Уравнение (16) значительно упрощается, когда φ(х)=х. В этом варианте в квазистационарном приближении, если левую и правую части этого уравнения умножить на х и проинтегрировать по х от х=х₀ до х=2х₀, используя соответствующие граничные условия, то при D_c(x, t) = U(x, t)b(x) получим достаточно компактное уравнение

 (19)

где 

Перейдем к безразмерной переменной х= х₀z. В этом случае при

 (20)

уравнение (19) преобразуется к виду

 (21)

Решение которого, удовлетворяющее граничным условиям:

 (22)

представимо в виде

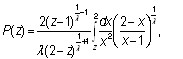 0<λ <1; (23)

 λ=0. (24)

Так, =2x₀ ln2 при λ=0, а при λ>0 справедливо неравенство

 (25)

Далее, так как

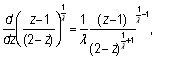
то легко показать, что функция P(z) нормирована на единицу.

В заключении следует отметить, что предложенные уравнения для описания роста, размножения и гибели микроорганизмов в закрытых пространственно-неоднородных дисперсных системах легко обобщаются на открытые системы с истоком и внешним источником микроорганизмов (см., например, Пеньков, Пищиков, 1999).

Список литературы

1. Варфоломеев С.Д., Гуревич К.Г. Биокинетика. Практический курс. М.: ФАИР-ПРЕСС, 1999. - 720 с.
2. Бейли Дж., Оллис Д. Основы биохимической технологии. Ч. I, 1989. - С. 464-457.
3. Пеньков Н.В. Коагуляционные процессы в дисперсных системах: Дис. ... докт. физ.-мат. наук. М.: НИИФХИ им. Карпова, 1992. - 342 с.
4. Пищиков Г.Б., Пеньков H.В. К кинетике роста, размножения и гибели микроорганизмов // Хранение и переработка сельхозсырья. - 2005. - №5. - С. 19-21.
5. Пеньков Н.В., Пищиков Г.Б. Кинетическая модель процесса роста, размножения и гибели дрожжевых клеток // Хранение и переработка сельхозсырья. - 1999. - №7. - С. 61-63.

Библиографическая ссылка