В предыдущих работах авторов (например [1, 2]) были разработаны модели иерархических систем для категории пожилых людей. В данной работе исследуется состояние иерархических систем для данной категории в различные отрезки времени.
Современная демографическая ситуация в Иркутской области, как и в целом по Российской Федерации, характеризуется динамичным увеличением доли лиц пожилого возраста. Начиная с 1995 года доля пожилых граждан в составе населения Российской Федерации превышает 20 %. Они сталкиваются с большим количеством проблем, которые самостоятельно решить не могут, отсюда имеет место большое количество обращений за помощью в государственные органы власти. Для решения проблем необходимо проведение мониторинга обращений, для этого целесообразно построить модель, с помощью которой можно проследить изменения количества состава категорий населения.
В Иркутской области также наблюдается устойчивый рост в общем составе населения доли граждан пожилого возраста с 16,7 % в 2002 году до 18,6 % в 2010 году. В тоже время имеются некоторые категории населения, численность которых в силу естественных причин уменьшается. Это - инвалиды Великой Отечественной войны, участники Великой Отечественной войны, труженики тыла, реабилитированные лица и признанные пострадавшими от политических репрессий.
Для каждой страты в иерархической системе можно определить различные количественные показатели (численность, выплаты, льготы и т.д.), которые с течением времени t могут изменяться, уменьшаться или увеличиваться. Таким образом, будет изменяться и сама иерархическая система. Поэтому имеет смысл ввести понятие динамической иерархической системы, то есть такой, в которой количественные показатели страт будут зависеть от времени.
Определение. Пусть задана иерархическая система I и A - некоторая страта этой системы и определена функция f: I×T → S, где T - множество вещественных чисел, S - некоторое множество (числовое, символьное, векторное и т.д.), I×T - декартово произведение множеств I и T. Тогда пара <I, f> называется динамической иерархической системой.
В качестве примера страты из такой иерархической системы мы рассмотрим изменение численности страты «труженики тыла». Для этого рассмотрим данные, приведенные в следующей таблице.
|
Год |
2005 |
2006 |
2007 |
2008 |
|
Численность страты труженик тыла сi |
2951 |
2910 |
2864 |
2840 |
По данной таблице построим функцию для данной страты (см. [1]), а именно интерполяционный многочлен Лагранжа, показывающий непрерывные изменения численности с 2005 по 2008 годы. Для этого по приведенной таблице построим нормализованную таблицу, в которой вместо значения численности запишем относительную убыль Δi =сi - 2800.
|
Год |
2005 |
2006 |
2007 |
2008 |
|
Относительная убыль Δi |
151 |
110 |
64 |
40 |
Тогда многочлен Лагранжа, построенный по нормализованной таблице, выглядит так:
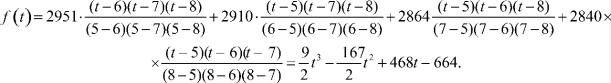
Функция f(t) от времени t, определенная на данной страте, позволяет отслеживать количественные изменения страты в любой момент времени t от 2005 до 2008 года, но в тоже время эта функция не позволяет прогнозировать значения f(t) в последующие годы. Действительно, f(9) = 65, а реальное значение Δi за 2009 год равно 9. Для прогнозирования изменения страт будут предложены некоторые другие функции в последующих работах.
Список литературы
- Клейменов В.Ф., Суровцева Н.Н. Функции для иерархии категорий пожилых людей // Фундаментальные исследования. - 2008. - № 10. - С. 75.
- Суровцева Н.Н., Клейменов В.Ф. О модулярных решетках в иерархии страт // Успехи современного естествознания. - 2010. - № 9. - С. 204-205.
Библиографическая ссылка
Суровцева Н.Н., Клейменов В.Ф. ДИНАМИЧЕСКИЕ ИЕРАРХИЧЕСКИЕ СИСТЕМЫ В СОЦИАЛЬНОЙ РАБОТЕ // Успехи современного естествознания. 2011. № 5. С. 139-140;URL: https://natural-sciences.ru/ru/article/view?id=21508 (дата обращения: 03.03.2026).



