Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова

Жижин К.С. 1

---

1 ГБОУСПОРО «Ростовский базовый медицинский колледж»

В работе рассматриваются приемы дискриминации признаков производственных травм с использованием модуля «Дискриминантный анализ» статистического софта «Statistica» v.6. Отражена простота анализа и получения выводов. Рекомендации могут быть реализованы специалистами, чей математический багаж не превышает базиса средней общеобразовательной школы.

Статья в формате PDF

654 KB

трудовой процесс

дискриминация травмы

Трудоохранные мероприятия в современных условиях не могут не базироваться на переработке достаточно плотного потока статистических данных. Без них невозможно прогнозировать ситуацию, стоить стратегию улучшения условий труда. В череде этих проблем самая существенная – классифицирование производственных травм, профессиональных заболеваний и отравлений при формировании динамического ряда. Лет 15–20 назад такая работа требовала привлечения труда профессионалов-программистов, занимала много времени на обработку и анализ полученных результатов. Современные статистические софты в значительной мере облегчили эту работу специалистам трудоохранных служб, поскольку подоплека их интуитивно понятна даже человеку с математическим базисом на уровне 10–11 классов средней общеобразовательной школы.

Материалы и методы исследования

Дискриминантный анализ, применение которого мы демонстрируем в данном сообщении – достаточно сложный раздел математической статистики. И, тем не менее, с помощью модуля «Дискриминантный анализ» из американского статистического софта «Statistica» v.6 мы хотели бы показать насколько просто провести процесс дискриминации. Примером в данном сообщении служит классификация производственных травм по тяжести.

Результаты исследований и их обсуждение

Данная выборка включает 11 единиц наблюдений, отобранных случайным образом из совокупности в 100 единиц. Травмы будем классифицировать, опираясь на следующие дискриминационные признаки: количество дней нетрудоспособности работника из-за одной травмы, число травм, случившихся у него в течение года, расходы на лечение в тыс. руб. (в расчете на одну травм), индекс травмирования, то есть отношение числа травм к числу дней нетрудоспособности, табл. 1. Подразумевается, что программа «Statistica» v.6. уже установлена, поэтому обходим процедуру её инсталляции на жесткий диск компьютера.

На верхней панели окна щелкаем левой кнопкой «мыши» на слове Анализ, отыскиваем Многомерный разведочный анализ, в нем – Дискриминантный анализ (рис. 1).

Во вкладке Быстрый выбираем Дополнительные параметры (пошаговый анализ). После нажатия на кнопку Переменные отобразится стандартное диалоговое окно Выбор переменных (его мы не показываем) (рис. 2). В этом окне укажем группирующую переменную и независимые переменные, которые должны быть использованы для дискриминации типа травм. В нашем случае группирующим признаком будет тяжесть травмы.

Нажимаем кнопку ОК, и переходим к следующему этапу: Результаты.., рис. 3. Просмотр результатов дискриминантного анализа, и классификация наблюдений начинаются с верхней части. В белом прямоугольнике, представлены значения самого существенного показателя дискриминации – лямбды Уилкса, пределы её изменений: 0–1. В нашем случае значение лямбды достаточно мало – 0,0026 (Суть в том, что, если это значение близко к нулю, то дискриминация прошла успешно, если же близко к единице, то дискриминация сомнительна) (рис. 3). Помимо этого, полученный в опыте, своеобразный показатель достоверности вывода, критерий Фишера «F» также высок – 23,2, почти в три раза перекрывает свое стандартное значение – 8,10 (в скобках).

Таблица 1

Классификация травм

Многомерный разведочный анализ Дискриминантный анализ

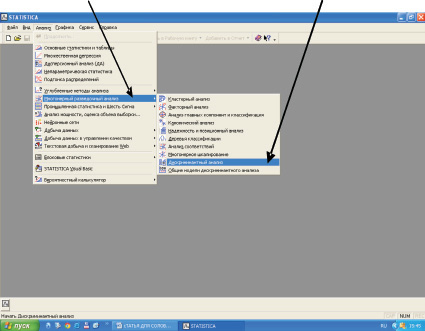
Рис. 1. Окно Анализ программы «Statistica» v.6

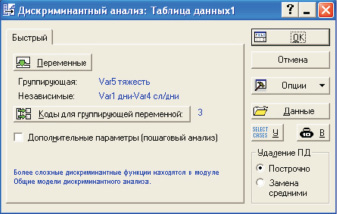
Рис. 2. Окно Дискриминантный анализ программы «Statistica» v.6

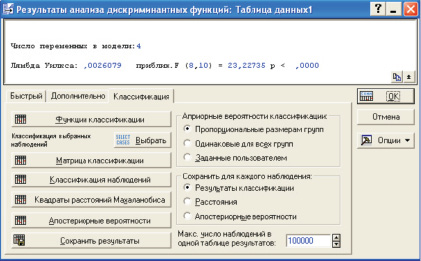
Рис. 3. Окно Результаты анализа

Для подтверждения и закрепления факта дискриминации определим еще несколько показателей. На первом месте – Расстояние Махаланобиса, которое является мерой близости отдельно взятых наблюдений и центром каждой совокупности, из включенных в процесс дискриминации. Чем ближе наблюдение к центроиду конкретной совокупности, тем в большей степени можно быть уверенным, что наблюдение извлечено именно из неё. Расстояние Махаланобиса может быть рассчитано при нажатии на кнопку Квадраты расстояния Махаланобиса во вкладке Классификация. Дифференциация случаев травмирования по этому признаку отражена в табл. 3 (цветом выделены статистически значимые показатели).

Кроме Расстояния Махаланобиса можно вычислить еще и условную (или апостериорную) вероятность принадлежности наблюдения к определенной совокупности. Её условность в том, что она зависит от знания исследователем значений переменных в модели. Этот показатель получают, нажав на кнопку Апостериорные вероятности. В данном примере точность классификации очень высока, даже с учетом того, что это апостериорная классификация. К слову сказать, такая точность редко достигается и редко, когда нужна.

Таблица 2

Квадраты расстояний Махаланобиса

Для проверки работоспособности представленной модели с учетом вероятностей в исходную табл. 1 введем переменные под № 12, 13, 14 с их значениями, табл. 3

Таблица 3

Проверка работоспособности методики анализа

При повторении анализа машина мгновенно классифицирует травмы по тяжести, отнеся 12 и 13 случаи к легким, а 14 – к среднетяжелым травмам, табл. 4. Примечательно, что классификация наблюдений по вероятностным признакам оказалась гораздо показательней расчета квадратов Расстояний Махаланобиса: дифференциация в данном случае равна 1,0 или 100 %.

Таблица 4

Апостериорные вероятности травмирования

Выводы

Хотя данный пример нами сознательно упрощен, тем не менее, хорошо иллюстрирует основную идею дискриминации. Для «перестраховки» в ответственных случаях следует проводить дискриминацию в два этапа: сначала построить функции классификации и только потом проводить оценку их качества.

При использовании данного вида анализа необходимо учитывать несколько ограничений: нормальность и линейность эмпирического распределения, однородность дисперсий и ковариаций сравниваемых совокупностей. Однако, как показала наша практика, методика достаточно «терпима» к отклонениям от этих условностей.

Библиографическая ссылка