С каждой акцией для акционера связано по меньшей мере два фактора – доход и риск. Вкладывать все средства в акции одной компании неразумно, поэтому основной задачей инвестора является формирование инвестиционного портфеля, состоящего из акций различных компаний. Доход по каждой акции в портфеле определяется ценой акции как на момент покупки, так и ее будущей ценой на момент подведения итогов. Причем будущие цены и доходности по акциям являются неопределенными.
В настоящее время существует множество портфельных моделей – Г. Марковица, У. Шарпа, САРМ и их многофакторные модификации [1, 2], которым, вместе с тем, присущи принципиальные недостатки, существенно ограничивающие их адекватность и применимость на практике. К ним относятся:
– основной акцент делается только на риски, то есть убытки по каждой акции, в то время как ожидание повышенной доходности акций в будущем, то есть шансы, и является главной целью инвестора;
– отождествление риска с дисперсией разброса доходности акций и изменчивостью дохода, невалидно [3].
– полагают, что доход на акцию, риск, ковариация между акциями в прошлые периоды, полностью сохранятся и в будущем;
– модели портфелей не учитывают изменений курсов акций, их рисков и ковариаций из-за изменчивости экономики, социального положения, как в обществе, так и в самой компании.
В статье предлагается математическая модель формирования оптимального инвестиционного портфеля опирающаяся как на данные по доходности акций за прежние периоды, так и на прогнозные значения доходности в будущем, а также на анализ не только возможных убытков по акциям, то есть рисков, но и возможных прибылей, то есть шансов. Полученная математическая модель является оптимизационной и относится к классу задач линейного программирования.
Математическая модель формирования инвестиционного портфеля
Математическая модель формирования инвестиционного портфеля ценных бумаг основывается на следующей концепции:
• будущий доход по любой акции является неопределенным событием. Это означает, что в будущем финансовый итог по акции может оказаться прибылью, которую мы называем шансами или убытком, которые мы называем рисками;
• количественная мера i-го риска (ri) и шанса (сhi) определяется как произведение материальной меры прибыли (Mchi) или убытка (Mri) и меры возможной актуализации (МВА) в будущем события-прибыли (Pchi) или события-убытка (Pri). Отметим, что существующие портфельные модели, трактуют риск по акциям как дисперсию случайной величины доходности по данным за прошлые периоды, которые, однако, не имеют никакого отношения ни к риску, ни к шансу;
• данные по поведению, прибылям и убыткам каждой акции за прошлые периоды, также важны как и их прогнозируемые значения.
При покупке акций разумный инвестор оценивает акции конкретной компании с точки зрения во-первых, будущего роста цены и, во-вторых, превышения ожидаемого дохода над альтернативным доходом, который получил бы инвестор, воспользовавшись альтернативными формами получения прибыли, например, такими, как проценты по облигациям, банковские проценты по вкладам и др.
Рассмотрим инвестиционный портфель, содержащий n видов акций n различных компаний.
Полной характеристикой i-й акции, показывающей соотношение между ее полными шансами (Ci) и рисками (Ri), является комплексный показатель C&Ri:
C&Ri = βСCi – βRRi, (1)
где βС и βR – коэффициенты относительной важности шансов и рисков, отражающие субъективное отношение конкретного субъекта (инвестора, эксперта) к шансам и рискам. Коэффициенты важности βС и βR отражают склонность субъекта, принимающего решение, к осторожности, к рискованности, или его нейтральное отношение к шансам/рискам по акциям.
Перед тем как решать какие акции включать в портфель необходимо сначала обратить внимание на знак комплексного показателя (1) C&Ri. Если комплексный показатель для данной акции неотрицателен (C&Ri ≥ 0), то такая акция может быть включена в инвестиционный портфель. В противном случае, если окажется, что ожидаемые убытки превышают ожидаемые прибыли, то есть C&Ri < 0, то такую акцию включать в портфель не следует.
Зная комплексный показатель C&Ri для каждой i-й акции, i = 1, 2, …, n, можно вычислить комплексный показатель C&Ri инв. портф для всего инвестиционного портфеля, содержащего n видов акций:
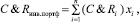 (2)
(2)
где xi = cimi/К – доля от капитала инвестора К, вложенная в покупку акций i-й компании в количестве mi по цене ci за одну акцию (0 ≤ xi ≤ 1, i = 1, 2, …, n), причем для всего инвестиционного портфеля выполняется балансовое равенство x1 + x2 + … + xn = 1 [1].
Разработанная математическая модель формулируется следующим образом: найти значения долей капитала xi, i = 1, 2, …, n, которые следует вложить в различные акции, чтобы комплексный показатель C&Rинв.портф был максимальным, полный желаемый доход всего инвестиционного портфеля Iинв.портф был не меньше желаемого дохода I0 ≥ Iа. Таким образом, математическая модель, описывающая формирование оптимального инвестиционного портфеля, относится к классу задач линейного программирования и имеет вид:
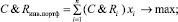 (3)
(3)
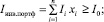 (4)
(4)
x1 + x2 + … + xn = 1; (5)
0 ≤ xi ≤ 1, i = 1, 2, …, n; (6)
x1 ≤ s1, x2 ≤ s2, …, xn ≤ sn, (7)
где s1, s2, …, sn – ограничения на доли x1, x2, …, xn капитала, которые инвестор направляет на покупку акций i = 1, 2, …, n; Ii – желаемые значения доходностей каждой акции i = 1, 2, …, n; I0 – минимальное желаемое значение доходности всего инвестиционного портфеля; С и R – полные шансы и полные риски по данной акции, равные сумме произведений материальных мер и мер возможной актуализации шансов и рисков, то есть
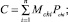
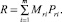
Инвестор может, вообще говоря, формировать различные инвестиционные портфели, отличающиеся друг от друга, различными наборами акций. Для каждого k-го варианта определяется свой оптимальный инвестиционный портфель с оптимальной структурой (x1, x2, …, xn)k и значением полного ожидаемого дохода Iинв.портф(k) Тогда глобальное оптимальное решение, отвечающее наилучшему оптимальному инвестиционному портфелю среди всех сформированных вариантов инвестиционных портфелей, будет соответствовать такому портфелю, который имеет наибольшее значение полного ожидаемого дохода
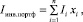
то есть
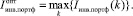
Оценка мер возможной актуализации шансов и рисков
Будем с каждой акцией связывать два события, которые после приобретения данной i-й акции могут актуализироваться к моменту подведения финансовых итогов по доходности акций:
• шанс (chi) – превышение будущего дохода по каждой i-й акции Ii = (ci’ – ci)/ci, (ci’ и ci – цена одной акции через некоторый период времени и в момент покупки соответственно) над величиной альтернативного дохода Iа, который мог бы получить инвестор, вложив ту же сумму (ci) в альтернативные источники дохода. При актуализации шанса выполняется неравенство Ii ≥ Iа, %;
• риск (ri) – будущий доход на i-ю акцию Ii = (ci’ – ci)/ci не превысит ее альтернативного значения Iа, то есть Ii ≤ Iа.
Меры возможной актуализации шансов и рисков вычисляются с помощью следующего метода. Актуализация в будущем шанса или риска по каждой акции, носит неопределенный характер, который обусловливается неопределенностью экономической и социальной составляющих окружающей среды, а также поведением акции в прошлые периоды. Обозначим l возможных будущих состояний экономики как С1, С2, …, Сl, а k возможных будущих социальных состояний, как S1, S2, …, Sk. Будем также полагать, что экономические и социальные состояния окружающей среды независимы между собой, независимы в своих совокупностях и образуют каждые полные группы событий.
Будущее неопределенное событие, состоящее в актуализации шанса chi или риска ri каждой i-й акции, может наступить совместно с одним из состояний экономики С1, С2, …, Сl и одним из социальных состояний общества S1, S2, …, Sk. Кроме того, следует учитывать имеющиеся статистические данные по поведению акций за прошлые периоды; причем поведение акции в данной модели заключается в наступлении либо шанса, либо риска. Обозначим шанс и риск, имевшие место в прошлом, как 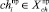 и
и 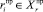 , где
, где 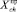 и
и 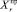 – множества шансов и рисков за прошлые периоды, релевантных данным акциям. Это означает совместное наступление (пересечение) множеств событий ∪Cj, ∪Sq и
– множества шансов и рисков за прошлые периоды, релевантных данным акциям. Это означает совместное наступление (пересечение) множеств событий ∪Cj, ∪Sq и 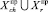 , то есть (chi, ∪Cj, ∪Sq,
, то есть (chi, ∪Cj, ∪Sq, 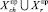 ) и (ri, ∪Cj, ∪Sq,
) и (ri, ∪Cj, ∪Sq, 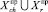 ). Тогда значения МВА шанса chi и риска ri для i-й акции Pchi = P(chi, ∪Cj, ∪Sq,
). Тогда значения МВА шанса chi и риска ri для i-й акции Pchi = P(chi, ∪Cj, ∪Sq, 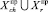 ) и Pri = P (ri, ∪Cj, ∪Sq,
) и Pri = P (ri, ∪Cj, ∪Sq, 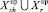 ) могут быть записаны с использованием условных вероятностей в следующем виде:
) могут быть записаны с использованием условных вероятностей в следующем виде:
Pchi = P(∪Cj,∪Sq, 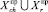 )∙P(chi|∪Cj, ∪Sq,
)∙P(chi|∪Cj, ∪Sq, 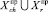 ), (8)
), (8)
Pri = P(∪Cj, ∪Sq, 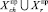 )∙P(ri|∪Cj, ∪Sq,
)∙P(ri|∪Cj, ∪Sq, 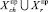 ). (9)
). (9)
Обобщенные выражения (8) и (9) могут быть конкретизированы, если воспользоваться концепцией автора о трех иерархических уровней шансов и рисков [4]. Согласно этой концепции риски и шансы, в зависимости от степени неопределенности будущих результатов действий или принятых решений, могут быть отнесены к одному из трех уровней – оперативному, тактическому и стратегическому.
Оперативный уровень характеризуется тем, что длительность периода времени, между моментом покупки акции и моментом подведения финансовых итогов (назовем его период актуализации рисков/шансов), является незначительной (один-несколько дней), по крайней мере, настолько, чтобы в течение этого времени можно было пренебречь изменениями в экономическом и социальном состояниях окружающей среды. В этом случае экономическое и социальное состояния окружающей среды можно считать неизменными и равными таковым на момент покупки акции. Это означает, что характеристики рисков и шансов по акциям на оперативном уровне за прошлые периоды можно экстраполировать практически без изменения на конец периода оперативного уровня. Тактический уровень характеризуется тем, что период актуализации является, по сравнению с оперативным уровнем, более длительным (несколько недель, но не более года), так что изменениями в экономике пренебрегать уже нельзя, однако значимых изменений в социальном, в том числе и политико-правовом, состояниях общества, не происходит. Это означает, что при оценке рисков и шансов на тактическом уровне следует учитывать только изменения в экономике. Отметим, что на тактическом уровне экономические изменения могут быть и незначительными, но тем не менее изменения в рисках/шансах акций могут быть существенными и их следует учитывать. На стратегическом уровне период актуализации рисков/шансов является столь длительным (от нескольких месяцев, до нескольких лет), что за это время могут произойти любые изменения как в экономическом, так и в его социальном состояниях, что неминуемо скажется курсах акций любой компании. Причем эти изменения могут носить самый неожиданный и трудно прогнозируемый характер. Поэтому на стратегическом уровне риски и шансы по акциям будут испытывать на себе влияние изменений всех факторов неопределенности (экономический, социальный, включая политико-правовой).
Применяя концепцию иерархических уровней рисков/шансов и учитывая, что множества состояний экономики ∪Cj, социального положения ∪Sq и множество шансов и рисков за прошлые периоды 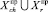 , независимы между собой и каждое из них образует полную группу несовместных и независимых в совокупности событий, можно получить конкретный вид общих выражений (8) и (9).
, независимы между собой и каждое из них образует полную группу несовместных и независимых в совокупности событий, можно получить конкретный вид общих выражений (8) и (9).
Выводы
Полученная в статье математическая модель оптимального инвестиционного портфеля отличается от существующих моделей (Г. Марковица, У. Шарпа, САРМ и т.д.) и является более реалистичной и учитывающий непосредственные интересы инвестора. Модель является оптимизационной, относится к классу моделей линейного программировании и ее решение может быть без труда найдено с помощью современных компьютерных технологий, в частности, средствами MS Excel.
Работа поступила в редакцию 27.11.2012.
Библиографическая ссылка
Мадера А.Г. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ // Успехи современного естествознания. 2012. № 12. С. 109-112;URL: https://natural-sciences.ru/ru/article/view?id=31210 (дата обращения: 07.03.2026).



