Известны два основных вида последовательностей точек (итерационная последовательность и канторово множество), представители которых в 1D-пространстве обладают свойствами фрактальных структур и имеют размерность меньше единицы [1, 2]. Для формирования других фрактальных структур в 1D-пространстве, связанных соотношениями гомологии, будем использовать методики, описанные в [3-7].
Итерационная последовательность uk точек может быть получена по итерационному алгоритму, реализующему последовательность отображений Ak начальной точки u0 с помощью операции итерации uk+1 = Akuk, где показатель итерации k = 0, 1, 2, 3…∞. При u0 = 0,5 имеем uk+1 = Ak(12)k , где Ak = 0,5 [2].
В общем случае, если u0 = n/(n+1), то последовательность с начальной точкой u0 = 0,5 можно рассматривать как первый член одномерного гомологического ряда итерационных последовательностей unk = [n/(n+1)]k, где n = 0, 1, 2, 3…∞. Предельное значение каждой последовательности lim unk = (1– 2un) = = (3n+1)/(n+1). В этом случае их фрактальные размерности определяются следующим образом: Dim(unk) = ln(n+1)/ln(3n+1) < 1. В более общем случае можно рассматривать двумерные гомологические ряды итерационных последовательностей точек вида unmk = [n/(n+m)]k, для которых Dim(unmk) == ln(n+m)/ln(3n+m), где m = 1, 2, 3…∞.
Канторово множество – совершенное множество точек на отрезке [0,1] прямой, которое может быть получено путем последовательного и неограниченного удаления средней трети отрезка [0,1], затем – средних третей отрезков [0,1/3] и [2/3,1] и т.д. Данное множество – результат бесконечного итерирования интервалов вида Vk = (1/3)k. Генератор фрактальной структуры C(1/3){1-}, фрактальная размерность канторова множества равна 0,6309.
В общем случае данная фрактальная структура может быть первым членом одномерного гомологического ряда структур с генераторами вида C(n/n+2){1-}, где n = 1,2,3… ∞. Фрактальные размерности этих структур Dim C(n/n+2) = ln2/ln(n+2). В более общем случае можно рассматривать генераторы C(n/n+2m){1-} фрактальных структур, которые образуют двумерный гомологический ряд вида Vnmk = (n/(n+2m))k, где m = 1,2,3… ∞. Размерности данных фрактальных структур определяются по формуле Dim C(n/n+2m) = ln2m/ln(n+2m) < 1.
Некоторые генераторы возможных фрактальных структур I(n/(n+1)){0+} и C(n/(n+2)){1-} в 1D-пространстве для представителей первых пяти одномерных гомологических рядов последовательностей точек un1k и канторовых множеств vn1k изображены на рисунке (а и б). На этом рисунке представлены закономерности изменения фрактальной размерности unmk (в) и vnmk (г) при некоторых фиксированных значениях параметра m от порядкового номера n в рядах структур.
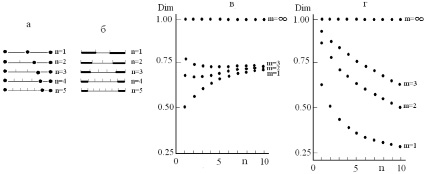
Генераторы фрактальных структур I(n/(n+1)){0+} (а) и C(n/(n+2)){1-} (б). Изменение фрактальной размерности итерационных последовательностей точек unmk (в) и канторовых множеств vnmk (г) от порядкового номера n в гомологических рядах структур I(n/(n+m)){0+} (а) и C(n/(n+2m)){1-}, соответственно
Очевидно, что для каждого фиксированного n при m → ∞ размерности всех анализируемых видов фрактальных структур монотонно приближаются к 1. Формально при бесконечно больших значениях параметра m эти фрактальные структуры представляют собой квазикомпактное множество точек и имеют размерности, близкие к значению 0,9999.
Для итерационных последовательностей точек для каждого фиксированного m и n → ∞ размерность Dim(unmk) → 1 (например, при m = 1 для значений параметра n = 1, 103 и 106 величины соответствующих фрактальных размерностей 0,5, 0,863 и 0,926). Для гомологических рядов канторовых множеств для фиксированного m размерность Dim(Vnmk) при n → ∞ закономерно снижается до минимально возможного значения (например, при m = 1 для значений параметра n = 1, 103 и 106 величины соответствующих фрактальных размерностей 0,6309, 0,0999 и 0,0499).
Таким образом, в 1D-пространстве, в соответствии с основными принципами, сформулированными в [3-7], могут быть сформированы фрактальные структуры I(n/(n+m)){0+} и C(n/(n+2m)){1-} – представители гомологических рядов итерационных последовательностей точек unmk (в) и канторовых множеств Vnmk (г). Данные фрактальные структуры характеризуются размерностями практически во всем диапазоне значений от 0,0001 до 0,9999.
Библиографическая ссылка
Иванов В.В. ФОРМИРОВАНИЕ ФРАКТАЛЬНЫХ СТРУКТУР НА ОСНОВЕ ИТЕРАЦИОННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ И КАНТОРОВА МНОЖЕСТВА ТОЧЕК С ЗАДАННЫМИ ХАРАКТЕРИСТИКАМИ В 1D-ПРОСТРАНСТВЕ // Успехи современного естествознания. 2013. № 8. С. 136-137;URL: https://natural-sciences.ru/ru/article/view?id=32748 (дата обращения: 11.03.2026).



