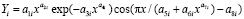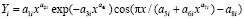Для снижения линейной эрозии почвы оврагами применяют растения. Цель исследования – изучение формы комля деревьев, растущих в овраге, для выявления закономерностей взаимодействия между древесными растениями и склоном. Объектами исследования были выбраны березы на склоне лесного оврага около деревни Ямолино Горномарийского района Республики Марий Эл. Эксперименты проведены летом 2011 года (табл. 1) на 30 березах.
В табл. 1 были приняты следующие условные обозначения: P1.3, D1.3 – диаметр и периметр ствола березы на высоте 1,3 м от корневой шейки, см; Pкш – периметр сечения ствола на корневой шейке, см; Ph – периметр комля березы в сечении над точкой пересечения поверхности почвы с вертикальной осевой линией комля дерева, см; h – высота комля от корневой шейки до центральной точки пересечения поверхности почвы с вертикальной осевой линией комля дерева, см; H, Hкр – высоты дерева и кроны, измеренные эклиметром, м; P1.3/ D1.3 – коэффициент формы поперечного сечения ствола дерева на высоте 1,3 м; Pкш/ P1.3 – относительный сбег поперечного сечения ствола дерева от корневой шейки до стандартной высоты 1,3 м, то есть коэффициент закомелистости ствола дерева; Ph/P1.3 – относительный сбег комля дерева от сечения на высоте комля до стандартной высоты.
Ранее нами была доказана [1-5] волновая теория развития и роста деревьев. Поэтому проведена идентификация общей биотехнической закономерности
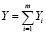 ,
, 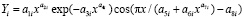 , (1)
, (1)
где Y – показатель, в нашем примере любой из трех отношений между периметрами сечений комля и ствола дерева, i – номер члена общей формулы (1), m – количество составляющих общей формулы, шт., x – любой из семи влияющих переменных дерева и комля березы, a1…a8 – параметры одного члена формулы (1), физически представляемого как асимметричный вейвлет-сигнал с переменными амплитудой и частотой колебательного возмущения совокупности (популяции) из 29 берез.
Таблица 1
Параметры деревьев и периметры сечения комля с их отношениями
|
№ п/п |
D1.3, см |
h, см |
hmax, см |
Hкр, м |
H, м |
Периметр сечения, см |
P1.3/ D1.3 |
Pкш/ P1.3 |
Ph / P1.3 |
||
|
P1.3 |
Pкш |
0,5 Ph |
|||||||||
|
1 |
20 |
81 |
70 |
20 |
25 |
85 |
87 |
70 |
4,25 |
1,024 |
1,647 |
|
2 |
20 |
64 |
66 |
15 |
24 |
90 |
95 |
81 |
4,50 |
1,056 |
1,800 |
|
3 |
15 |
60 |
69 |
13 |
19 |
70 |
75 |
90 |
4,67 |
1,071 |
2,571 |
|
4 |
18 |
35 |
50 |
17 |
24 |
70 |
80 |
70 |
3,89 |
1,143 |
2,000 |
|
5 |
20 |
36 |
40 |
19 |
25 |
74 |
79 |
60 |
3,70 |
1,068 |
1,622 |
|
7 |
20 |
40 |
70 |
16 |
20 |
87 |
90 |
57 |
4,35 |
1,034 |
1,310 |
|
8 |
25 |
48 |
80 |
10 |
16 |
75 |
85 |
58 |
3,00 |
1,133 |
1,547 |
|
9 |
20 |
36 |
90 |
12 |
20 |
61 |
71 |
45 |
3,05 |
1,164 |
1,475 |
|
10 |
35 |
40 |
115 |
14 |
25 |
88 |
110 |
70 |
2,51 |
1,250 |
1,591 |
|
11 |
20 |
40 |
120 |
9 |
18 |
56 |
72 |
51 |
2,80 |
1,286 |
1,821 |
|
12 |
24 |
41 |
115 |
8 |
15 |
65 |
67 |
43 |
2,71 |
1,031 |
1,323 |
|
13 |
20 |
35 |
120 |
10 |
20 |
53 |
81 |
51 |
2,65 |
1,528 |
1,925 |
|
14 |
20 |
45 |
117 |
15 |
19 |
62 |
75 |
49 |
3,10 |
1,210 |
1,581 |
|
15 |
27 |
38 |
130 |
10 |
18 |
91 |
110 |
75 |
3,37 |
1,209 |
1,648 |
|
16 |
28 |
45 |
115 |
7 |
15 |
85 |
101 |
67 |
3,04 |
1,188 |
1,576 |
|
17 |
25 |
40 |
120 |
9 |
15 |
69 |
83 |
53 |
2,76 |
1,203 |
1,536 |
|
18 |
25 |
45 |
105 |
8 |
14 |
76 |
98 |
58 |
3,04 |
1,289 |
1,526 |
|
19 |
42 |
40 |
105 |
6 |
16 |
122 |
140 |
94 |
2,90 |
1,148 |
1,541 |
|
20 |
42 |
43 |
107 |
6 |
15 |
114 |
135 |
88 |
2,71 |
1,184 |
1,544 |
|
21 |
25 |
50 |
105 |
8 |
15 |
88 |
100 |
63 |
3,52 |
1,136 |
1,432 |
|
22 |
25 |
51 |
104 |
8 |
16 |
90 |
96 |
56 |
3,60 |
1,067 |
1,244 |
|
23 |
22 |
60 |
100 |
6 |
16 |
77 |
85 |
54 |
3,50 |
1,104 |
1,403 |
|
24 |
20 |
65 |
100 |
7 |
15 |
75 |
76 |
51 |
3,75 |
1,013 |
1,360 |
|
25 |
25 |
71 |
102 |
6 |
16 |
88 |
91 |
61 |
3,52 |
1,034 |
1,386 |
|
26 |
22 |
65 |
103 |
8 |
17 |
75 |
80 |
50 |
3,41 |
1,067 |
1,333 |
|
27 |
25 |
55 |
102 |
8 |
20 |
80 |
90 |
59 |
3,20 |
1,125 |
1,475 |
|
28 |
20 |
70 |
103 |
8 |
20 |
90 |
108 |
64 |
4,50 |
1,200 |
1,422 |
|
29 |
25 |
62 |
105 |
10 |
20 |
75 |
84 |
54 |
3,00 |
1,120 |
1,440 |
|
30 |
25 |
63 |
103 |
9 |
20 |
76 |
81 |
55 |
3,04 |
1,066 |
1,447 |
Примечание. Дерево № 6 исключено из-за резкого отклонения угла местного склона.
Данные идентификации модели (1) представлены в табл. 2. При этом волновыми оказались три закономерности или 300 / 21 = 14,29 %. Их коэффициенты корреляции выделены крупным полужирным шрифтом.
Таблица 2
Факторный анализ влияния параметров берез на отношения между периметрами по детерминированным и волновым биотехническим закономерностям
|
Параметр дерева (влияющий фактор x) |
Относительные параметры комля |
Сумма коэфф. корр. |
Место Ix |
||
|
P1.3/ D1.3 |
Pкш/ P1.3 |
Ph / P1.3 |
|||
|
Угол местного склона j, град |
0,092 |
0,200 |
0,288 |
0,5800 |
7 |
|
Диаметр ствола D1.3, см |
0,661 |
0,134 |
0,8474 |
1,6424 |
4 |
|
Периметр ствола P1.3, см |
0,479 |
0,7380 |
0,7555 |
1,9725 |
2 |
|
Высота комля h, м |
0,576 |
0,517 |
0,335 |
1,4280 |
5 |
|
Макс. высота комля hmax, м |
0,8441 |
0,597 |
0,9110 |
2,3521 |
1 |
|
Высота дерева березы H, м |
0,360 |
0,131 |
0,371 |
0,8620 |
6 |
|
Высота кроны березы Hкр, м |
0,486 |
0,461 |
0,8919 |
1,8389 |
3 |
|
Сумма коэфф. корреляции |
3,4981 |
2,7780 |
4,3998 |
10,6759 |
– |
|
Место Iy |
2 |
3 |
1 |
– |
0,5084 |
С учетом принципа колебательной адаптации деревьев к условиям места своего произрастания на первое место среди параметров деревьев снова встала максимальная высота комля березы. На втором месте оказался периметр на стандартной высоте от корневой шейки, на третьем – высота кроны березы и только на четвертом – диаметр ствола на стандартной высоте. Коэффициент коррелятивной вариации равен 0,5084, из-за волнового влияния максимальной высоты комля, высоты кроны и периметра на высоте 1,3 м на комель, он повысился на 100 (0,5084 – 0,4480) / 0,4480 = 13,48 %.
Относительный сбег комля дерева от сечения на высоте комля до стандартной высоты над корневой шейкой дерева оказался наиболее актуальным для экологической таксации деревьев. Этот показатель наиболее значимый по сравнению с коэффициентом закомелистости, хорошо известным в условиях технологий заготовки кругляка. Это позволит в будущем обратить особое внимание на соотношение периметра в основании комля к периметру ствола дерева на стандартной высоте 1,3 м.
Таким образом, экологическая таксация деревьев коренным образом отличается от технической таксации стволов на древесину в виде кругляка. При этом модель (1) может быть доведена при моделировании по остаткам от предыдущих волновых составляющих даже ниже погрешности измерений.
Далее из табл. 2 выделим закономерности с убывающими значениями коэффициента корреляции, то есть, выполним ранжирование полученных биотехнических закономерностей по ухудшению их адекватности. В табл/ 3 оставлены только сильные связи, то есть закономерности с коэффициентами корреляции свыше 0,7. В итоге доля сильных факторных связей оказалось равной 100×6 / 21 = 28,57 .
Таблица 3
Сильные факторные связи влияния параметров берез
|
Параметр дерева (влияющий фактор x) |
Относительные параметры комля |
||
|
P1.3/ D1.3 |
Pкш/ P1.3 |
Ph / P1.3 |
|
|
Диаметр ствола D1.3, см |
0,8474 |
||
|
Периметр ствола P1.3, см |
0,7380 |
0,7555 |
|
|
Максимальная высота комля hmax, м |
0,8441 |
0,9110 |
|
|
Высота кроны березы Hкр, м |
0,8919 |
||
Из семи параметров деревьев березы три (угол местного склона, высота комля, высота дерева) выпадают при уровне адекватности с коэффициентом корреляции выше 0,7.
В итоге остаются только шесть закономерностей по четырем параметрам комля и кроны дерева, которые приведем полностью в табл. 4 по убыванию их адекватности.
Высокий уровень адекватности отношений между периметрами комля позволяет провести равнение влияния параметров ствола дерева на стандартной высоте 1,3 м (табл. 5).
Коэффициент коррелятивной вариации для всего множества влияния из двух влияющих переменных на четыре показателя равен 3,866 / 8 = 0,4833.
По сравнению со стандартным диаметром коэффициент формы становится намного лучшим влияющим параметром. Среди показателей первое место снова занимает максимальная высота комля.
В табл. 6 даны результаты анализа коэффициентов корреляций с учетом дополнительных волновых составляющих.
Таблица 4
Параметры общего уравнения (2) для сильных факторных связей
|
Номер i |
Вейвлет-сигнал |
|||||||
|
амплитуда колебания |
полупериод колебания |
сдвиг |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
|
|
Максимальная высота комля hmax на Ph / P1.3 с коэффициентом корреляции 0,9110 |
||||||||
|
1 |
1,80620 |
0 |
-8,58792e-5 |
1 |
0 |
0 |
0 |
0 |
|
2 |
-9,75672e-54 |
34,73983 |
0,35371 |
1 |
0 |
0 |
0 |
0 |
|
3 |
8,84959e-89 |
71,27566 |
1,42023 |
1 |
1,29813 |
0,0038235 |
1 |
0,22545 |
|
Высота кроны березы Hкр на Ph / P1.3 с коэффициентом корреляции 0,8919 |
||||||||
|
1 |
8,91974 |
0 |
-5,48964e-5 |
6,46312 |
0 |
0 |
0 |
0 |
|
2 |
-1,71990e-6 |
0 |
-8,17729 |
0,43973 |
0,93745 |
-0,048925 |
0,98417 |
-5,01177 |
|
3 |
1,49204e+8 |
0 |
13,83528 |
0,23748 |
0,99620 |
-0,11600 |
1,10929 |
-1,36516 |
|
Диаметр ствола D1.3 на показатель Ph / P1.3 с коэффициентом корреляции 0,8474 |
||||||||
|
1 |
9,06978 |
0 |
0,0037334 |
1,58273 |
0 |
0 |
0 |
0 |
|
2 |
-0,0073842 |
3,43853 |
0,19645 |
1 |
0 |
0 |
0 |
0 |
|
Максимальная высота комля hmax на P1.3/ D1.3 с коэффициентом корреляции 0,8441 |
||||||||
|
1 |
4,35037 |
0 |
5,40734е-6 |
2,35407 |
0 |
0 |
0 |
0 |
|
2 |
5,55645е-6 |
4,04396 |
0,13465 |
0,86930 |
25,90229 |
-0,088358 |
0,91596 |
2,90565 |
|
Периметр ствола P1.3 на Ph / P1.3 с коэффициентом корреляции 0,7555 |
||||||||
|
1 |
940,9350 |
0 |
5,44516 |
0,036023 |
0 |
0 |
0 |
0 |
|
2 |
3,28134е-60 |
39,75030 |
0,18160 |
1,22261 |
19,83704 |
-0,14275 |
0,95509 |
0,60761 |
|
Периметр ствола P1.3 на Pкш/ P1.3 с коэффициентом корреляции 0,7380 |
||||||||
|
1 |
22,73593 |
0 |
0,017521 |
0,99998 |
0 |
0 |
0 |
0 |
|
2 |
-0,39722 |
1,24880 |
0,038078 |
0,99998 |
0 |
0 |
0 |
0 |
Таблица 5
Факторный анализ влияния параметров сечения на стандартной высоте 1,3 м по детерминированным биотехническим закономерностям
|
Параметр дерева (влияющий фактор x) |
Параметры комля и дерева |
Сумма коэфф. корр. |
Место Ix |
|||
|
H, м |
Hкр, м |
h, см |
hmax, см |
|||
|
Диаметр ствола D1.3, см |
0,238 |
0,501 |
0,356 |
0,580 |
1,675 |
2 |
|
Коэффициент формы P1.3/ D1.3 |
0,573 |
0,439 |
0,526 |
0,653 |
2,191 |
1 |
|
Сумма коэффициента корреляции |
0,811 |
0,940 |
0,882 |
1,233 |
3,866 |
– |
|
Место Iy параметров модели |
4 |
2 |
3 |
1 |
– |
0,4833 |
Таблица 6
Факторный анализ влияния параметров сечения на стандартной высоте 1,3 м по детерминированным и волновым биотехническим закономерностям
|
Параметр дерева (влияющий фактор x) |
Параметры комля и дерева |
Сумма коэфф. корр. |
Место Ix |
|||
|
H, м |
Hкр, м |
h, см |
hmax, см |
|||
|
Диаметр ствола D1.3, см |
0,8400 |
0,681 |
0,356 |
0,580 |
2,457 |
2 |
|
Коэффициент формы P1.3/ D1.3 |
0,8920 |
0,7738 |
0,9097 |
0,9301 |
3,5056 |
1 |
|
Сумма коэффициента корреляции |
1,732 |
1,4548 |
1,2657 |
1,5101 |
5,9626 |
– |
|
Место Iy параметров модели |
1 |
3 |
4 |
2 |
– |
0,7453 |
Учет колебательной адаптации деревьев (рис. 1-5) к условиям места произрастания позволил выйти на первое место полной высоте дерева березы. На втором месте оказалась максимальная высота комля дерева.
Коэффициент коррелятивной вариации стал равным 0,7453, из-за волнового влияния диаметра ствола и коэффициента формы сечения ствола на стандартной высоте, и повысился на
100(0,7453 – 0,4833) / 0,4833 = 54,21 %.
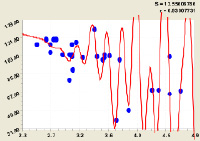
Рис. 1. Влияние коэффициента формы P1.3/ D1.3 на максимальную высоту комля hmax
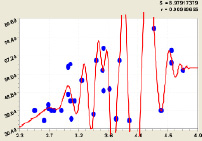
Рис. 2. График влияния коэффициента формы P1.3/ D1.3 на высоту комля h
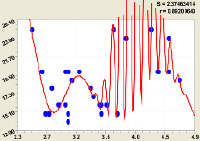
Рис. 3. Влияние коэффициента формы P1.3/ D1.3 на высоту дерева березы H
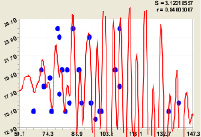
Рис. 4. График влияния диаметра ствола D1.3 на высоту дерева березы H
Из табл. 6 выделим закономерности с убывающим коэффициентом корреляции, то есть по ухудшению их адекватности. В табл. 7 оставлены только сильные связи. Доля сильных факторных связей стало 100⋅5 / 8 = 68,50 %.
Таблица 7
Сильные факторные связи параметров сечения на стандартной высоте 1,3 м по детерминированным и волновым биотехническим закономерностям
|
Параметр дерева (влияющий фактор x) |
Параметры комля и дерева |
|||
|
H, м |
Hкр, м |
h, см |
hmax, см |
|
|
Диаметр ствола D1.3, см |
0,8400 |
|||
|
Коэффициент формы P1.3/ D1.3 |
0,8920 |
0,7738 |
0,9097 |
0,9301 |
На первом месте находится закономерность hmax =f( P1.3/ D1.3), а на втором функция h = f( P1.3/ D1.3). Таким образом, коэффициент формы поперечного сечения ствола на стандартной высоте 1,3 м оказывает решающее влияние на максимальную высоту комля (при условии j>0) и затем на высоту комля берез (при условии j=0).
На третьем рейтинговом месте коэффициент формы оказывает влияние и на формирование всей надземной части дерева по общей высоте.
При уровне адекватности с коэффициентом корреляции выше 0,7 в табл. 7 остаются оба влияющих параметра дерева, но диаметр на стандартной высоте влияет только на полную высоту дерева. В итоге из восьми закономерностей остаются пять, которые приведены полностью в табл. 8 по убыванию адекватности.
Таблица 8
Параметры общего уравнения (1) для сильных факторных связей влияния диаметра и коэффициента формы ствола на стандартной высоте 1,3 м
|
Номер i |
Вейвлет-сигнал |
|||||||
|
амплитуда колебания |
полупериод колебания |
сдвиг |
||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
|
|
Коэффициент формы P1.3/ D1.3 на максимальную высоту комля hmax (рис. 1) |
||||||||
|
1 |
167,65755 |
0 |
0,099983 |
1,33047 |
0 |
0 |
0 |
0 |
|
2 |
0,016041 |
67,71901 |
29,27401 |
0,77473 |
0,14232 |
5,02119 |
-2,96388 |
-0,61587 |
|
3 |
20336,907 |
7,42635 |
15.01560 |
0,073602 |
1,39193 |
-0,23902 |
0,88352 |
2,52136 |
|
Коэффициент формы P1.3/ D1.3 на высоту комля h (рис. 2) |
||||||||
|
1 |
2652,8874 |
5.79409 |
6,38210 |
0,44653 |
0 |
0 |
0 |
0 |
|
2 |
4.58053e-87 |
377,86855 |
65,76463 |
1,14395 |
5.21922 |
-0,72290 |
1.21063 |
-0.60166 |
|
3 |
4,21333e-42 |
239,24332 |
51,89650 |
1,08254 |
0,23520 |
-0,0028716 |
1,82198 |
-3,57386 |
|
4 |
5,74275e-12 |
111,75668 |
30,59882 |
1,03153 |
0,87614 |
0,17356 |
1,00746 |
-4,84928 |
|
Коэффициент формы P1.3/ D1.3 на высоту дерева березы H (рис. 3) |
||||||||
|
1 |
24133,357 |
0 |
5,83779 |
0,19680 |
0 |
0 |
0 |
0 |
|
2 |
9,51271e-20 |
109,0689 |
25,99205 |
1,00336 |
0 |
0 |
0 |
0 |
|
3 |
5,45473e+8 |
0 |
17,35481 |
0,076464 |
0,35115 |
0,022079 |
0,52284 |
0,59742 |
|
4 |
-2,07797e-50 |
297,4083 |
73,76188 |
1 |
0,060540 |
0 |
0 |
-0,42147 |
|
Диаметр ствола D1.3 на высоту дерева березы H (рис. 4) |
||||||||
|
1 |
6,93409 |
6,58071 |
9,72882 |
0,23993 |
0 |
0 |
0 |
0 |
|
2 |
6,75341e-20 |
11,97477 |
0,051590 |
1,12965 |
4,64797 |
-0,11216 |
0,39078 |
5,00726 |
|
3 |
4,78876e-92 |
60,41803 |
0,67147 |
1,00034 |
1,85807 |
-0,0025213 |
0,95920 |
-0,21444 |
|
4 |
5,51666e-42 |
23,49744 |
0,0056824 |
1,64940 |
2,03561 |
0 |
0 |
-4,73658 |
|
Коэффициент формы P1.3/ D1.3 на высоту кроны березы Hкр (рис. 5) |
||||||||
|
1 |
8,91974 |
0 |
-5,48964e-5 |
6,46312 |
0 |
0 |
0 |
0 |
|
2 |
-1,71990e-6 |
0 |
-8,17729 |
0,43973 |
0,93745 |
-0,048925 |
0,98417 |
-5,01177 |
|
3 |
1,49204e+8 |
0 |
13,83528 |
0,23748 |
0,99620 |
-0,11600 |
1,10929 |
-1,36516 |
Волновая теория развития и роста деревьев березы вполне доказана.
Это утверждение исходит также и из того, что по четвертой зависимости известная в лесной таксации показательная закономерность влияния диаметра на высоту (так называемая кривая высот) вида
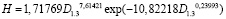 , (2)
, (2)
дает по биотехническому закону коэффициент корреляции всего 0,288.
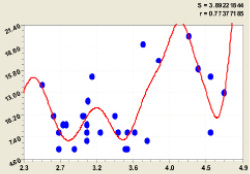
Рис. 5. График влияния коэффициента формы P1.3/ D1.3 на высоту кроны березы Hкр
По детерминированной формуле (2) получается, что для 29 берез, из-за коэффициента корреляции 0,288 меньшем уровня 0,3, по современным представлениям математической статистики факторная связь отсутствует. поэтому таксаторы стараются подбирать пробные площади с высококачественными по форме хвойными деревьями. Измерять сложные формы они не могут.
Дополнением формулы (2) тремя волновыми составляющими колебательного возмущения получена модель вида
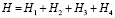 , (3)
, (3)
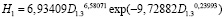 ,
,
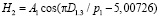 ,
,
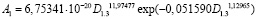 ,
,
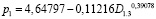 ,
,
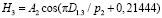 ,
,
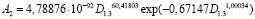 ,
,
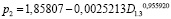 ,
,
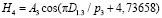 ,
,
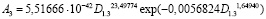 ,
,
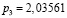 ,
,
у которой коэффициент корреляции достигает 0,8400.
Сравнение показывает, что матричная запись формулы (3) в табл. 8 гораздо компактнее. Но формула (3) нагляднее по отдельным математическим конструктам.
Таким образом, предлагаемое техническое решение основано на результатах фундаментальных исследований влияния параметров деревьев на их относительные показатели по отношениям периметров сечений ствола и комля.
При этом измерения по предлагаемому способу половины сечения комля на полной его высоте просты и наглядны в исполнении.
Кроме того, доказана волновая теория влияния параметров комля на параметры дерева и его кроны. Анализ амплитудно-частотной характеристики (АЧХ) колебательных возмущений формы комля у множества берез из одной популяции растущих учетных деревьев, причем без их разрушения, позволяет проводить по хоуд развития и роста деревьев проводить экологический мониторинга определить закономерности поведения всей популяции.
Поэтому предлагаемый способ может быть применен в индикации не только лесных деревьев, но и фитоиндикации неровных мест произрастания древесных растений, в частности, на склонах оврагов, прирусловых, центральных и притеррасных пойм и берегов водных объектов с березняками.
Библиографическая ссылка
Мазуркин П.М., Алгасова М.А. закономерности относительного сбега комля у множества берез на склоне оврага // Успехи современного естествознания. 2013. № 8. С. 138-145;URL: https://natural-sciences.ru/ru/article/view?id=32749 (дата обращения: 20.02.2026).