Одним из критериев жизнеспособности современного государства является наличие защищенного, динамически развивающегося информационного пространства, пронизывающего все сферы деятельности государства. Защита информации представляет собой комплекс мероприятий, направленных на предотвращение несанкционированной утечки, модификации и удаления информации. Основной задачей обеспечения безопасности информационных компьютерных систем является защита информации и ограничение круга лиц, имеющих доступ к этой критичной информации.
С появлением новых средств мультимедиа и сетей с высокой пропускной способностью, обеспечивающих передачу мультимедийных данных большого объема, в современных вычислительных системах начинают применяться технологии, осуществляющие обработку и передачу больших массивов. Для обеспечения интерактивного обмена данными такие системы должны работать в реальном масштабе времени. Поэтому процедура обеспечения конфиденциальности и целостности информации должна реализоваться с использованием поточных алгоритмов шифрования. Для реализации эффективных методов поточного шифрования данных требуется разработка псевдослучайных последовательностей (ПСП).
Несмотря на то, что шифр, основанный на сложении потока псевдослучайных битов с битами исходного текста по модулю 2 теоретически нераспознаваем, такая система шифрования не отличается стойкостью и может быть раскрыта при наличии определенного количества символов исходного и шифрованного текста. Если известно 2k символов открытого и зашифрованного текста, где k – степень порождающего полинома, то с помощью системы уравнений можно раскрыть структуру генератора ПСП.
Решить данную проблему можно за счет нелинейного шифрования потока данных, которое можно реализовать с использованием операций сложения, умножения и возведения в степень элементов конечного поля, а также их комбинаций [1-4,10].
При реализации нелинейного шифрования псевдослучайная последовательность элементов расширенного поля Галуа получается с помощью регистра сдвига, генерирующего двоичную ПСП. Одновременно с регистра сдвига могут сниматься несколько ПСП элементов поля Галуа {x, y, …}. Данные символы могут сниматься с разных ячеек генератора двоичного ПСП. При этом такая последовательность не будет циклически сдвинутой относительно других псевдослучайных последовательностей элементов.
Рассмотрим нелинейное шифрование потока данных с операцией возведения в степень элемента конечного поля. Данная операция является одной из наиболее употребляемых криптографических процедур. Выбор данной процедуры обусловлен тем, что она нелинейна и для определения исходного текста по символам зашифрованного текста требуется вычисление дискретного логарифма [5-8].
Для шифрования поступающих на вход символов исходного текста, представленного в полиномиальной форме α(z)={αj(z)} вычисляются значения символов псевдослучайной последовательности конечного поля х={xj} на различных текстах работы регистра сдвига j = 0,1,2,… и определяются символы шифрованного сообщения
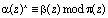 . (1)
. (1)
Для восстановления исходного значения α из получаемого значения β по модулю p используется уравнение вида:
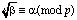 . (2)
. (2)
Однако операция возведения элемента поля в степень трудоемка и требует больших затрат машинного времени. Для сокращения времени выполнения этой процедуры целесообразно перейти к обработке индексов элементов полей Галуа GF(q), где 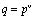 , р – простое число, порожденных неприводимым полиномом π(z). В этом случае операция умножения
, р – простое число, порожденных неприводимым полиномом π(z). В этом случае операция умножения
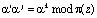 (1)
(1)
можно свести к аддитивной операции
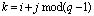 . (2)
. (2)
Операция деления по модулю
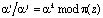 (3)
(3)
может быть представлена в виде
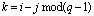 . (4)
. (4)
При этом процедура возведения в степень по модулю
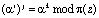 (5)
(5)
представляется к виду
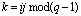 . (6)
. (6)
Операция вычисления дискретного логарифма
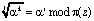 (7)
(7)
сводится к мультипликативной процедуре
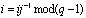 . (8)
. (8)
Анализ данных выражений показывает, что степенное или индексное представления ненулевых элементов удобны для выполнения мультипликативных операций и им обратных. Переход к индексному представлению ненулевых элементов расширенного поля Галуа GF(q) позволяет свести низкоскоростную операцию возведения в степень к операции умножения степеней первообразного элемента α по модулю 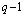 [1-7].
[1-7].
В работах [1, 3, 4] показана структура шифратора для нелинейно шифрования потока данных с операцией возведения в степень элементов открытого текста. Символы исходного текста разбивается на блоки длиной v разрядов и в полиномиальной форме
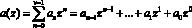 , (9)
, (9)
поступает на вход устройства вычисления индекса по модулю. Данное устройство реализует следующую процедуру
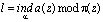 , (10)
, (10)
где a=z; 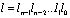 – показатель степени элемента поля.
– показатель степени элемента поля.
Полученное значение показателя степени l подается на первый вход умножителя по модулю 2v–1. На второй вход поступает ключ k (блок двоичных символов длиной v)
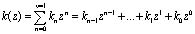 . (11)
. (11)
С выхода устройства снимается результат
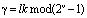 . (12)
. (12)
Данный результат поступает на вход преобразователя «индекс-элемент поля», где реализуется выражение
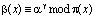 , (13)
, (13)
где b(x) – зашифрованное сообщение.
В результате получается зашифрованное сообщение, которое поступает в канал связи.
Очевидно, что эффективность процедур нелинейного шифрования данных во многом определяется эффективностью алгоритма вычисления индекса элемента поля GF(2v). В работах [6] представлена структура устройства, осуществляющего вычисление индекса элемента поля Галуа по модулю.
Рассмотрим алгоритм расшифрования сообщения с использованием нелинейных операций возведения в степень по модулю. Данный алгоритм приведен в работах [2-5, 9]. Зашифрованное сообщение b(z) (длиной v двоичных разрядов) поступает на вход устройства вычисления индекса элемента поля GF(2v). С выхода данного устройства снимается
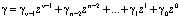 . (14)
. (14)
Для определения значения степени l необходимо операцию деления по модулю свести к мультипликативной операции с обратным элементом
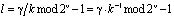 , (15)
, (15)
где 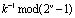 – обратный мультипликативный элемент элементу k по модулю (2v–1).
– обратный мультипликативный элемент элементу k по модулю (2v–1).
Ключ k подается на вход устройства вычисления мультипликативного обратного элемента по модулю (2v–1), с выхода которого снимается значение
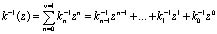 . (16)
. (16)
Значения g и 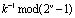 в двоичном коде поступают на вход умножителя по модулю (2v-1), с выхода которого снимается значение
в двоичном коде поступают на вход умножителя по модулю (2v-1), с выхода которого снимается значение
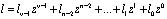 . (17)
. (17)
Данный результат, представляющий собой двоичный блок длиной v разрядов, поступает на вход преобразователя «индекс-элемент поля», где реализуется выражение
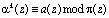 , (18)
, (18)
где 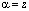 – первообразный элемент поля GF(2v), порождаемый многочленом p(z).
– первообразный элемент поля GF(2v), порождаемый многочленом p(z).
В результате данных преобразований получается открытое сообщение а(z), которое поступает к пользователю. В работах [6-8] показана структура устройства, осуществляющего вычисление элемента поля Галуа по его индексу.
Переход к обработке индексов элементов полей Галуа позволило сократить время выполнения мультипликативных арифметических операций по модулю. Известно, что процедуры выполнения мультипликативных арифметических операций по модулю требуют значительных временных затрат. Так, чтобы вычислить степень mn, где m – элемент некоторого кольца, а n – натуральное число, достаточно выполнить не более 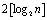 умножений. Тогда
умножений. Тогда
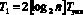 . (19)
. (19)
Комбинационные умножители характеризуются высоким быстродействием, которое определяется лишь задержками сигналов в логических элементах. В этом случае
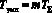 . (20)
. (20)
Сумматор, обладающий минимальной задержкой распространения сигнала, содержит три логических ступени, следовательно, 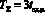 . Тогда
. Тогда
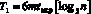 . (21)
. (21)
Рассмотрим процедуру возведения в степень с использованием индексов. Проведя анализ структуры шифратора, приведенных в работах [], можно сделать вывод, что время на выполнение операции нелинейного шифрования определяется
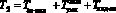 . (22)
. (22)
Время выполнения операции перевода «элемент-индекс» определяется
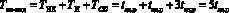 . (23)
. (23)
Время выполнения операции перевода «индекс-элемент» определяется из условия
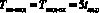 . (24)
. (24)
Положим, что  . Тогда время возведение в степень равно
. Тогда время возведение в степень равно
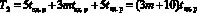 . (25)
. (25)
На рисунке приведена сравнительная характеристика времени выполнения нелинейного шифрования без использования индексного представления (кривая Т1) и с использованием индексов (кривая Т2).
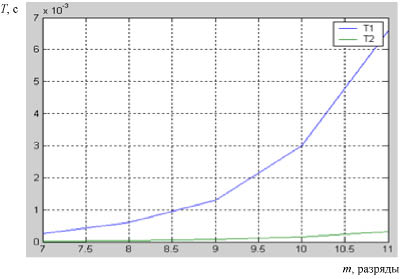
Сравнительная характеристика времени выполнения нелинейного шифрования
Полученные результаты свидетельствуют о том, что применение индексов позволил повысить быстродействие выполнения нелинейного шифрования не мене чем в 2,6 раза. При чем при увеличении разрядности обрабатываемых данных возрастает выигрыш в производительности систем.
Проведенные исследования показали, что применение в нелинейных системах шифрования индексного представления элементов расширенных полей Галуа позволяет реализовать адаптивные средства защиты информации, для которых наличие исходного и шифрованного текста не снижает криптостойкость системы. При этом использование индексирования позволяет обеспечить защиту информации от НСД в интерактивных системах передачи и обработки мультимедийных данных в реальном масштабе времени.
Библиографическая ссылка
Юртаев М.В., Калмыков М.И. ПРИМЕНЕНИЕ НЕЛИНЕЙНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ В СИСТЕМАХ ЗАЩИТЫ ИНФОРМАЦИИ ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА // Успехи современного естествознания. 2014. № 3. С. 131-134;URL: https://natural-sciences.ru/ru/article/view?id=33270 (дата обращения: 04.03.2026).



