Обычно под прогнозированием понимается процесс предсказания будущего основанное на некоторых данных из прошлого, т.е. изучается развитие интересующего явления во времени. Тогда прогнозируемая величина рассматривается как функция времени y=f(t) [1]. Однако в медицине рассматриваются и другие виды прогноза [2]: прогнозируется диагноз, диагностическая ценность нового теста, изменение одного фактора под действием другого и т.д.
Целью статьи было представить различные методы прогнозирования и подходы к их правильному использованию в медицине.
Материалы и методы исследования
В статье рассмотрены следующие методы прогнозирования: методы простой экстраполяции, метод скользящих средних, метод экспоненциального сглаживания, метод среднего абсолютного прироста, метод среднего темпа роста, методы прогнозирования на основе математических моделей.
Результаты исследования и их обсуждение
Как уже было отмечено, прогноз осуществляется на основании некоторой информации из прошлого (базы прогноза). Прежде чем подобрать метод прогнозирования полезно хотя бы качественно оценить динамику изучаемой величины в предыдущие моменты времени. На представленных графиках (рис. 1) видно, что она может быть различной.
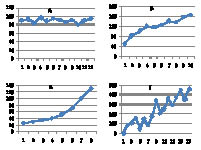
Рис. 1. Примеры динамики изучаемой величины
В первом случае (график А) наблюдается относительная стабильность с небольшими колебаниями вокруг среднего значения. Во втором случае (график Б) динамика носит линейно возрастающий характер, в третьем (график В) – зависимость от времени нелинейная, экспоненциальная. Четвертый случай (график Г)– пример сложных колебаний, имеющих несколько составляющих.
Наиболее распространенным методом краткосрочного прогнозирования (1-3 временных периода), является экстраполяция, которая заключается в продлении предыдущих закономерностей на будущее. Применение экстраполяции в прогнозировании базируется на следующих предпосылках:
• развитие исследуемого явления в целом описывается плавной кривой;
• общая тенденция развития явления в прошлом и настоящем не претерпит серьезных изменений в будущем.
Первый метод из методов простой экстраполяции – это метод среднего уровня ряда. В этом методе прогнозируемый уровень изучаемой величины принимается равным среднему значению уровней ряда этой величины в прошлом. Этот метод используется, если средний уровень не имеет тенденции к изменению, или это изменение незначительно (нет явно выраженного тренда, рис. 1, график А)
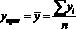 ,
,
где yпрог – прогнозируемый уровень изучаемой величины; yi – значение i-го уровня; n – база прогноза.
В некотором смысле отрезок динамического ряда, охваченный наблюдением, можно уподобить выборке, а значит, полученный прогноз будет выборочным, для которого можно указать доверительный интервал
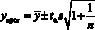 ,
,
где 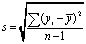 – среднеквадратичное отклонение временного ряда; tα –критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n–1).
– среднеквадратичное отклонение временного ряда; tα –критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n–1).
Пример. В табл. 1 приведены данные временного ряда y(t). Рассчитать прогнозное значение y на момент времени t =13 методом среднего уровня ряда.
Таблица 1
Данные временного ряда y(t)
|
T |
yi |
Прогноз |
|
|
1 |
80 |
||
|
2 |
98 |
||
|
3 |
94 |
(80+98)/2 |
89 |
|
4 |
103 |
(80+98+94)/3 |
90,7 |
|
5 |
84 |
(80+98+94+103)/4 |
93,8 |
|
6 |
115 |
(80+98+94+103+84)/5 |
91,8 |
|
7 |
98 |
(80+98+94+103+84+115)/6 |
95,7 |
|
8 |
113 |
(80+98+94+103+84+115+98)/7 |
96,0 |
|
9 |
114 |
(80+98+94+103+84+115+98+113)/8 |
98,1 |
|
10 |
87 |
(80+98+94+103+84+115+98+113+114)/9 |
99,9 |
|
11 |
107 |
(80+98+94+103+84+115+98+113+114+87)/10 |
98,6 |
|
12 |
85 |
(80+98+94+103+84+115+98+113+114+87+107)/11 |
99,4 |
|
13 |
(80+98+94+103+84+115+98+113+114+87+107+85)/12 |
98,2 |
Исходный и сглаженный ряд представлены на рис. 2, расчет y – в табл. 2.
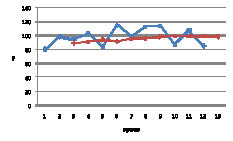
Рис. 2. Исходный и сглаженный ряд
Таблица 2
Доверительный интервал для прогноза в момент t =13
|
yпрог |
n |
t0.05 |
s |
Нижний предел 95ДИ % |
Верхний предел 95ДИ % |
|
98,2 |
12 |
2,2 |
12,4 |
69,7 |
126,7 |
Метод скользящих средних – это метод прогнозирования на краткосрочный период, основан на процедуре сглаживания уровней изучаемой величины (фильтрации). Преимущественно используются линейные фильтры сглаживания с интервалом m, т.е.
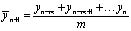 .
.
Доверительный интервал
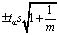
где 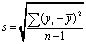 – среднеквадратичное отклонение временного ряда; tα – критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n–1).
– среднеквадратичное отклонение временного ряда; tα – критерий Стъюдента для заданного уровня значимости и числа степеней свободы (n–1).
Пример. В табл. 3 приведены данные временного ряда y(t). Рассчитать прогнозное значение y на момент времени t =13 методом скользящих средних с интервалом сглаживания m=3.
Исходный и сглаженный ряд представлены на рис. 3, расчет y – в табл. 4.
Таблица 3
Данные временного ряда y(t)
|
T |
yi |
прогноз |
|
|
1 |
80 |
||
|
2 |
98 |
||
|
3 |
94 |
||
|
4 |
103 |
(80+98+94)/3 |
90,7 |
|
5 |
84 |
(98+94+103)/3 |
98,3 |
|
6 |
115 |
(94+103+84)/3 |
93,7 |
|
7 |
98 |
(103+84+115)/3 |
100,7 |
|
8 |
113 |
(84+115+98)/3 |
99 |
|
9 |
114 |
(115+98+113)/3 |
108,7 |
|
10 |
87 |
(98+113+114)/3 |
108,3 |
|
11 |
107 |
(113+114+87)/3 |
104,7 |
|
12 |
85 |
(114+87+107)/3 |
102,7 |
|
13 |
прогноз |
(87+107+85)/3 |
93 |
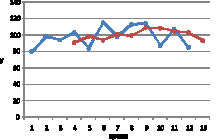
Рис. 3. Исходный и сглаженный ряд
Таблица 4
Прогнозное значение y
|
yпрог |
n |
m |
t0.05 |
s |
Нижний предел 95ДИ % |
Верхний предел 95ДИ % |
|
93 |
12 |
3 |
2,2 |
12,4 |
61,4 |
124,6 |
Метод экспоненциального сглаживания – это метод, при котором в процессе выравнивания каждого уровня используются значения предыдущих уровней, взятых с определенным весом. По мере удаления от какого-то уровня вес этого наблюдения уменьшается. Сглаженное значение уровня на момент времени t определяется по формуле
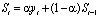
где St – текущее сглаженное значение; yt – текущее значение исходного ряда; St – 1 – предыдущее сглаженное значение; α – сглаживающая параметр.
S0 берется равным среднему арифметическому нескольких первых значений ряда.
Для расчета α предложена следующая формула
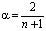 .
.
По поводу выбора α нет единого мнения, эта задача оптимизации модели пока еще не решена. В некоторых литературных источниках рекомендуется выбирать 0,1 ≤ α ≤ 0,3.
Прогноз рассчитывается следующим образом
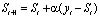 .
.
Доверительный интервал
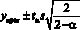 .
.
Пример. Рассчитать прогнозное значение y на момент времени t =11 методом экспоненциального сглаживания (табл. 5). Зададим α=0,3, S0 – среднее значение по трем первым членам ряда.
Таблица 5
Данные временного ряда y(t)
|
t |
yi |
St |
|
|
0 |
(80+98+94)/3 |
90,7 |
|
|
1 |
80 |
0,3×80+(1-0,3)×90,7 |
87,5 |
|
2 |
98 |
0,3×98+(1-0,3) ×87,5 |
90,6 |
|
3 |
94 |
0,3×94+(1-0,3) ×90,6 |
91,6 |
|
4 |
103 |
0,3⋅103+(1-0,3) ×91,6 |
95,0 |
|
5 |
84 |
0,3×84+(1-0,3) ×95 |
91,7 |
|
6 |
115 |
0,3⋅115+(1-0,3) ×91,7 |
98,7 |
|
7 |
98 |
0,3×98+(1-0,3) ×98,7 |
98,5 |
|
8 |
113 |
0,3⋅113+(1-0,3) ×98,5 |
102,8 |
|
9 |
114 |
0,3⋅114+(1-0,3) ⋅102,8 |
106,2 |
|
10 |
87 |
0,3×87+(1-0,3) ⋅106,2 |
100,4 |
|
11 |
107 |
0,3⋅107+(1-0,3) ⋅100,4 |
102,4 |
|
12 |
85 |
0,3×85+(1-0,3) ⋅102,4 |
97,2 |
|
13 |
прогноз |
97,2+0,3× (85-97,2) |
93,5 |
Исходный и сглаженный ряд представлены на рис. 4, расчет y – в табл. 6.
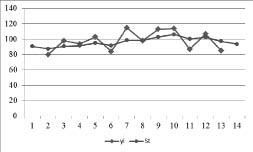
Рис. 4. Исходный и сглаженный ряд
Таблица 6
Прогнозное значение y на момент времени t =11
|
yпрог |
n |
α |
t0.05 |
s |
Нижний предел 95ДИ % |
Верхний предел 95ДИ % |
|
93,5 |
12 |
0,3 |
2,2 |
12,4 |
63,8 |
123,2 |
Следующий метод прогноза – это метод среднего абсолютного прироста Прогнозируемый уровень изучаемой величины изменяется в соответствии со средним абсолютным приростом этой величины в прошлом. Данный метод применяется, если общая тенденция в динамике линейна (для случая, приведенного на рис. 1, график Б)
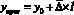 ,
,
где 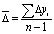 ,
,
где 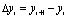 ; y0 – базовый уровень экстраполяции выбирается как среднее значение нескольких последних значений исходного ряда;
; y0 – базовый уровень экстраполяции выбирается как среднее значение нескольких последних значений исходного ряда; 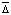 – средний абсолютный прирост уровней ряда; l – число интервалов прогнози рования.
– средний абсолютный прирост уровней ряда; l – число интервалов прогнози рования.
Пример. По данным из табл. 7 рассчитать прогнозное значение на t =13,14,15.
В качестве базового уровня принято усредненное значение последних значений ряда, максимально трех.
Таблица 7
Данные временного ряда y(t)
|
t |
yi |
Δyi= yi+1–yi |
y0 |
Прогноз = y0+Δl |
|
1 |
60 |
|||
|
2 |
75 |
15 |
60 |
68,2 |
|
3 |
70 |
-5 |
(60+75)/2=67,5 |
75,7 |
|
4 |
103 |
33 |
(60+75+70)/3=68,3 |
76,5 |
|
5 |
100 |
-3 |
(75+70+103)/3=82,7 |
90,9 |
|
6 |
115 |
15 |
(70+103+100)/3=91 |
99,2 |
|
7 |
125 |
10 |
(103+100+115)/3=106 |
114,2 |
|
8 |
113 |
-12 |
(100+115+125)/3=113,3 |
121,5 |
|
9 |
138 |
25 |
(115+125+113)/3=117,7 |
125,9 |
|
10 |
136 |
-2 |
(125+113+138)/3=125,3 |
133,5 |
|
11 |
145 |
9 |
(113+138+136)/3=129 |
137,2 |
|
12 |
150 |
5 |
(138+136+145)/3=139,7 |
147,9 |
|
13 |
(136+145+150)/3=143,7 |
143,7+8,2⋅1=151,9 |
||
|
14 |
143,7+8,2⋅2=160,1 |
|||
|
15 |
143,7+8,2⋅3=168,3 |
|||
|
|
Исходный и сглаженный ряд представлены на рис. 5.
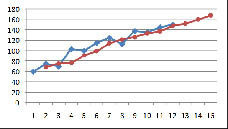
Рис. 5. Исходный и сглаженный ряд
Метод среднего темпа роста
Прогнозируемый уровень изучаемой величины изменяется в соответствии со средним темпом роста данной величины в прошлом. Данный метод применяется, если общая тенденция в динамике характеризуется показательной или экспоненциальной кривой (рис. 1В)
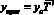 ,
,
где 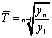 – средний темп роста в прошлом; l – число интервалов прогнозирования.
– средний темп роста в прошлом; l – число интервалов прогнозирования.
Прогнозная оценка будет зависеть от того, в какую сторону от основной тенденции (тренда) отклоняется базовый уровень y0, поэтому рекомендуется рассчитывать y0 как усредненное значение нескольких последних значений ряда.
Пример. По данным из табл. 8 рассчитать прогнозное значение на t=13,14,15.
Таблица 8
Данные временного ряда y(t)
|
t |
yi |
y0 |
|
Прогноз
|
|
1 |
60 |
|||
|
2 |
65 |
|||
|
3 |
70 |
(60+65)/3=62,5 |
(65/60)1 =1,08 |
62,5⋅1,081 = 67,7 |
|
4 |
68 |
(60+65+70)/3=65 |
(70/60)1/2 =1,08 |
65⋅1,081 = 70,2 |
|
5 |
82 |
(65+70+68)/3=67,7 |
(68/60)1/3 =1,04 |
67,7⋅1,041 =70,5 |
|
6 |
80 |
(70+68+82)/3=73,3 |
(82/60)1/4 =1,08 |
73,3⋅1,081 =79,3 |
|
7 |
95 |
(68+82+80)/3=76,7 |
(80/60)1/5 =1,06 |
76,7⋅1,061 =81,2 |
|
8 |
113 |
(82+80+95)/3=85,7 |
(95/60)1/6 =1,08 |
85,7⋅1,081 =92,5 |
|
9 |
135 |
(80+95+113)/3=96 |
(113/60)1/7 =1,09 |
96⋅1,091 =105,1 |
|
10 |
140 |
(95+113+135)/3=114,3 |
(135/60)1/8 =1,11 |
114,3⋅1,111 =126,5 |
|
11 |
168 |
(113+135+140)/3=129,3 |
(140/60)1/9 =1,10 |
129,3⋅1,11 =142,1 |
|
12 |
205 |
(135+140+168)/3=147,7 |
(168/60)1/10 =1,11 |
147,7⋅1,111 =163,7 |
|
13 |
(140+168205)/3=171 |
(205/60)1/11 =1,12 |
171⋅1,121 =191,2 |
|
|
14 |
171⋅1,122 =213,8 |
|||
|
15 |
171⋅1,123 =239,1 |
Исходный и сглаженный ряд представлены на рис. 6.
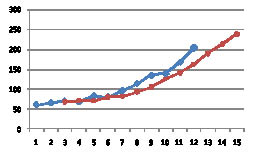
Рис. 6. Исходный и сглаженный ряд
На сегодняшний день наиболее распространенным методом прогнозирования является нахождение аналитического выражения (уравнения) тренда [3]. Тренд экстраполируемого явления – это основная тенденция временного ряда, в некоторой мере свободная от случайных воздействий.
Разработка прогноза заключается в определении вида экстраполирующей функции y=f(t), которая выражает зависимость изучаемой величины от времени на основе исходных наблюдаемых данных. Первым этапом является выбор оптимального вида функции, дающей наилучшее описание тренда. Наиболее часто используются следующие зависимости:
• линейная 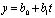 ;
;
• параболическая  ;
;
• показательная функция 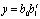 ;
;
Проблемы нахождения коэффициентов линейной функции и прогноз на ее основе рассматриваются в разделе статистики «регрессионный анализ». Если форма кривой, описывающей тренд, имеет нелинейный характер, то задача оценки функции y=f(t) усложняется, и в этом случае необходимо привлечь к анализу специалистов по биостатистике и воспользоваться компьютерными программами по статистической обработке данных.
В большинстве реальных случаев временной ряд представляет собой сложную кривую, которую можно представить как сумму или произведение трендовой, сезонной, циклической и случайной компонент.
Тренд представляет собой плавное изменение процесса во времени и обусловлен действием долговременных факторов. Сезонный эффект связан с наличием факторов, действующих с заранее известной периодичностью (например, времена года, лунные циклы). Циклическая компонента описывает длительные периоды относительного подъема и спада, состоит из циклов переменной длительности и амплитуды (например, некоторые эпидемии имеют длительный циклический характер). Случайная составляющая ряда отражает воздействие многочисленных факторов случайного характера и может иметь разнообразную структуру.
Заключение
Методы простой экстраполяции, метод скользящих средних, метод экспоненциального сглаживания являются простейшими, и в тоже время самыми приближенными – это видно из широких доверительных интервалов в приведенных примерах. Большая погрешность прогноза наблюдается в случае сильных колебаний уровней. Следует обратить внимание на то, что неправомерно использовать эти методы при наличии явной тенденции к росту (или падению) исходного временного ряда. Тем не менее, для краткосрочных прогнозов их применение бывает оправданным.
Анализ всех компонентов временного ряда и прогнозирование на их основе задача нетривиальная, рассматривается в разделе статистики «анализ временных рядов» и требует специальной подготовки.
Библиографическая ссылка
Койчубеков Б.К., Сорокина М.А., Мхитарян К.Э. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ В МЕДИЦИНЕ // Успехи современного естествознания. 2014. № 4. С. 29-36;URL: https://natural-sciences.ru/ru/article/view?id=33316 (дата обращения: 26.12.2025).




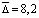
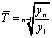
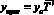 ,
,