Гиперкомплексные числа находят применение в различных областях геометрии и физики. Задание гиперкомплексной числовой системы всегда производится с помощью так называемой «таблицы умножения» базисных элементов. Бинарная алгебраическая операция описывается с помощью символьной таблицы, а ведь в то же время для унарных алгебраических операций давно и очень продуктивно используется матричный аппарат. Для задания линейного оторбажения линейного пространства образы n базисных векторов, а именно векторы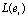 
, записывают в виде столбцов матрицы этого линейного отображения (оператора). Матрицы традиционно являются объектами, используемыми для задания линейных операторов. Очевидно, что для задания билинейной операции квадратная двумерная матрица недостаточна, так как требуется задать образы всех произведений элементов базиса, а именно n2 всевозможных произведений 
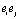пар элементов базиса. Таким образом, для задания конечномерной алгебры требуется n3 элементов, то есть n2 векторов. Получающаяся матрица на одну размерность больше, то есть трёхмерная, содержит n2 векторов, получающихся в результате умножений базисных векторов eiej, где i, j=1,…,n.
Подробнее покажем, как строится трёхмерная матрица для системы комплексных чисел. Если обозначить 1,i как обычные базисные векторы в плоскости, то есть e1, e2, то для равенства i2= –1 запись будет в виде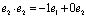 
, аналогично 
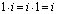соответствует 
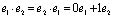, а 
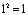означает 
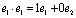. В итоге из восьми координат четырёх получившихся векторов, для задания системы комплексных чисел получилась бы такая трёхмерная матрица из 8 чисел, которые называются «структурными константами» системы:
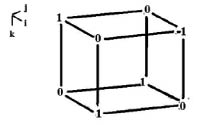
Рис. 1
В одном сечении вдоль вертикального направления присутствует матрица
,
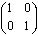соответствующая умножению на единицу, в плоскости это соответствует тождественному линейному оператору. Во втором сечении матрица
,
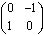соответствующая умножению на мнимую единицу, в плоскости это соответствует линейному оператору поворота на 90°.
Вертикальные сечения соответствуют матрицам тех или иных линейных операторов, задающих умножение на один из элементов системы.
Линейная комбинация вертикальных сечений с коэффициентами A,B соответствует линейному оператору умножения на число A+Bi.
Каждая отдельная координата образа может быть задана как билинейная форма от пары исходных векторов, так, для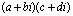 
первая координата 
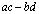, соответственно, в верхнем горизонтальном сечении содержится матрица
,
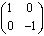которая задаёт преобразование пары векторов в одно число так:
.
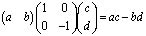Вторая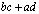 
, соответственно в нижнем сечении матрица
,
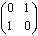соответственно
.
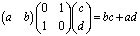Матричный способ задания гиперкомплексных числовых систем был предложен автором данной статьи в 1990-е годы, тогда же был доложен на семинарах кафедры алгебры Томского государственного университета, а в 2004 г. опубликованы статьи [3, 4], где рассматривался и применялся данный способ задания гиперкомплексных систем, а также систем с n-арными алгебраическими операциями. Матричный способ задания гиперкомплексных систем пока не получил широкого применения: так, на международном математическом сайте wolfram.com умножение мнимых единиц до сих пор задаётся с помощью символьной таблицы умножения либо просто через системы равенств.
Кватернионы – это 4-мерная система с одной действительной единицей и тремя мнимыми единицами: i, j, k. Умножение в данной системе задано так:
, 
,
, 
.
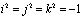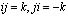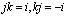Таким образом, так называемая «таблица умножения» имеет вид:
Рис. 2
Таким же образом может быть построена матрица, задающая систему кватернионов. Эта матрица содержит не символьную информацию, а числа:
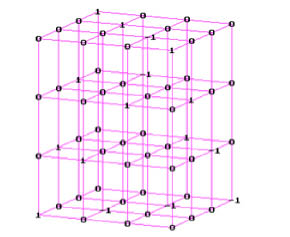
Рис. 3
Векторное умножение в трёхмерном пространстве также может быть задано матрицей. Примечание. В теории пространственных матриц [1] третий индекс исторически было принято увеличивать снизу вверх, что и сделано для рассмотренных матриц.
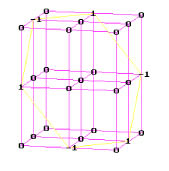
Рис. 4
Общий аппарат описания алгебраических структур с помощью многомерных матриц может помочь более глубокому пониманию взаимосвязи между линейными операторами (унарными операциями), бинарными и произвольными алгебраическими операциями. В [5] показано, каким образом понимание теоретических основ математики способствует лучшему восприятию методов решения практических задач. Несомненно, гиперкомплексные числовые системы необходимо изучать в курсе алгебры с помощью матричного аппарата, с рассмотрением строения пространственных матриц и их сечений. Единообразие способа задания алгебраических операций с помощью матриц позволяет легко переходить к изучению n-арных операций [4].
Библиографическая ссылка
Приходовский М.А. ГИПЕРКОМПЛЕКСНЫЕ ЧИСЛОВЫЕ СИСТЕМЫ И ПРОСТРАНСТВЕННЫЕ МАТРИЦЫ // Успехи современного естествознания. – 2014. – № 4. – С. 79-81;URL: https://natural-sciences.ru/ru/article/view?id=33328 (дата обращения: 23.11.2024).