Проблемы охраны и управления качеством окружающей среды порождают широкий класс задач, связанных с поиском оптимальных решений при подготовке народнохозяйственных проектов, осуществление которых сопряжено с воздействием на природную среду, а также с планированием природоохранных мероприятий, требующих управления выбросами действующих промышленных объектов с учетом особенностей гидрометеорологического режима и ограничений санитарного и социально-экономического характера.
В связи с этим в практике хозяйствования все большее значение приобретают методы улучшения качества окружающей среды. К этим методам можно отнести:
- реконструкцию и усовершенствование действующих технологических линий, обеспечивающих снижение выбросов примесей и вредных отходов;
- разработку и внедрение малоотходных (замкнутых) технологических процессов, обеспечивающих комплексное использование всех компонентов и минимальное поступление выбросов в окружающую среду.
Выбор методов управлений, наиболее эффективных с точки зрения «природоохранных» и «производственных» критериев, является непростой задачей, решение которой вряд ли возможно без применения метода экономико-эколого-математического моделирования на ЭВМ.
В настоящее время в связи с увеличением возможностей компьютерного обеспечения метод математического моделирования экологических процессов является одним из наиболее перспективных, позволяющих учитывать особенности технической нагрузки на окружающую среду, рассматривать остроту экологической ситуации территории в зависимости от уровня заболеваемости проживающего населения.
Результаты подобного моделирования могут быть использованы при принятии решений в областях экологии, здравоохранения, отраслевой медицины, планирования инвестиций, градостроения и т.д.
Несмотря на отсутствие прямой связи между понятиями «экология» и «инвестиции», они тем не менее являются взаимодополняющими факторами. Предприятиям в настоящее время необходимо осуществлять инвестирование с постоянной оглядкой на экологию.
Общее ухудшение экологической обстановки, необходимость точно прогнозировать и принимать оперативные решения по преодолению последствий загрязнения требуют создания специальных математических моделей, в которых отражается оценка степени загрязнения атмосферы. Успешное решение задач прогноза основано на использовании математических моделей.
На изучаемом предприятии Таразский металлургический завод («ТМЗ») используются традиционные методы контроля, которые базируются на точечном апробировании основных природных компонентов территории: воздушной, водной, почвенной среды и биоты. Анализ полученных данных сопряжен со значительными трудностями, связанными с отсутствием оптимального метода обработки данных. Основные трудности, возникающие при оценке, прогнозе, контроле и других аспектах процесса регулирования уровня загрязнения, связаны с ее высокой динамичностью как во времени, так и в пространстве, что обуславливает необходимость создания эффективных моделей, способов и методов, направленных на их научно-обоснованное решение.
На практике часто за основу расчетов концентраций загрязняющих веществ в атмосфере берут «Методику расчета концентраций загрязняющих веществ в атмосферном воздухе, вредных веществ, содержащихся в выбросах предприятий (ОНД-86)». С момента разработки данной методики прошло более 20 лет, и многие коэффициенты, применяемые в расчетах, устарели. В настоящее время имеются несколько типов моделей, отражающих те или иные аспекты взаимодействия общества и среды с учетом загрязнения окружающей среды и его социально-экономических последствий.
В работах [1-5] сформулирован ряд математических моделей для решения такого рода задач.
В работах изложены исследования общего уровня загрязнения воздушного бассейна г. Тараз, выявлены источники загрязнения и их влияние на уровень заболеваемости населения. Так, значительный урон атмосфере города наносится транспортом, котельными и основными градообразующими предприятиями химической промышленности.
Основными компонентами загрязнения воздушного бассейна производства «ТМЗ» служат углерод оксида, азот оксида, древесная пыль, взвешенные вещества, значительную концентрацию составляют также фенол и формальдегид, метилбензол и оксид азота.
В данной работе мы рассматриваем математическую модель, основанную на численном решении уравнения переноса и диффузии загрязняющих примесей в химической промышленности. В качестве целевой функции выступает функционал стоимости ущерба от отдельных источников и затрат на их оптимизацию. Эти функции зависят от концентрации примесей и могут зависеть от входных параметров модели.
Пусть рассматриваемый регион расположен в ограниченной трехмерной области D = ∑·[О, Н] и на его территории имеется п промышленных предприятий, производящих выбросы вредных веществ в атмосферу.
Мы рассмотрим, модель основанную на понятии функции стоимости регулирования источников [3, 4, 5].
Введем, следуя [8], следующие обозначения: Gm(lm) – функция, характеризующая стоимость уменьшения интенсивности выбросов на т – М предприятий на величину 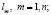
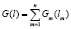 общая стоимость регулирования источников в пределах данного региона.
общая стоимость регулирования источников в пределах данного региона.
Пусть S – стоимость всех средств, используемых для улучшения качества атмосферы. Тогда множество Е можно считать заданным в виде
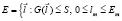 , (1)
, (1)
Для построения зависимостей Gm(lm), т = 1, п имеется несколько путей. Например, когда уменьшение выбросов производится за счет предварительной очистки исходного сырья или топлива, то стоимость регулирования может быть определена как функция от веса элементов, отделенных в результате очистки. Гораздо сложнее обстоит дело, когда для уменьшения выбросов используются такие методы, как модернизация и реконструкция существующего производства. В этом случае затраты на эти мероприятия могут дать одновременно и положительный производственный эффект. Даже такая сугубо атмосфероохранная мера, как повышение высоты трубы, увеличивает интенсивность процесса горения, что повышает эффективность производства за счет более полной утилизации сырья и топлива [1, 6].
Следуя [8], будем понимать под стоимостью противозагрязняющих мероприятий на предприятии (Gm(lm)) сумму всех издержек, которые несет данное предприятие, при уменьшении объема вредных выбросов на величину ет, т = 1, п и неизменном объеме выпускаемой продукции. Основные статьи этих издержек связаны с закупкой других, более дорогих видов сырья и материалов, дополнительными капиталовложениями и эксплуатационными затратами на основания новых малоотходных технологий, увеличением себестоимости производимой продукции и, следовательно, уменьшением прибыли от ее реализации.
Для расчета этих элементов составляющих, стоимость предотвращения загрязнения, может быть успешно применен метод экономико-математического моделирования [3,4].
Рассмотрим далее метод построения функций Gm(lm, основанный на использовании одной из простейших и наиболее употребительных моделей- линейной производственной модели [188,189]. Будем исходить прежде всего из того, что рассматриваемой производственной единице (m-му предприятию) установлено плановое задание по выпуску Jm видов продукции в объемах за время Т. Для выполнения этого задания предприятие располагает технологическими способами (rm).
Обозначим через hm1 интенсивность использования 1-й технологии на предприятии, т – М, l = 1, rm; hm ={hm1, hm2, hmk) – вектор интенсивного (план) функционирования m – го предприятия. Представим экономико-математическую модель работы данного предприятия следующим образом:
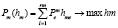 (прибыль), (2)
(прибыль), (2)
При ограничениях:
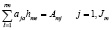 (плановое задание), (3)
(плановое задание), (3)
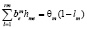 (предельно допустимые выбросы), (4)
(предельно допустимые выбросы), (4)
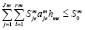 (себестоимость), (5)
(себестоимость), (5)
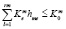 (капиталовложения), (6)
(капиталовложения), (6)
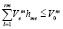 (эксплуатационные затраты). (7)
(эксплуатационные затраты). (7)
Здесь используются следующие обозначения:
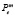 – прибыль т-го предприятия при использовании е- й технологии с единичной мощностью;
– прибыль т-го предприятия при использовании е- й технологии с единичной мощностью;
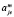 – объем выпуска продукции вида j на m-м предприятии по способу производства;
– объем выпуска продукции вида j на m-м предприятии по способу производства; 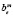 – мощность выброса примеси на m-м предприятии по е-й технологии с единичной мощностью;
– мощность выброса примеси на m-м предприятии по е-й технологии с единичной мощностью; 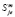 – себестоимость производства единицы продукции е-го вида для m-го предприятия по технологическому способу;
– себестоимость производства единицы продукции е-го вида для m-го предприятия по технологическому способу; 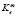 – капитальные вложения на предотвращение загрязнения атмосферы в е-ю технологию на m-м предприятии (
– капитальные вложения на предотвращение загрязнения атмосферы в е-ю технологию на m-м предприятии (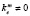 для вновь осваиваемых и реконструируемых технологий);
для вновь осваиваемых и реконструируемых технологий); 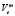 – затраты на эксплуатацию и содержание газоочистных установок и других очистных сооружений в связи с применением е-го технологического способа на m-м предприятии;
– затраты на эксплуатацию и содержание газоочистных установок и других очистных сооружений в связи с применением е-го технологического способа на m-м предприятии; 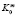 – лимит капиталовложений для е-го предприятия;
– лимит капиталовложений для е-го предприятия; 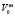 – лимит эксплуатационных затрат на m-м предприятии;
– лимит эксплуатационных затрат на m-м предприятии; 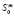 – предельная величина себестоимости выпускаемой т-м предприятием продукции.
– предельная величина себестоимости выпускаемой т-м предприятием продукции.
Оптимальный план функционирования т-го предприятия определяется с помощью решения задачи линейного программирования (5.17) – (5.22). Переменная ет участвует в этой задаче как параметр. Величина Ет в рамках принятой модели может быть определена из решения задачи линейного программирования:
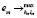
при ограничениях (5.12)-(5.17). Если 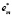 – оптимальное решение этой задачи, то
– оптимальное решение этой задачи, то 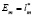 .
.
Пусть 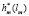 – вектор оптимального решения задачи оптимизации (2) – (7), зависящий от параметра. Используя введенные обозначения, вычислим следующие величины:
– вектор оптимального решения задачи оптимизации (2) – (7), зависящий от параметра. Используя введенные обозначения, вычислим следующие величины:
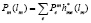 – прибыль m-го предприятия при оптимальном плане
– прибыль m-го предприятия при оптимальном плане 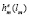 ;
;
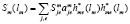 – себестоимость продукции на т-м предприятии при оптимальном плане
– себестоимость продукции на т-м предприятии при оптимальном плане 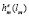
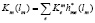 – объем капиталовложений на оздоровление атмосферы, требуемый m-му предприятию при данном режиме работы;
– объем капиталовложений на оздоровление атмосферы, требуемый m-му предприятию при данном режиме работы;
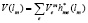 – стоимость всех эксплуатационных затрат, связанных с работой очистных сооружений и установок при плане работы m-го предприятия.
– стоимость всех эксплуатационных затрат, связанных с работой очистных сооружений и установок при плане работы m-го предприятия.
Определим суммарные издержки m-го предприятия (функцию 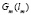 ), возникающие вследствие уменьшения выбросов на lm. Тогда
), возникающие вследствие уменьшения выбросов на lm. Тогда
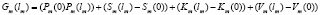 . (8)
. (8)
Отметим, что 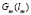 как функция lm является кусочно-линейной функцией на [0, Ет]. Это следует из общего свойства решения задач линейного программирования, – вектор-функция
как функция lm является кусочно-линейной функцией на [0, Ет]. Это следует из общего свойства решения задач линейного программирования, – вектор-функция 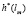 «склеена» из кусков линейных отрезков в Rm. Поэтому для построения функции стоимости Gm(lm) достаточно иметь решения нескольких задач линейного программирования вида (5.17) – (5.22), которые последовательно принимают значения, равные точкам излома графика вектор – функции
«склеена» из кусков линейных отрезков в Rm. Поэтому для построения функции стоимости Gm(lm) достаточно иметь решения нескольких задач линейного программирования вида (5.17) – (5.22), которые последовательно принимают значения, равные точкам излома графика вектор – функции 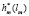 .
.
Город Тараз является типичным представителем городов Казахстана с населением около 400 тыс. человек, с экологическими проблемами, свойственными для районных городов с умеренным промышленным потенциалом.
Безусловно, разработка моделей атмосферной диффузии в их связи с предельным уровнем заболеваемости, используемых для решения широкого круга прикладных задач, в том числе связанных с подготовкой природоохранных мероприятий, оценкой риска для здоровья населения и др., имеет большое научное и практическое значение.
Анализ результатов моделирования показывает, что при регламентном решении работы предприятия и одновременно работающих источников выбросов экологические характеристики атмосферного воздуха в районе расположения ТМЗ лишь по некоторым загрязняющим компонентам находятся в пределах нормативных величин, а в целом происходит значительное влияние на изменение уровня загрязнения атмосферы города и на здоровье населения.
Таким образом, построенная экономико-математическая модель управления используется для описания процессов распространения загрязнителей в численных моделях. Это позволяет получить оценку уровней загрязнения в точках рассматриваемого региона, которые далее могут быть использованы для формирования критерия качества воздушного бассейна области. Целевая функция представлена в виде свертки кусочно-линейной функции.
Библиографическая ссылка
Абдула Ж., Галагузова Т.А., Омарова А.Ж. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЗАГРЯЗНЕНИЯ АТМОСФЕРЫ ХИМИЧЕСКОЙ ПРОМЫШЛЕННОСТИ // Успехи современного естествознания. 2014. № 5-1. С. 202-205;URL: https://natural-sciences.ru/ru/article/view?id=33891 (дата обращения: 02.01.2026).



