Последовательности многомерных точек, могут обладать различными свойствами равномерности [1].Сложность заключается в том, что для решения практических задач эти свойства должны выполняться уже при сравнительно небольших количествах точек. Только в этом случае данные последовательности могут быть успешно использованы при решении практических задач,относящихся к теории кубатурных формул, в задачах оптимизации, и т.д. С этой целью в [2] были сформулированы некоторые дополнительные требования к равномерно распределенным последовательностям, а также новые условия [1], обеспечивающие, как это показано в данной работе, существование ЛПτ-последовательностей.
Свойство А. Рассмотрим Кn – единичный n-мерный куб. Разобьем Кn плоскостями
хj = I/2 при j=I, 2, …n на t =2n октантов, которые будем считать двоичными параллелепипедами. Разобьем последовательность точек PI, I=1,… на двоичные участки, длина которых равна 2n: Р0, Рt-1,Pt, …, Р2t-1, Р2t, …, P3t-1, … . Если в любом из этих участков все точки принадлежат различным октантам, то мы говорим, что последовательность обладает свойством А.
Согласно [2] справедлива теорема: ЛПτ-последовательность Р0, Р1, …, PI, … обладает свойством А тогда и только тогда, когда определитель (размером n x n), составленный из первых столбцов всех направляющих матриц, равен I (mod 2).Данная теорема дает возможность строить ЛПτ-последовательности со свойством А. Однако остается открытым вопрос: можно ли в качестве последовательности моноциклических операторов {Lk} [1], по которым рассчитываются значения соответствующих координат точек ЛПτ последовательности, брать все операторы низших порядков. Вопрос обоснован тем, что именно в этом случае значение t будет минимальным, что наилучшим образом отразится на всех характеристиках равномерности. Для ответа на него рассмотрим следующие утверждения.
Пусть L1 , L2 , …, Ln – различные моноциклические операторы с порядками
m1, m2, …, mn соответственно.
Лемма 1. Пусть рj(I) – есть ДР – последовательности [1], соответствующие всем моноциклическим операторам низших порядков L1, … Ln. Пусть m - порядок оператора Ln. Тогда справедливо следующее неравенство:
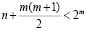 при m≥5 (1.1)
при m≥5 (1.1)
Доказательство. Доказательство проведем индукцией по m. При m=5 неравенство справедливо, т.к. максимальное n при этом равно 13 [2]. Пусть для некоторого m имеет место (1.1) при любом n, соответствующем данному m. Докажем, что при любом n, соответствующем m+I, будет выполняться аналогичное неравенство. Учитывая, что число моноциклических операторов порядка m+I равно 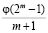 , (где j(k) – теоретико-числовая функция Эйлера, равная количеству натуральных чисел меньших k и взаимно простых с k) докажем, что
, (где j(k) – теоретико-числовая функция Эйлера, равная количеству натуральных чисел меньших k и взаимно простых с k) докажем, что
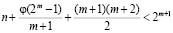 .
.
Преобразуем данное неравенство следующим образом :
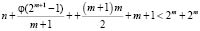 .
.
Сравнивая его с (1.1), остается показать, что
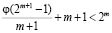 ,
,
т.е. 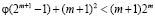 . Очевидно, что
. Очевидно, что
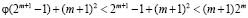 .
.
Окончательно имеем
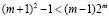 ,
,
т.е. приходим к очевидному неравенству, которое справедливо при m≥3.
Пусть m(n) – порядок моноциклического оператора, стоящего на n-м месте в последовательности всех моноциклических операторов, взятых подряд.
Лемма 2. Рассмотрим n-I последовательность элементов GF(2) {uI(k)}, k=1,…, n–1, I=0,1,2,… Пусть к данному набору принадлежит последовательность, состоящая из единиц, и пусть определитель
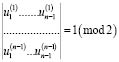 .
.
Рассмотрим моноциклический оператор Ln порядка m≥ m(n), m≥5. Тогда существует такое решение оператора Ln – {uI(n)}, что определитель
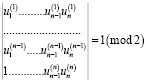 (1.2)
(1.2)
Доказательство. Допустим обратное: как-бы ни выбирать первые m значений решения оператора Ln определитель (1.2) равен 0 (mod 2). Т.к. столбцы предыдущего определителя линейно независимы, то первые n–I элементы последнего столбца в (1.2) единственным образом выразятся через эти столбцы. Но в силу указанного предположения, последний элемент n-го столбца в (1.2) должен таким же образом выражаться через элементы n-й строки, принадлежащие соответствующим столбцам в (1.2), при любом выборе первых m значений последней строки. Т.е. для последней строки имеем
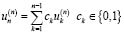 или (1.3)
или (1.3)
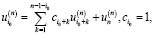
(cI=0 при I < I0)
при произвольных, начинающихся с единицы, первых m значениях этой строки. Это означает, что любое решение моноциклического оператора Ln является решением линейного разностного оператора порядка n–I0
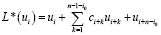 .
.
Действительно, пусть 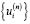 – решение моноциклического оператора Ln. Если в качестве последней строки в (1.2) взять любой участок этого решения, начинающийся с I, то получим (1.3). Возьмем произвольный участок длины n, начинающийся с нуля. Его, в силу того, что первые m значений можно выбирать произвольно, представим в виде суммы двух участков той же длины, начинающихся с I. А т.к. для этих участков выполняется (1.3), то (1.3) справедливо и для данного участка, начинающегося с 0. Т.е. при любых начальных значениях u1(n), u2(n), …, um(n) выполняется (1.3). А это и означает, что всякое решение моноциклического оператора Ln порядка m, является решением линейного разностного оператора L*(uI). Раз это так, то многочлен, соответствующий L*(uI) должен делиться на многочлен, соответствующий оператору Ln. Пусть
– решение моноциклического оператора Ln. Если в качестве последней строки в (1.2) взять любой участок этого решения, начинающийся с I, то получим (1.3). Возьмем произвольный участок длины n, начинающийся с нуля. Его, в силу того, что первые m значений можно выбирать произвольно, представим в виде суммы двух участков той же длины, начинающихся с I. А т.к. для этих участков выполняется (1.3), то (1.3) справедливо и для данного участка, начинающегося с 0. Т.е. при любых начальных значениях u1(n), u2(n), …, um(n) выполняется (1.3). А это и означает, что всякое решение моноциклического оператора Ln порядка m, является решением линейного разностного оператора L*(uI). Раз это так, то многочлен, соответствующий L*(uI) должен делиться на многочлен, соответствующий оператору Ln. Пусть
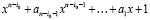 (1.4)
(1.4)
многочлен над полем GF(2), соответствующий оператору L*. Покажем, что если многочлен, соответствующий Ln,
xm+am–1xm–1 + … + a1x+1 (1.5)
является делителем многочлена (1.4), то он будет делителем некоторого многочлена большей степени, у которого нет в качестве слагаемых одночленов вида хk, где k≤ m, за исключением I.
Пусть (1.4) содержит в качестве слагаемого некоторый одночлен хk. где k≤ m (т.е. аk = I).
Умножая (1.4) на хk +I, получим многочлен степени n–I0 + k, у которого коэффициент при хk , т.е. аk=0. Аналогично можно поступить с любым слагаемым степени не большей m. Получим многочлен, у которого степень предпоследнего члена больше m, а максимальная степень самого многочлена равна 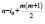 , т.е.
, т.е.
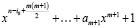 . (1.6)
. (1.6)
Если многочлен (1.5) делит (1.4), то он должен делить и многочлен (1.6). С другой стороны (1.6), как и многочлен (1.4), содержит четное число слагаемых, т.к. по условию этой леммы одна из строк (1.2) состоит из единиц. Поэтому (1.6) можно представить в виде суммы двучленов (P>0)
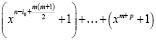 (1.7)
(1.7)
Разделим каждый из этих двучленов на (1.5). Т.к. (1.5) соответствует моноциклическому оператору Ln порядка m, то, согласно [1], является делителем двучлена (x2m-1+I), но не является делителем никакого двучлена xs+1, где s<2m–I. Но в силу леммы 1 степень многочлена (1.6) меньше 2m–I. Поэтому, разделив почленно (1.7) на (1.5), получим
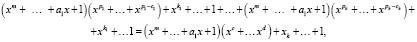
где kI<m, k<m. Остаток от деления,
хk+ …+1≠0 (mod 2), т.к. при делении каждого из двучленов (1.7) на (1.5) остаток содержит 1.Двучленов – нечетное число, поэтому суммарный остаток также содержит I. Таким образом, многочлен (1.6) не делится на многочлен (1.5).Противоречие.
Теорема 1. Существуют такие начальные условия для первых столбцов направляющих матриц, что последовательность точек РI=(P1(I), … Pn(I)), построенная по последовательности всех взятых подряд моноциклических операторов, при каждом n обладает свойством А.
Доказательство. Доказательство проведем по индукции. Легко проверить, что теорема справедлива до n = 7 (m(8)=5). Пусть она справедлива при некотором n>7. Но это означает, что выполняются условия лем-
мы 2. И если рассмотреть любой моноциклический оператор Ln+1 , порядок которого такой же, как у Ln или на единицу больше, то в силу леммы 2 ,у решения этого оператора найдется начинающийся с I участок длины n+I, такой что
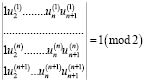 (1.8)
(1.8)
При этом все угловые определители (1.8) равны I (mod 2). Как следует из [2], это доказывает справедливость теоремы при n+I. Теорема доказана.
Построение новых ЛПτ-последовательностей. В [1] приводится следующий результат. Если в качестве в матрицы направляющих числителей взять такую, у которой все угловые определители равны 1(mod 2), то определенная этой матрицей ДР – последовательность будет ЛП0-последовательностью.
Возникает вопрос нельзя ли из таких последовательностей, определяющих значения различных коордитат многомерных точек, построить ЛПτ-последовательность? Приводимые ниже результаты дают возможность обобщить на рассматриаемый случай теорему из [1], в которой приводится конструкция ЛПτ-последовательности.
Пусть L – моноциклический оператор порядка m. Рассмотрим последовательность операторов L, L2, Ln,… . Каждому оператору Ln в этой последовательности поставим в соответствии его m линейно независимых решений
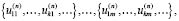 (2.1)
(2.1)
причем любое решение оператора Ln не является решением оператора Ln–1.
При этом первые nm элементов в каждой из последовательностей (2.1) выбраны так, чтобы в матрице
 (2.2)
(2.2)
все угловые определители были равны 1(mod 2). Положим, что 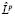 – произвольная степень отличного от L моноциклического оператора
– произвольная степень отличного от L моноциклического оператора 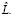
Лемма 1. Операторы 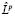 и Lk не имеют общих решений.
и Lk не имеют общих решений.
Доказательство. Действительно, пусть
{uI} – одна из последовательностей в (2.1) такая, что Lk(uI) =0. Тогда если бы имело место 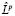 (ui) =0, то Lk–1
(ui) =0, то Lk–1 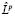 (ui) =
(ui) = 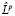 Lk–1 (ui) = 0. А это не так потому, что Lk–1(uI) – есть не тривиальное решение моноциклического оператора L. Вследствие леммы 4 параграфа 2 из [1], оно не может быть решением оператора
Lk–1 (ui) = 0. А это не так потому, что Lk–1(uI) – есть не тривиальное решение моноциклического оператора L. Вследствие леммы 4 параграфа 2 из [1], оно не может быть решением оператора 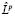 .
.
Лемма 2. Результат действия оператора 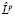 на любые n (n
на любые n (n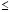 m) линейно независимые решения оператора Lk есть n линейно независимые решения оператора Lk–1.
m) линейно независимые решения оператора Lk есть n линейно независимые решения оператора Lk–1.
Доказательство. Покажем сначала, что 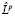 сохраняет линейную независимость решений оператора Lk. Подействуем оператором
сохраняет линейную независимость решений оператора Lk. Подействуем оператором 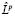 на n решений оператора Lk. Т.к.
на n решений оператора Lk. Т.к. 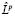 линейный оператор, то линейная зависимость полученных решений означала бы, что
линейный оператор, то линейная зависимость полученных решений означала бы, что 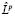
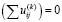 , I = 1,2,3,… .
, I = 1,2,3,… .
Но 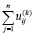 есть не тривиальное решение Lk в силу линейной независимости n выбранных решений. А т.к. решение Lk не может быть решением
есть не тривиальное решение Lk в силу линейной независимости n выбранных решений. А т.к. решение Lk не может быть решением 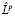 ,то полученные решения линейно независимы. Теперь подействуем оператором L на рассматриваемые решения оператора Lk. Понятно, что таким образом получим n решений оператора Lk–1. Они линейно независимы. Действительно, обратное означает, что
,то полученные решения линейно независимы. Теперь подействуем оператором L на рассматриваемые решения оператора Lk. Понятно, что таким образом получим n решений оператора Lk–1. Они линейно независимы. Действительно, обратное означает, что
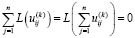 .
.
Сумма 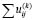 не есть решение оператора L, т.к. матрица (2.2) содержит все m линейно независимых решений оператора L. Если бы
не есть решение оператора L, т.к. матрица (2.2) содержит все m линейно независимых решений оператора L. Если бы 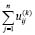 была решением оператора L, то она выражалась бы линейно через эти m решений. Но это находится в противоречии с условием, что все угловые определители в (2.2) были равны 1(mod 2).
была решением оператора L, то она выражалась бы линейно через эти m решений. Но это находится в противоречии с условием, что все угловые определители в (2.2) были равны 1(mod 2).
Теорема 2. Пусть L1, L2,…, Ln – различные моноциклические операторы, порядки которых равны m1, m2,…, mn. Каждому оператору Lk поставим в соответствие матрицу (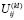 ), аналогичную (2.2). Пусть {PI} – последовательность точек с координатами, определяемыми этими матрицами, в соответствии с [1]. Тогда PI= (P1(I),…, Pn(I)) – есть ЛПτ-последовательность в единичном кубе Kn со значениями
), аналогичную (2.2). Пусть {PI} – последовательность точек с координатами, определяемыми этими матрицами, в соответствии с [1]. Тогда PI= (P1(I),…, Pn(I)) – есть ЛПτ-последовательность в единичном кубе Kn со значениями
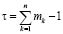 .
.
Доказательство. Cогласно доказательству указанной выше теоремы 4 из [1], для того, чтобы произвольный двоичный участок последовательности длины 2v был Пτ-сеткой необходимо и достаточно, чтобы ранг матрицы
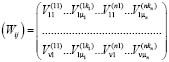 , (2.3)
, (2.3)
составленной из 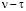 столбцов матриц направляющих чисел, соответствующих различным моноциклическим операторам, был равен
столбцов матриц направляющих чисел, соответствующих различным моноциклическим операторам, был равен 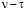 . Обозначим через
. Обозначим через 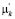 остаток от деления
остаток от деления 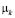 на mk так, что
на mk так, что 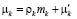 .
.
Пусть 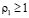 . Оставим в (2.3) первые m1 строк без изменений, а остальные будем заменять линейными комбинациями строк в соответствии с действием оператора L1. Получим эквивалентную матрицу
. Оставим в (2.3) первые m1 строк без изменений, а остальные будем заменять линейными комбинациями строк в соответствии с действием оператора L1. Получим эквивалентную матрицу
 . (2.4)
. (2.4)
В верхнем углу, согласно условию теоремы, находится невырожденная матрица. Нетрудно видеть, что столбцы 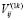 ,
,
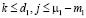 , являющиеся участками решений оператора L1, линейно независимы. Если
, являющиеся участками решений оператора L1, линейно независимы. Если 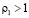 , то в нижней части матрицы (2.4) повторяем то же преобразование
, то в нижней части матрицы (2.4) повторяем то же преобразование 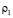 раз. Если
раз. Если 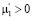 , то после этих преобразований останутся
, то после этих преобразований останутся 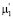 столбцов с элементами
столбцов с элементами 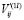 . Перенесем их в конец матрицы. Получим следующую мат-
. Перенесем их в конец матрицы. Получим следующую мат-
рицу
 (2.5)
(2.5)
Согласно лемме 2, 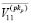 ,
, 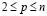 , есть участки решений оператора
, есть участки решений оператора 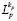 .
.
В силу этой леммы, столбцы 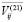 ,
, 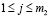 , образуют матрицу
, образуют матрицу
 ,
,
определитель которой равен 1. Посредством L2 c нижней частью матрицы (2.5) (расположенной под В1) проделаем преобразования, аналогичные предыдущим. Оставшиеся 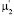 столбцов перенесем в конец матрицы. Проделав такие же преобразования со всеми Lk, получим матрицу
столбцов перенесем в конец матрицы. Проделав такие же преобразования со всеми Lk, получим матрицу
 (2.6)
(2.6)
Здесь 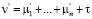 и элементы остаточной матрицы
и элементы остаточной матрицы
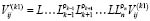 . (2.7)
. (2.7)
Если бы все 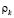 были равны 0, то исходная матрица уже имела бы вид (2.6).
были равны 0, то исходная матрица уже имела бы вид (2.6).
Ввиду того, что в (2.7) 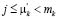 , то
, то 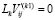 . Значит, столбцы остаточной матрицы – это участки решений моноциклических уравнений. Пусть среди
. Значит, столбцы остаточной матрицы – это участки решений моноциклических уравнений. Пусть среди 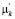 всего s чисел, отличных от нуля. Обозначим их через
всего s чисел, отличных от нуля. Обозначим их через 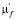 ,
, 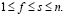 Все решения
Все решения 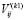 ,
,
соответсвующие одному f, линейно независимы в силу леммы 2.
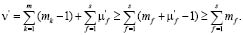
Поэтому из леммы 7 параграфа 3 [1] следует, что все столбцы остаточной матрицы линейно независимы, т.е., что ее ранг равен 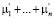 . А ранг всей матрицы равен
. А ранг всей матрицы равен 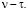 Теорема доказана.
Теорема доказана.
Библиографическая ссылка
Матусов И.Б. ОБ ОДНОМ СВОЙСТВЕ РАВНОМЕРНОСТИ И НОВЫХ ЛПτ-ПОСЛЕДОВАТЕЛЬНОСТЯХ // Успехи современного естествознания. 2014. № 5-2. С. 135-140;URL: https://natural-sciences.ru/ru/article/view?id=33941 (дата обращения: 05.03.2026).



