Введение
По статистике, сердечно-сосудистые заболевания являются одной из основных причин инвалидности и смерти жителей большинства современных развитых стран [3]. На долю смертности от заболеваний сердечно-сосудистой системы в общем приходится до 60% от общего числа умерших.
Нередко для восстановления кровообращения в пораженных сосудах помимо медикаментозного лечения проводятся реконструктивные операции, и часто невозможно объективно оценить, какой тип оперативного вмешательства будет оптимальным для конкретного пациента, а также насколько близок будет кровоток в сосуде к нормальному после операции. Основная проблема при выполнении таких расчетов состоит в определении механических свойств стенок сосудов, параметров кровотока и др.
Еще одной важной проблемой при прогнозировании результатов лечения является скорость расчетов: как правило, большинство современных математических моделей требуют численного решения, причем во многих случаях вычисления получаются затратными по времени и требуют довольно мощные компьютеры [8]. При этом снижение времени расчетов путем упрощений может привести к неточности полученных результатов, что, безусловно, недопустимо [5].
Часто для численных расчетов применяют метод конечных элементов. Однако решение задач гемодинамики с помощью МКЭ требует больших затрат по времени [5].
Таким образом, актуальной является задача построения математической модели гемодинамики, которая бы достаточно полно описывала движение крови в кровеносных сосудах, учитывая взаимодействие жидкости со стенкой, и являлась легко адаптируемой под конкретного пациента.
Материалы и методы
Рассмотрим осесимметричное движение крови, которая принимается вязкой несжимаемой жидкостью, в круглом сосуде постоянного радиуса R. Движение происходит в цилиндрической системе координат (x, r, θ), причем ось x совпадает с осью симметрии потока [2]. Материал стенки считаем идеально упругим, изотропным.
Основная система уравнений динамики кровотока в гибких цилиндрических сосудах в таком случае будет иметь вид:
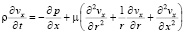 , (1)
, (1)
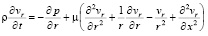 , (2)
, (2)
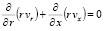 , (3)
, (3)
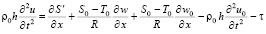 , (4)
, (4)
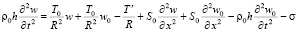 , (5)
, (5)
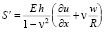 , (6)
, (6)
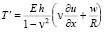 , (7)
, (7)
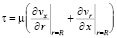 ,
, 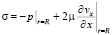 ,
,
где p – давление; ρ – плотность крови; μ – вязкость крови; vx – осевая компонента скорости крови; vr – радиальная компонента скорости крови; R – радиус сосуда; t – время; u, w – перемещения стенки в продольном и поперечном направлениях; Sʹ, Tʹ – силы натяжения в окружном и продольном направлениях соответственно; S0, T0 – начальные значения сил натяжения в окружном и продольном направлениях; E – модуль Юнга стенки; ν – коэффициент Пуассона; h – толщина стенки сосуда; ρ0 – массовая плотность материала стенки сосуда.
На стенке записываем условия кинематического контакта стенки сосуда с жидкостью:
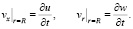 (8)
(8)
В случае моделирования гемодинамики крупных кровеносных сосудов в большинстве современных работ кровь полагается ньютоновской жидкостью [4, 7]. При этом в [6] показано, что разница значений (в случае крупных кровеносных сосудов), которые получаются для ньютоновской и неньютоновской жидкостей, не превышает 10%.
Уравнения (4)-(7) позволяют учесть податливость сосудистой стенки, а контактные условия (8) позволяют учесть взаимодействие стенки с потоком.
Такой подход к моделированию гемодинамики широко известен, однако основная система уравнений в этом случае не позволяет учесть конвективную составляющую ускорения частиц жидкости, а это, в свою очередь, для сосудистого русла с несколькими узлами бифуркации может оказать существенное влияние на результаты расчетов.
Основная система уравнений динамики вязкой несжимаемой жидкости в кровеносных сосудах с гибкими стенками в трехмерной постановке может быть записана в виде уравнений для направленных потоков.
Будем, как и раньше, полагать, что задача осесимметрична, а кровь является ньютоновской жидкостью.
Для направленных потоков жидкости в тонких трубках с упругими стенками на основе известного способа линеаризации возможен учет конвективного ускорения частиц жидкости в рамках линейной теории. В случае осесимметричных направленных потоков уравнения Навье-Стокса имеют следующий вид:
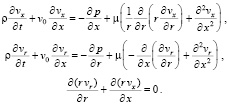 (9)
(9)
Здесь v0 – основная скорость направленного потока, вокруг которой происходит малая пульсация составляющих скоростей: vx = v0 + vʹ; vr = vʹ.
Динамические уравнения осесимметричных колебаний предварительно натянутой круглой цилиндрической оболочки записываются в виде:
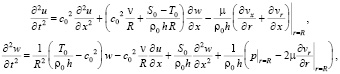 (10)
(10)
где 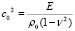 .
.
Условия «прилипания» частиц жидкости к стенкам сосуда заменим условием стесненного их скольжения по поверхности контакта:
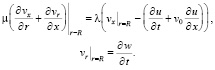 (11)
(11)
λ – коэффициент вязкого трения материала оболочки и жидкости.
Рассмотрим систему уравнений (9), (10) с контактными условиями (11). Умножим уравнение (1) на r и продифференцируем по x. Далее второе уравнение системы также умножим на r и продифференцируем по r, после чего сложим левые и правые части полученных уравнений. В результате получим уравнение для давления:
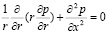 . (12)
. (12)
Запишем преобразованную систему уравнений:
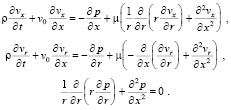 (13)
(13)
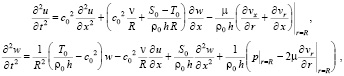
Для дальнейшего упрощения предложенной системы уравнений в трехмерной постановке можно вместо уравнений Навье-Стокса (9) использовать уравнения Эйлера для описания движения направленного потока идеальной несжимаемой жидкости, полагая при этом, что вязкое стесненное трение жидкости о стенку сосуда будет происходить в бесконечно тонком слое (погранслой) на контактной поверхности.
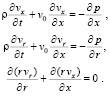 (14)
(14)
Вязкие свойства жидкости в погранслое будут описываться упрощенным одномерным уравнением, записанным на основании первого уравнения Навье-Стокса:
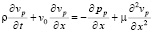 . (15)
. (15)
При этом на границе погранслоя функция давления может испытывать конечный скачок. Касательные напряжения на стенке будут иметь вид:
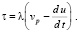 (16)
(16)
Тогда уравнения движения оболочки примут вид:
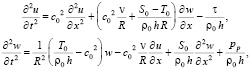 (17)
(17)
В качестве контактных условий для идеальной жидкости можно взять условия непроницаемости стенки и условия прилипания частиц жидкости вдоль стенки:
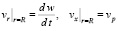 . (18)
. (18)
Из системы уравнений (14)-(17) путем простых преобразований может быть получено уравнение для давления в виде (12).
Запишем преобразованную систему уравнений:
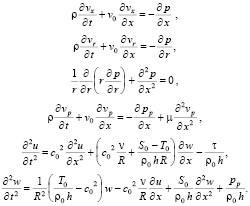 (19)
(19)
Система (19) с контактными условиями (18) представляет собой упрощенный вариант системы уравнений динамики кровотока в сосудах с упругими стенками, так как уравнения Навье-Стокса здесь заменяются уравнениями Эйлера для идеальной жидкости, которые имеют более простой вид.
Решение основной системы уравнений для случая пульсирующего кровотока как для системы (9)-(10), так и для системы (19) можно искать в виде простых гармонических волн:
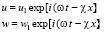 , (20)
, (20)
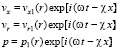 , (21)
, (21)
где ω – частота пульсации кровотока, χ – волновое число.
Подставляя выражения (21) в уравнения движения жидкости основной системы, получим базовые решения для амплитуд компонент скорости и давления. В этом случае сумма базовых решений для каждой волновой гармоники 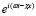 даст общее решение основной системы.
даст общее решение основной системы.
Неизвестные константы необходимо определять из контактных условий, уравнений движения стенки, а также из граничных условий на входе и выходах из сосудистой системы. Это напрямую связано с решением дисперсионных уравнений, возникающих при подстановке выражений (20) в основную систему.
Были получены начальные точки (рис. 1 и 2) дисперсионных кривых для дисперсионного уравнения, полученного при решении системы (1)-(7). На рисунках значения по осям а и b – это действительная и мнимая части волнового числа.
Используя полученные точки в качестве начальных приближений для построения решения дисперсионного уравнения, можно построить необходимые дисперсионные кривые, что позволит завершить решение полной краевой задачи с учетом краевых и контактных условий и найти необходимое число констант интегрирования.
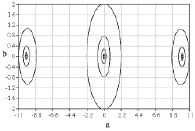
Рис. 1. Начальные точки дисперсионных кривых в случае малой вязкости
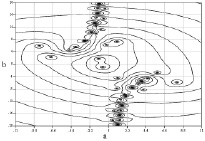
Рис. 2. Начальные точки дисперсионных кривых в случае большой вязкости
Такой алгоритм поиска общего решения системы (1)-(7) вполне подходит для решения систем (9)-(10) и (19). Таким образом, предложенные математические модели могут использоваться для исследования кровотока в системе кровеносных сосудов.
Результаты и обсуждение
Предложенные варианты постановки задач гемодинамики в системе кровеносных сосудов позволяют уменьшить количество основополагающих предположений и упростить основную систему уравнений. В случае, когда проводится учет направленных потоков жидкости, отпадает необходимость пренебрежения конвективной составляющей ускорения частиц, что повышает точность результатов.
Новый вид кинематических контактных условий стесненного скольжения (11), по мнению авторов, более адекватно описывает процесс взаимодействия потока со стенкой. В реальном сосуде в случае выполнения условий прилипания частиц неизбежным был бы процесс образования атеросклеротических отложений, который является патологическим. Таким образом, математические модели, в которых взаимодействие крови со стенкой описывается подобным образом, не могут достоверно описывать процесс гемодинамики.
Замена уравнений Навье-Стокса уравнениями Эйлера в системе (19) существенно упрощает основную систему, при этом уравнение для тонкого погранслоя вблизи стенки сосуда (15) позволяет учесть все возникающие в этой области процессы.
Таким образом, предложен ряд упрощений и уточнений, позволяющий более точно и адекватно моделировать движение крови в системе кровеносных сосудов человека.
Выводы
Предложены новые варианты постановки задач о движении крови в сосудах с упругими стенками, позволяющие уменьшить количество основополагающих гипотез и, тем самым, повысить строгость и реалистичность предлагаемых математических моделей.
Кроме того, предложен новый вид кинематических контактных условий, позволяющих более точно описать процесс взаимодействия потока крови с сосудистой стенкой.
Библиографическая ссылка
Доль А.В., Гуляев Ю.П., Иванов Д.В. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДВИЖЕНИЯ КРОВИ В СИСТЕМЕ СОСУДОВ С УПРУГИМИ СТЕНКАМИ // Успехи современного естествознания. 2014. № 9-1. С. 79-84;URL: https://natural-sciences.ru/ru/article/view?id=34193 (дата обращения: 15.02.2026).



