Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гапочкин А.В. 1 Барбарян В.Г. 1 Калмыков М.И. 1 Мартиросян А.Г. 1

---

1 ФГАОУ ВПО «Северо-кавказский федеральный университет»

Использование непозиционных модулярных кодов обусловлено тем, что данные алгебраические системы обладают свойством параллельности. Данные коды обеспечивают выполнение арифметических операций, к которым относятся операции сложения, вычитание и умножение, в реальном масштабе времени. Это обусловлено тем, что информация обрабатывается независимо по вычислительным каналам. Кроме повышения скорости обработки данных непозиционные модулярные коды способны обнаруживать и исправлять ошибки, которые могут возникнуть в процессе функционирования спецпроцессоров. Для выполнения процедур коррекции ошибок в статье предлагается использовать операцию расширения системы оснований.

Статья в формате PDF

2575 KB

модулярные коды

коды классов вычетов

система остаточных классов

обнаружение и коррекция ошибок

расширение системы оснований

1. Калмыков И.А., Калмыков М.И. Структурная организация параллельного спецпроцессора цифровой обработки сигналов, использующего модулярные код// Теория и техника радиосвязи. – 2014. – № 2. – С. 60–66.

2. Калмыков И.А., Воронкин Р.А., Резеньков Д.Н., Емарлукова Я.В., Фалько А.А. Генетические алгоритмы в системах цифровой обработки сигналов// Нейрокомпьютеры: разработка и применение. – 2011. – № 5. – С. 20–27.

3. Чипига А.Ф., Калмыков И.А. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности// Наука. Инновации. Технологии. – 2004. – Т. 38. – С. 46.

4. Калмыков И.А., Саркисов А.Б., Макарова А.В. Технология цифровой обработки сигналов с использованием модулярного полиномиального кода// Известия Южного федерального университета. Технические науки. – 2013. – № 12 (149). – С. 234–241.

5. Калмыков И.А., Резеньков Д.Н. Локализация ошибок в модулярных кодах полиномиальной системы классов вычетов с минимальной избыточностью// Фундаментальные исследования. – 2008. – № 3. – С. 23.

6. Калмыков И.А., Щелкунова Ю.О., Гахов В.Р., Шилов А.А. Математическая модель коррекции ошибок в полиномиальной системе класса вычетов на основе определения корней интервального полинома// Физика волновых процессов и радиотехнические системы. – 2002. – Т. 6, № 5. – С. 30.

7. Мартиросян А.Г., Калмыков М.И. Основные методы обеспечения отказоустойчивости специализированных вычислительных устройств цифровой обработки сигналов Современные наукоемкие технологии. – 2014. – № 3. – С. 62–67.

8. Барсагаев А.А., Калмыков М.И. Алгоритм обнаружения и коррекции ошибок в модулярных полиномиальных кодах// Международный журнал экспериментального образования. – 2014. – № 3–1. – С. 103–106.

9. Стрижков Н.С., Калмыков М.И. Алгоритм преобразования из модулярного кода в полиадическую систему оснований для систем обнаружения и коррекции ошибок // Международный журнал экспериментального образования. – 2014. – № 3–1. – С. 127–131.

10. Калмыков И.А., Саркисов А.Б., Яковлева Е.М., Калмыков М.И. Модулярный систолический процессор цифровой обработки сигналов с реконфигурируемой структурой// Вестник Северо-Кавказского федерального университета. – 2013. – № 2 (35). – С. 30–35.

Высокие требования к скорости обработки данных способствуют все более широкому применению параллельных вычислений. Особое место среди вычислительных систем реального масштаба времени занимают вычислительные устройства цифровой обработки сигналов (ЦОС). Так как в основу алгоритмов ЦОС положены операции сложения, вычитания и умножения, то в ряде работ было предложено использовать алгебраические системы, обладающие свойством кольца и поля [1–5]. Применение непозиционных модулярных кодов обеспечивает за счет параллельной работы с небольшими остатками обработку ЦОС с максимальным быстродействием.

Кроме этого независимая обработка остатков, отсутствие арифметических связей между вычислительными трактами непозиционного спецпроцессора (СП) ЦОС была положена в основу теории построения корректирующих модулярных кодов, которая приведена в работах [2-7]. Рассмотрим алгоритм поиска и коррекции ошибок в модулярном коде, который использует операцию расширения оснований.

Постановка задачи исследований

В настоящее время среди непозиционных модулярных кодов можно выделить две большие группы. Основу первой группы составляют непозиционные коды системы остаточных классов (СОК). При построении таких кодов классов вычетов в качестве оснований применяются взаимно простые числа [1–3]. Благодаря этому любой позиционный код можно представить в виде набора остатков, полученных при делении этого числа на числа-основания

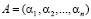, (1)

где ; .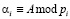

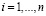Основу второй группы непозиционных кодов составляют модулярные полиномиальные коды, в частности коды полиномиальной системы классов вычетов (ПСКВ) [4-7]. При построении таких кодов классов вычетов в качестве оснований применяются неприводимые полиномы. Благодаря этому любой позиционный код, представляется в самом начале в полиномиальной форме, а затем полученному полиному в соответствие ставится набор остатков, полученных при делении этого числа на числа-основания

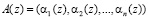, (2)

где ; .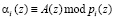

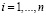Несмотря на различия, данные модулярные коды имеют много общего. Это во многом определяет сходство алгоритмов, которые используют данные коды классов вычетов. Следует отметить, что данные алгебраические системы применяют однотипные операции для осуществления поиска и коррекции ошибок, возникающих в процессе функционирования СП ЦОС.

Введение избыточности в модулярный код позволяет проводить процедуры, позволяющие при определенных условиях не только обнаруживать, но и исправлять ошибочные остатки.

В работах [1–3] приведены доказательства о величине минимальной избыточности, которую необходимо ввести в модулярный код, чтобы обеспечить коррекцию любой однократной ошибки. Так согласно этим работам выделение из общего набора n оснований двух контрольных оснований, таких что

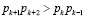, (3)

где k – количество рабочих оснований; ;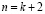

позволяет однозначно определить искаженный остаток и исправить его.

При этом, вводится следующее ограничение на количество разрешенных кодовых комбинаций. Если число А принадлежит рабочему диапазону, который определяется из условия

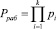, (4)

то его модулярный код не содержит ошибок.

Если число А не принадлежит рабочему диапазону, то есть

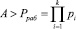, (5)

то его модулярный код СОК содержит ошибку.

Это обусловлено тем, что ошибка преобразует правильную комбинацию модулярного кода 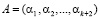в запрещенную комбинацию 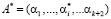, где 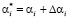– искаженный остаток, 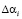– глубина ошибки. В этом случае перевод искаженного числа из рабочего диапазона, в диапазон полный. Поэтому во всех алгоритмах поиска и коррекции ошибок в модулярном непозиционном коде применяют позиционные характеристики [4–9]. Это позволяет узнать местоположение искаженной комбинации 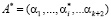в полном диапазоне, определяемым

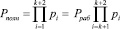. (6)

а затем однозначно определить основание, по которому произошла ошибка, а также ее глубину.

Одной из распространенных операций, позволяющих осуществить обнаружение и коррекцию кода класса вычетов, является расширение системы оснований. В основу данной операций положен алгоритм, который позволяет по значениям остатков по рабочим основаниям 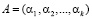вычислить значения остатков по двум контрольным основаниям, а затем их сравнить в исходными проверочными остатками.

В основу метода, базирующегося на вычислении синдрома ошибок по контрольным основаниям, положено определение разности между значениями остатков 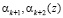по контрольным основаниям исходного числа 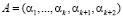и результатом вычисления остатков 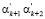с использованием рабочих оснований. Математически данный метод можно представить

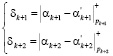(7)

где 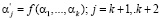; f – алгоритм вычисления остатков по рабочим основаниям.

В настоящее время вопросам разработки высокоэффективных методов расширения системы оснований модулярных кодов уделяется значительное внимание. В работе [7] был довольно подробно рассмотрен алгоритм расширения системы оснований. В основу данного алгоритма положена следующая математичес кая модель.

Если в упорядоченной системе остаточных классов с рабочими p1, p2,…, pk и контрольными основаниями pk+1, pk+2, удовлетворяющих условию (3), код СОК числа 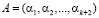не содержит ошибок, если выполняется условие

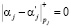, (8)

где

;

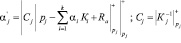Ra – ранг числа A в безизбыточной СОК;

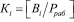; j=k+1,k+2.

Рассмотрим более подробно данный алгоритм. Известно, что интервальный номер l, в котором находится код СОК числа A определяется выражением

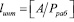. (9)

В то же самое время согласно китайской теореме об остатках (КТО) исходный код числа представляется

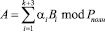. (10)

Подставив последнее равенство в выражение (9) и, воспользовавшись свойством сравнимости ортогональных базисов полной и безизбыточной системы остаточных классов, получаем

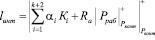, (11)

где

; ;

.

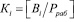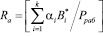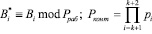Положим, что Рконт = pj, j=k+1,…,k+r. Тогда (11) примет вид

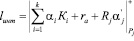(12)

Если полином 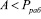>, то интервальный номер будет равен нулю 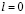. Следовательно, справедливо

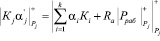(13)

Тогда

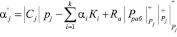, (14)

где .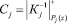

Таким образом, на основании (14) было произведено вычисление остатков 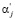по контрольным основаниям на основе известных значений .

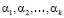Следовательно, если выполняется условие

,

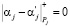то полином 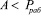, и он не содержит ошибки.

Рассмотренный алгоритм коррекции ошибок непозиционного кода системы остаточных классов с двумя контрольными основаниями позволяет исправлять все однократные ошибки и обнаруживать все двукратные ошибки.

Выводы

Современные непозиционные модулярные коды позволяют обеспечить цифровую обработку сигналов в реальном масштабе времени. При этом данные коды имеют аналогичные алгоритмы выполнения модульных и немодульных операций. В работе приведена математическая модель поиска и коррекции ошибок, использующая операцию расширения системы оснований. Проведенные исследования показали, что использование данного алгоритма позволяет исправить все однократные ошибки при использовании двух контрольных оснований.

Библиографическая ссылка