Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Голошубов К.С. 1 Солодкин И.Г. 1 Гапочкин А.В. 1 Калмыков М.И. 1

---

1 ФГАОУ ВПО «Северо-кавказский федеральный университет»

Современные модулярные коды нашли широкое применение во многих сферах деятельности человека. Среди таких областей можно выделить цифровую обработку сигналов, построение отказоустойчивых вычислительных устройств, способных сохранять работоспособное состояние при возникновении отказов, криптографические алгоритмы защиты данных. Одной из обязательных операций при использовании модулярных кодов является вычисление ранга. В работе представлен усовершенствованный алгоритм вычисления данной характеристики, а также нейросетевая схемная реализация.

Статья в формате PDF

2604 KB

модулярные коды

система остаточных классов

полиномиальная система классов вычетов

ранг

нейронные сети

1. Калмыков И.А., Калмыков М.И. Структурная организация параллельного спецпроцессора цифровой обработки сигналов, использующего модулярные код// Теория и техника радиосвязи. – 2014. – № 2. – С. 60–66.

2. Чипига А.Ф., Калмыков И.А. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности// Наука. Инновации. Технологии. – 2004. – Т.38. – С. 46.

3. Калмыков И.А., Воронкин Р.А., Резеньков Д.Н., Емарлукова Я.В., Фалько А.А. Генетические алгоритмы в системах цифровой обработки сигналов// Нейрокомпьютеры: разработка и применение. – 2011. – № 5. – С. 20–27.

4. Калмыков И.А., Саркисов А.Б., Макарова А.В. Технология цифровой обработки сигналов с использованием модулярного полиномиального кода// Известия Южного федерального университета. Технические науки. – 2013. – № 12 (149). – С. 234–241.

5. Мартиросян А.Г., Калмыков М.И. Основные методы обеспечения отказоустойчивости специализированных вычислительных устройств цифровой обработки сигналов Современные наукоемкие технологии. – 2014. – № 3. – С. 62–67.

6. Калмыков И.А., Саркисов А.Б., Яковлева Е.М., Калмыков М.И. Модулярный систолический процессор цифровой обработки сигналов с реконфигурируемой структурой// Вестник Северо-Кавказского федерального университета. – 2013. – № 2 (35). – С. 30–35.

7. Калмыков И.А., Чипига А.Ф., Кихтенко О.А., Барильская А.В. Криптографическая защита данных в информационных технологиях на базе непозиционных полиномиальных систем// Известия Южного федерального университета. Технические науки. – 2009. – Т. 100, № 11. – С. 210–220.

8. Калмыков И.А., Дагаева О.И. Новые технологии защиты данных в электронных коммерческих системах на основе использования псевдослучайной функции// Известия Южного федерального университета. Технические науки. – 2012. – Т. 137, № 12 (137). – С. 218–224.

9. Калмыков И.А., Стрекалов Ю.А., Щелкунова Ю.О., Кихтенко О.А., Барильская А.В. Технология нелинейного шифрования данных в высокоскоростных сетях связи// Инфокоммуникационные технологии. – 2010. – Т. 8, № 2. – С. 14–22.

10. Чипига А.Ф., Калмыков И.А., Яковлева Е.М., Калмыков М.И. Применение полиномиальной системы классов вычетов в схеме разделения секрета// Информационное противодействие угрозам терроризма. – 2012. – № 19. – С. 45–49.

Информационные технологии (ИТ) находят все большее применение в различных областях современного общества. Это обусловлено тем, что ИТ позволяют повысить эффективность работы специалистов во множестве отраслей хозяйства. Наиболее широкое применение IT-технологии нашли в области инфотелекоммуникационных систем. Особое внимание в таких системах уделяется цифровой обработке сигналов (ЦОС). Для обеспечения реального масштаба времени обработки сигналов применяются параллельные алгоритмы вычислений.

Обеспечить высокие требования к производительности вычислительных устройств возможно только за счет реализации алгоритмов ЦОС на основе специализированных процессоров (СП).

Высокие требованиями, предъявляемые к скорости обработки информации, обеспечили широкое использование параллельных алгоритмов вычислений в современных специализированных процессорах. Одним из перспективных направлений, позволяющим построить СП ЦОС реального масштаба времени, является использование непозиционных модулярных кодов [1–4]. Все множество модулярных кодов можно разбить на две группы. Основу первой группы составляют алгебраические структуры, обладающие свойством кольца. К ним можно отнести систему остаточных классов (СОК). В данной системе используются взаимно простые числа, которые выступают в роли оснований СОК. Тогда набор этих оснований образует рабочий диапазон

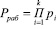. (1)

где pi – основания системы остаточных классов.

В этом случае, числа, которые принадлежат рабочему диапазону, можно однозначно представить в виде набора остатков

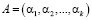, (1*)

где. – А < Pраб; .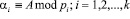

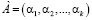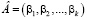Пусть даны два числа, представленные в коде СОК и . Тогда для суммы, разности и произведения двух чисел А и В, имеющих соответственно модулярные коды и справедливы соотношения при i = 1,…,k

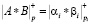, (2)

где * – операции сложения, вычитания и умножения по модулю.

Тогда ортогональное преобразование сигнала и ему обратное преобразование будут определяться

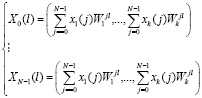, (3)

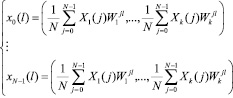, (4)

где W – поворачивающий коэффициент дискретного преобразования Фурье хi (j) ≡ x(j) mod pi – остаток по модулю отсчета входной последовательности x = {x(0), x(1),..., x(N – 1); Хi(j) ≡ Хi(j) mod pi – остаток по модулю спектрального отсчета сигнала .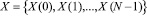

Основу второй группы составляют алгебраические структуры, работающие в кольце полиномов. К ним можно отнести полиномиальную систему классов вычетов (ПСКВ). В данной системе используются неприводимые полиномы pi(z), которые выступают в роли оснований GCRD. Тогда набор этих оснований образует рабочий диапазон

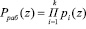. (5)

В этом случае, двоичный код числа представляется в полиномиальной форме. Тогда при выполнении условия deg А < deg Pраб, можно однозначно представить в виде набора остатков

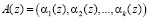, (6)

где – α_i (z) ≡ A(z) mod pi (z); i = 1, 2,...,k.

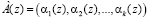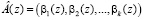Пусть даны два числа, представленные в коде ПСКВ и . Тогда для суммы, разности и произведения двух чисел А(z) и В(z), имеющих соответственно модулярные коды и справедливы соотношения при i = 1,…,k

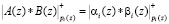, (7)

где * – операции сложения, вычитания и умножения по модулю.

Так как эти модулярные коды работают с остатками, то благодаря малоразрядности обрабатываемых остатков, реализация вычислений проводится в реальном масштабе времени. При этом такие вычисления осуществляются параллельно по независимым вычислительным каналам, которые определяются модулями кода. Благодаря этому модулярные коды нашли широкое применение не только в области цифровой обработки сигналов [1–3], построения отказоустойчивых вычислительных устройств [4–6], но и при реализации алгоритмов защиты данных от НСД [7–10].

Одним из основных факторов, снижающих эффективность применения непозиционных систем счисления, является отсутствие высокоэффективного алгоритма преобразования от ПСКВ к двоичному виду. Поэтому в настоящее время особое внимание уделяется разработке методов, обладающих параллельно-конвейерной структурой, которые бы позволили бы свести операцию преобразования кодов классов вычетов к позиционному на основе выполнения модульных операций.

Как правило, восстановление полученного результата из непозиционной системы счисления к двоичному позиционному виду на основе китайской теоремы об остатках (КТО) согласно

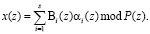(8)

Основным недостатком данного выражения является необходимость выполнения операции суммирования парных произведений по модулю P(z) . При значительных значениях динамического диапазона P(z) построение сумматора по модулю P(z) проблематично.

Одним из путей решения данной проблемы является вычисление ранг числа – K(z). Тогда выражение (8) преобразуется к виду

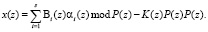(9)

Исходя их условия взаимной простоты модулей 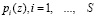, и равенства (9.) очевидно, что K(z) является целочисленной функцией, определяемой из значений x(z).

В отличие от выражения (8) , в котором значения x(z) нельзя вывести за пределы кольца P(z), равенства (9) осуществляет смещение значения x(z) за пределы этого диапазона P(z). На рис. 1 представлена геометрическая интерпретация выражений (8) и (9). Если диапазон P(z) представить в виде окружности, то равенства (9) может быть описано спирально, с радиусом равным радиусу P(z).

Рис. 1. Геометрическая модель: а) – выражения (8); б) – выражения (9)

Если x(z) является элементом P(z), то значение ранга K(z), должно удовлетворить условию

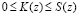(10)

где 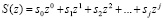– полиноминальное представление S.

Следовательно, величина K(z) не зависит от величины оснований 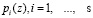, а определяется только их количеством. Таким образом, для определения величины ранга K(z) удовлетворяющего условию (10), целесообразно ввести дополнительное основание pg(z), которое обеспечивает выполнение следующего равенства

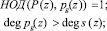(11)

где 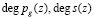– порядок полиномов pg(z) и s(z) соответственно.

Введение дополнительного модуля pg(z) обеспечивает выполнение 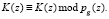(12).

(12)

Тогда из выражения (9), разделив обе части на P(z), получаем

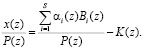(13)

Используя полученное равенство (13), а также условия (12), имеем

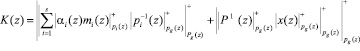, (14)

где mi(z) – вес i-го ортогонального базиса, такой что .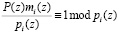

Таким образом, для вычисления значения ранга K(z) необходимо определить значения

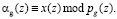(15)

Следовательно, исходный полином x(z) можно представить в виде 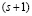–мерного вектора

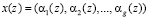. (16)

При этом дополнительный модуль pg(z) не входит в состав ПСКВ и не оказывает влияние на величину диапазона P(z). Если 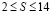, что чаще всего оправдывает себя выбор pg(z), порядок которого не превышает четырех. Следовательно, для реализации (15) не требуется значительных аппаратных затрат.

Таким образом, надо определить величину ранга K(z) согласно (14), а затем на основании выражения (9) осуществить перевод x(z) из ПСКВ в позиционную систему счисления.

Пример 1. Пусть задано расширенное поле Галуа 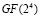, которое определяется следующими основаниями:

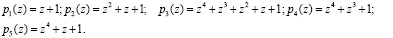
Полный диапазон системы составляет

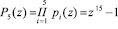
При этом ортогональные базисы данной алгебраической системы равны:

;

;

;

;

.

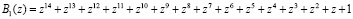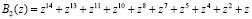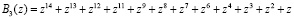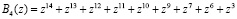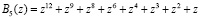Так число оснований s = 5, то в полиноминальной форме это сложно представить как s = z2 + 1. Тогда, согласно (11), выбираем дополнительное основание pg(z) = z3.

Воспользуемся выражением (9) и определим значение ранга K(z) полинома x(z) = z7 + z6 + z4 + z3 + z + 1, который в исходной ПСКВ представляется в виде

x(z) = (0, z + 1, z, z3 + z, z3 + z2 + z +1)

Для контроля рассчитаем преобразование ПСКВ в позиционную систему счисления по формуле (9)

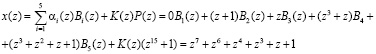
Откуда следует, что

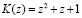
Найдем теперь значение ранга K(z), используя выражение (14). Очевидно, что для выбранной системы оснований значения 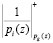, где i = 1, 2, 3, 4, 5, определяется следующим образом:

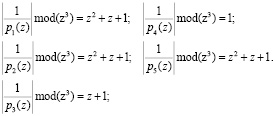
Значения весов ортогональных базисов полиномиальной системы классов вычетов поля GF(24), определяются как

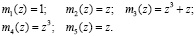
Так как дополнительное основание pg(z) = z3, то

.

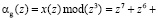
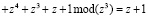Подставляя в равенство (9) полученные значения имеем

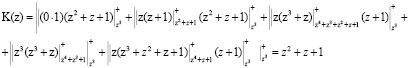
Полученное значение ранга K(z) совпадает со значением, непосредственно вычисляемым по формуле (9). Следовательно, предложенный алгоритм позволяет осуществлять выполнение операции вычисления ранга числа, используя только модульные процедуры. Нейросетевая реализация данного алгоритма приведена на рис. 2.

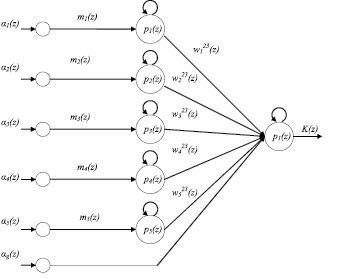
Рис. 2. Структура НС для вычисления ранга K(z)

Первый слой нейронной сети состоит из шести нейронов, которые осуществляют прием вектора

x(z) = (α1(z), α2(z), α3(z), α4(z), α5(z), α6(z)),

поданного на вход устройства. Синоптические веса связей 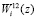, где i = 1, 2, 3, 4, 5, представляют собой веса ортогональных базисов 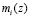и вычисляются заранее.

Результат умножения 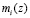и 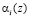преобразуется по модулю 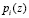во втором слое НС. Приведенные по модулю значения 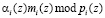, затем умножаются на 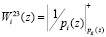, и совместно с добавочным остатком подаются на выходной слой НС, где и происходит сложение по модулю 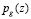. Полученный результат представляет собой ранг числа K(z).

Заключение

Применение модулярных кодов позволяет обеспечить обработку данных в реальном масштабе времени. Одной из обязательных операций, используемых при выполнении процедур обратного преобразования, а также поиска и коррекции ошибок, является вычисление ранга. В работе приведен алгоритм вычисления ранга, а также схемная нейросетевая реализация этого алгоритма.

Библиографическая ссылка