Квадратная матрица А третьего порядка вида
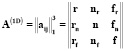
описывает множество вероятных структурных 1D состояний возможных детерминистических модулярных структур композитов. Множество состоит из трех основных состояний (rr ≡ r, nn ≡ n, ff ≡ f) и трех пар из взаимодополняющих (сопряженных) комплексных состояний (rn и nr, rf и fr, nf и fn). Матрица А вероятных структурных 1D состояний обладает следующими свойствами:
1 равенство сопряженной (А*) и транспонированной (АТ) матриц:
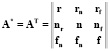
2) равенство дважды сопряженной и дважды транспонированной матрицы – исходной матрице:
(АТ)Т = (А*)* = А
3) наличие частичного порядка соподчинения вида
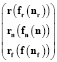 или
или 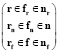
В случае детерминистических модулярных структур в каждой ячейке структурированного 3D пространства состояния определяются возможными кристаллическими r, наноразмерными n и фрактальными f компонентами [1–10]. С учетом всех структурно совместимых сочетаний из трех компонент можно перечислить десять классов вероятных структурных состояний [1, 2]: 1) (n n n), 2) (n n r), 3) (n n f), 4) (n f f), 5) (r f n), 6) (r r n), 7) (r r f), 8) (r f f), 9) (f f f) и 10) (r r r). Класс (r f n) – единственный класс возможных структурных состояний, представители которого включают в себя одновременно кристаллическую, фрактальную и наноразмерную компоненты. Возможные разложения данного состояния
(n r f) = (n n r) + (f f r),
(n r f) = (n r r) + (n f f),
(n r f) = (n n f) + (f r r),
(n r f) = (n n r) + (r r f) + (n f f),
(n r f) = (n r r) + (r f f) + (n n f),
(n r f) = (n n n) + (r r r) + (f f f)
позволяют рассматривать наряду с кристаллическими фазами квазифрактальные объекты, наночастицы и возможные промежуточные варианты между ними и могут служить аппроксимантами вероятных состояний на поверхности и в объеме композиционных материалов и покрытий.
Симметрия структур Rrfn3 может описываться пространственными G33 слоевыми G32, ленточными G32,1, точечными слоевыми G32,0 группами [11].
Перечислим возможные виды состояний класса (r f n), приведем соподчиненные () и сопряженные им (*) состояния.
1) (r f n) - 3D фрактальная структура из упорядоченных нанообъектов, (r f n)* = (r f n), (r f n) (nr nf n),
2) (r f nr) - 3D фрактал из упорядоченных 1D-нанофрагментов структуры, (r f nr)* = (r f rn), (r f nr) ( nr nf nr),
3) (r f nf) - 3D фрактал из упорядоченных 1D локальных фракталов, (r f nf)* = (r f fn), (r f nf) ( nr nf nf),
4) (r fn n) - 3D фрактальный нанообъект из упорядоченных 1D нанообъектов, (r fn n)* = (r nf n), (r fn n) (nr n n),
5) (r fn nr) - 3D фрактальный нанообъект из упорядоченных 1D-нанофрагментов структуры (r fn nr)* = (r nf rn), (r fn nr) (nr n nr),
6) (r fn nf) - 3D фрактальный нанообъект из упорядоченных 1D локальных фракталов, (r fn nf)* = (r fn nf), (r fn nf) (nr n nf),
7) (r fr n) - 3D структура из 1D детерминистических фракталов и упорядоченных нанообъектов, (r fr n)* = (r rf n), (r fr n) (nr nr n),
8) (r fr nr) - 3D структура из 1D детерминистических фракталов и упорядоченных 1D-нанофрагментов структуры, (r fr nr)* = (r rf rn), (r fr nr) (nr nr nr),
9) (r fr nf) - 3D структура из 1D детерминистических фракталов и упорядоченных 1D локальных фракталов, (r fr nf)* = (r rf fn), (r fr nf) (nr nr nf),
10) (rn f n) - 3D фрактальная структура из нанообъектов, упорядоченных в 1D пространстве нанофрагментов, (rn f n)* = (nr f n), (rn f n) (n nf n),
11) (rn f nr) - 3D фрактальная структура из 1D-нанофрагментов структуры, упорядоченных в 1D пространстве, (rn f nr)* = (nr f rn), (rn f nr) (n nf nr),
12) (rn f nf) - 3D фрактальная структура из 1D локальных фракталов, упорядоченных в 1D пространстве нанофрагментов, (rn f nf)* = (nr f fn), (rn f nf) (n nf nf),
13) (rn fn n) - 3D фрактальный нанообъект из 1D нанообъектов и упорядоченных в 1D пространстве нанофрагментов, (rn fn n)* = (nr nf n), (rn fn n) (n n n),
14) (rn fn nr) - 3D фрактальный нанообъект из 1D-фрагментов структуры и упорядоченных в 1D пространстве нанофрагментов, (rn fn nr)* = (nr nf rn), (rn fn nr) (n n nr),
15) (rn fn nf) - 3D фрактальный нанообъект из 1D локальных фракталов и упорядоченных в 1D пространстве нанофрагментов, (rn fn nf)* = (nr fn nf), (rn fn nf) (n n nf),
16) (rn fr n) - 3D структура из 1D детерминистических фракталов, нанообъектов и упорядоченных в 1D пространстве нанофрагментов, (rn fr n)* = (nr rf n), (rn fr n) (n nr n),
17) (rn fr nr) - 3D структура из 1D детерминистических фракталов, фрагментов структуры и упорядоченных в 1D пространстве нанофрагментов, (rn fr nr)* = (nr rf rn), (rn fr nr) (n nr nr),
18) (rn fr nf) - 3D структура из 1D детерминистических фракталов, 1D локальных фракталов и упорядоченных в 1D пространстве нанофрагментов, (rn fr nf)* = (nr rf fn), (rn fr nf) (n nr nf),
19) (rf f n) - 3D фрактальная структура из нанообъектов, упорядоченных в 1D пространстве по фрактальному закону, (rf f n)* = (fr f n), (rf f n) (nf nf n),
20) (rf f nr) - 3D фрактал из 1D-нанофрагментов структуры, упорядоченных в 1D пространстве по фрактальному закону, (rf f nr)* = (fr f rn), (rf f nr) (nf nf nr),
21) (rf f nf) - 3D фрактал из 1D локальных фракталов, упорядоченных в 1D пространстве по фрактальному закону, (rf f nf)* = (fr f fn), (rf f nf) (nf nf nf),
22) (rf fn n) - 3D фрактальный нанообъект из 1D нанообъектов, упорядоченных в 1D пространстве по фрактальному закону, (rf fn n)* = (fr nf n), (rf fn n) (nf n n),
23) (rf fn nr) - 3D фрактальный нанообъект из 1D-нанофрагментов структуры, упорядоченных в 1D пространстве по фрактальному закону, (rf fn nr)* = (fr nf rn), (rf fn nr) (nf n nr),
24) (rf fn nf) - 3D фрактальный нанообъект из 1D локальных фракталов, упорядоченных в 1D пространстве по фрактальному закону, (rf fn nf)* = (fr fn nf), (rf fn nf) (nf n nf),
25) (rf fr n) - 3D структура из 1D детерминистических фракталов и нанообъектов, упорядоченных в 1D пространстве по фрактальному закону, (rf fr n)* = (fr rf n), (rf fr n) (nf nr n),
26) (rf fr nr) - 3D структура из 1D детерминистических фракталов и 1D-нанофрагментов структуры, упорядоченных в 1D пространстве по фрактальному закону, (rf fr nr)* = (fr rf rn), (rf fr nr) (nf nr nr),
27) (rf fr nf) - 3D структура из 1D детерминистических фракталов и 1D локальных фракталов, упорядоченных в 1D пространстве по фрактальному закону, (rf fr nf)* = (fr rf fn), (rf fr nf) (nf nf n).
Таким образом, 27 видов реализации состояний класса (r f n) включают в себя все 10 видов соподчиненных им состояний наноразмерного класса (n n n) и имеют сопряженные с ними разновидности состояний из всех остальных девяти классов.
Условный размерный параметр D для каждого структурного состояния может быть рассчитан по одному из его возможных разложений следующим образом:
D = dr D(r) + df D(f) + dn D(n),
где dr, df и dn - количества соответствующих компонент одного сорта, условный размерный параметр для кристаллической компоненты D(r) = 1, для фрактальной компоненты он полностью совпадает с фрактальной размерностью:
D(f) = DimRf = Dim (GenRf) < 1,
для наноразмерной компоненты
D(n) = (<n>/no) < 1,
если средний размер нанообъекта <n> < no = 100 нм и D(n) = 1, если <n> no.
Пример. Определим размерный параметр для 27-ой разновидности состояния: (rf fr nf) - 3D структуры из 1D детерминистических фракталов и 1D локальных фракталов, упорядоченных в 1D пространстве по фрактальному закону. Сопряженным с ним состоянием является состояние (rf fr fn), представляющее собой 3D структуру из 1D детерминистических фракталов и 1D фрактальных нанообъектов, упорядоченных в 1D пространстве по фрактальному закону. С учетом разложения (rf fr fn) = 1/6 [2(r r r)+3(f f f)+(n n n)] окончательно получим
D = 1/6 [6 + DimGenRfff1 + DimGenRfff2 + DimGenRfff3 + 3(<n>/no)] < 3.
Таким образом, для любого структурного состояния класса (r f n), включающего только одну кристаллическую компоненту, значение условного размерного параметра D всегда будет меньше 3.
Соподчиненное состояние (n nf nf) представляет собой 3D-нанообъект из 2D локальных фракталов (фрактальных нанообъектов).
Ранее представления о возможном влиянии комплексного состояния композитов, обусловленного как кристаллическими фазами, так и распределенными определенным образом наночастицами некоторых из этих фаз, а также квазифрактальными характеристиками конфигураций межфазных границ, были использованы при целенаправленном поиске и интерпретации трибологических свойств поверхности композиционных материалов и покрытий на основе систем Ni-P и Ni-B [12-20].
Библиографическая ссылка
Иванов В.В. КОМПЛЕКСНЫЕ КОМПОНЕНТЫ СОСТОЯНИЙ КРИСТАЛЛИЧЕСКОГО ФРАКТАЛЬНОГО НАНОРАЗМЕРНОГО КЛАССА ДЕТЕРМИНИСТИЧЕСКИХ МОДУЛЯРНЫХ СТРУКТУР КОМПОЗИТОВ // Успехи современного естествознания. 2014. № 12-1. С. 90-92;URL: https://natural-sciences.ru/ru/article/view?id=34491 (дата обращения: 14.03.2026).



