В последнее время в научной литературе появилось ряд публикаций (см., например, [1-3]), в которых выполняются расчеты флуктуаций оптических волн при использовании неколмогоровских моделей для спектральной плотности флуктуаций показателя преломления атмосферы. К сожалению эти исследования, зачастую, выполнены без достаточного физического обоснования того почему появилось желание для проведения подобных расчетов.
Известно, что вся теория, описывающая распространение оптических волн в атмосфере базируется на законе (вообще говоря, на гипотезе) Колмогорова-Обухова [4, 5], при формулировке которого исходят из того факта, что в атмосфере можно считать стационарными не сами случайные величины (температура, скорость ветра, показатель преломления и др.), а только первые приращения этих величин, и поэтому для их описания применяются структурные функции. В частности, для флуктуаций температуры в атмосфере был предложен «закон 2/3», согласно которому, структурная функция температуры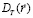 
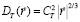, (1)
причем величина разноса точек наблюдения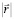 
должна удовлетворять следующим условиям:
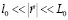, (2)
где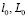 
– это внутренний и внешний масштабы атмосферной турбулентности.
В соответствии с этим законом, спектральная плотность флуктуаций показателя преломления атмосферы, оказывалась также степенной функцией во всем диапазоне масштабов. В научной литературе для учета влияния внутреннего масштаба турбулентности была предложена модель спектра [5], модифицированная, учетом влияния внутреннего масштаба турбулентности, Новиковым Е.А.
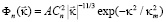. (3)
Здесь A – постоянная величина, а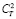 
– структурный параметр температуры, 
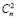– структурный параметр показателя преломления воздуха, 
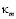– волновое число, соответствующее внутреннему масштабу турбулентности.
Именно эта модель (изотропного спектра) получила наибольшее применение при расчетах флуктуаций оптических волн, распространяющихся в турбулентной атмосфере. При этом, безусловно, предполагалось, что закон (1) выполняется для всех масштабов, что по умолчанию предполагает, что внешний масштаб турбулентности равен бесконечности, т.е. спектр (3) могут давать вклад неоднородности любого масштаба (размера). Спектр (3) позволял правильно рассчитывать [5] любые статистические характеристики флуктуаций интенсивности (амплитуды) оптических волн, распространяющихся в турбулентной среде в условиях «слабых» флуктуаций.
Проблема влияния конечности внешнего масштаба турбулентности
В тоже время всегда возникали вопросы в связи с тем, что для такого спектра был затруднен расчет энергии, поскольку оценка <<luk10.wmf>>во всем диапазоне масштабов (частот) расходится. В связи с этим постоянно имели место ограничения для расчета флуктуаций фазы оптической волны [6, 7]. В частности, спектр (3) Колмогорова-Обухова не позволял описывать такое явление как насыщение в поведении структурной функции фазы по мере увеличения расстояния между точками наблюдения. А выполненные в конце 70х годах XX века экспериментальные наблюдения [8-10] флуктуаций фазы оптического диапазона волн в приземном слое показали, что имеет место отклонение от рассчитанной с помощью модели (3) структурной функции фазы, имеет место насыщение. Объяснение этого эффекта [11-13] потребовало пересмотра применимости модели турбулентности Колмогорова-Обухова. Для расчета статистических характеристик Флуктуаций фазы оптической волны и ее модовых составляющих необходимо учитывать конечность внешнего масштаба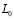 
турбулентности атмосферы. Для того чтобы описать это явление в литературе все более широкое применение получали модели [12-16] спектра изотропной атмосферной турбулентности, учитывающей конечность величины внешнего масштаба турбулентности 
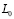, а именно,
– кармановская модель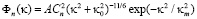 
(4)
– модель Гринвуда-Таразино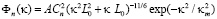 
(5)
– российская модель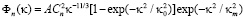 
(6)
Сопоставление этих моделей между собой и с данными экспериментов впервые сделано в работах [12, 14, 15]. Эти модели (4) –(6) уже недвусмысленно показывают важность внешнего масштаба для описания динамики оптических волн. Далее развитие понимания влияния спектров турбулентности стало распространяться на учет [17- 19] неизотропности спектра турбулентности вне инерционного интервала (2). Кроме этого впервые экспериментально [20] была получена зависимость величины внешнего масштаба от параметра термодинамической устойчивости атмосферы (число Монина-Обухова). При этом оказалось, что в приземном слое атмосферы ситуация следующая: самые большие значения величины внешнего масштаба реализуются при нейтральной стратификации, а как при устойчивой, так и при сильно неустойчивой стратификации внешний масштаб уменьшается. Для характеристики атмосферы в целом, по аналогии с радиусом когерентности Фрида, для описания флуктуаций оптических волн на вертикальных трассах был введен эффективных внешний масштаб турбулентности для атмосферы [21, 22].
Исследование турбулентности в условиях влияния подстилающей поверхности
Следующим аспектом проблемы, которой мы занимались был анализ влияния подстилающей поверхности. Эти многолетние исследования структуры атмосферной турбулентности были выполнены в рамках программы Сибирского отделения РАН «Астроклимат Сибири». Мы использовали как оптические измерения, так и метеорологические, с помощью акустической метеостанции с последующим теоретическим анализом экспериментальных спектров флуктуаций случайной температуры и компонент скорости.
В частности, эти экспериментальные данные измерений параметров турбулентности в различных географических районах и метеоситуациях стали обнаруживать существование в турбулентной атмосфере детерминированных образований – когерентных структур. Известно, что А.С. Монин и А.М. Яглом [4] определяют когерентную структуру как неслучайную нелинейную устойчивую суперпозицию крупномасштабных компонент турбулентности. Однако процесс распада гидродинамической ячейки, как установлено в наших работах [23-29], продолжается до самых мелких вихрей, которые могут существовать в воздухе. Поэтому в наших работах [24, 25] понятие «когерентная структура» было расширено.
Мы предлагаем гидродинамической когерентной структурой называть все компактное образование, включающее в себя как долгоживущую пространственную вихревую структуру (ячейку), возникающую в результате продолжительного действия термодинамических градиентов, так и продукты её дискретного когерентного каскадного распада. В расширенном понимании когерентная структура есть солитонное решение уравнений гидродинамики (топологический трёхмерный солитон, уединённая волна). Это либо односолитонное решение, либо один солитон в многосолитонном решении. Когерентная структура содержит как крупномасштабную, так и мелкомасштабную турбулентность. Турбулентность, возникающая в результате распада главного вихря, является когерентной и детерминированной [24-28].
Свойства одиночных когерентных структур
Свойства одиночных когерентных структур указаны и детально рассмотрены в наших статьях [24-28] и основные выводы на их основе следующие:
1. В результате действия термодинамических градиентов (температуры или давления) на границах некоторого выделенного объёма в жидкой среде возникает пространственная вихревая структура (ячейка, энергонесущий вихрь). Таких ячеек может быть одна или много. Ячейки представляют собой результат трансформации энергетических возмущений на границах объёма в движение жидкой среды. В нашем расширенном определении одна такая (обычно долгоживущая) ячейка вместе с продуктами дискретного когерентного каскадного распада самой этой ячейки называется когерентной структурой [4, 24, 25].
2. Распадающуюся пространственную структуру, представляющую собой главный энергонесущий вихрь, можно назвать порождающей ячейкой (структурой). Частота когерентно распадающегося главного вихря (порождающей ячейки) является основным признаком когерентной структуры.
3. Размеры когерентной структуры нечеткие. Течения, внешние по отношению к главному вихрю, могут переносить продукты его распада на значительные расстояния, образуя длинный турбулентный след.
4. Время жизни когерентной структуры определяется временем действия термодинамических градиентов (градиентов температуры и давления).
5. Как предельный случай сильной устойчивости, когерентная структура может состоять только из одной долгоживущей порождающей структуры. Тогда порождающая структура представляет собой некоторую конфигурацию ламинарного течения (нераспадающийся топологический солитон).
6. В конвективной когерентной структуре, возникающей в закрытом помещении, подтверждаются все основные сценарии возникновении турбулентности из ламинарных течений (сценарии стохастизации Ландау-Хопфа, Рюэлля-Таккенса, Помо-Манневилля, Фейгенбаума [4]). Главным сценарием является сценарий Фейгенбаума.
7. Распад главного энергонесущего вихря когерентной структуры осуществляется по сценарию Фейгенбаума. Главный вихрь в ячейке распадается на более мелкие в результате серии бифуркаций удвоения периода (в атмосфере – около десяти бифуркаций). Возникающая в результате турбулентность является когерентной и детерминированной.
8. Спектр пассивной примеси (температуры) в распадающейся ячейке фрактален (локально самоподобен).
9. Турбулентность, возникающая в когерентной структуре, как показано в наших работах [24-28] удовлетворяет всем признакам, характеризующим появление хаоса в типичных динамических системах. К этим признакам обычно относятся: возникновение нерегулярных долгоживущих пространственных структур, вид (характер) которых определяется диссипативными факторами, локальную неустойчивость и фрактальность фазового пространства таких структур, появление центрального (на нулевой частоте) пика в спектре. При этом центральный пик в спектре возникает, как установлено нами в [24-26]), за счёт нестационарности случайных процессов в когерентной структуре.
10. Известные процессы перехода ламинарных течений в турбулентные (конвекция Релея-Бенара, обтекание жидкостью препятствий и др.) можно считать процессами образования либо одиночных когерентных структур, либо образования сумм различных когерентных структур.
11. Когерентная структура содержит как крупномасштабную, так и мелкомасштабную турбулентность. При этом одномерный спектр турбулентности (компонент скорости и температуры) имеет более быстрое убывание в инерционном интервале (обычно 8/3-степенное убывание, которое в высокочастотной части инерционного интервала переходит в еще более сильное 12/3-убывание) по сравнению с колмогоровским 5/3-степенным убыванием.
12. Внешний масштаб турбулентности в одиночной когерентной структуре можно считать продуктом первого акта распада когерентно распадающегося главного вихря [24-28].
Модель спектра когерентной турбулентности
Для построения теоретической модели Φe(k) спектра когерентной турбулентности можно также использовать кармановскую модель с соответствующим убыванием в инерционном интервале. Такая приближенная модель спектра Φe(k) была получена в наших работах [24-26]:
FТ (k) = A0CТ 2(6.6κ0e)2(n – 1/3) k – 2(n + 3/2)exp(–κ2/κm2)[1– exp(–κ2/κ0e2], (7)
A0 = 0.033, κ0e = 2p/L0 , κm = 5.92/l0 ; n = 5/6, 1/3,
где CТ2 – структурная характеристика флуктуаций температуры, L0 и l0 – внешний (экспоненциальный) и внутренний масштабы турбулентности. Для некогерентной колмогоровской турбулентности n = 1/3, тогда в инерционном интервале FТ(k) ~ k– 11/ 3. В когерентной турбулентности n = 5/6, что в большей части инерционного интервала дает FТ (k) ~ k – 14/ 3. Дальнейшее, более быстрое, убывание спектра в вязком интервале описывается экспоненциальным множителем в (7). Максимальная погрешность аппроксимации реальных спектров выражением (7) в вязком интервале приходится на область очень больших частот.
Спектр (7) получен нами в [24-26] с учетом приближенной связи между внешними масштабами для n = 5/6 и n = 1/3 (в среднем они отличаются коэффициентом 2.3) и связи при n = 1/3 между кармановским внешним масштабом L0K и экспоненциальным L0 (обычно L0 = 0,54 L0K). Экспоненциальный спектр (7) отклоняется от кармановского (4) только в энергетическом интервале, где κ2 / κ02 << 1. Однако при n = 1/3 он дает практически такие же результаты, как и кармановский [27, 28]. В то же время он значительно упрощает расчеты.
Отметим, что максимальная погрешность аппроксимации реальных спектров выражением (7) в вязком интервале приходится на область очень больших частот. Поэтому в задачах распространения волн в турбулентной среде, в которых большую роль играет вязкий интервал, следует использовать модель, более подробную, чем (7). В задачах же, где основной вклад приходится на флуктуации фазы волны (смещения оптических пучков, дрожание изображений и др.) вязкий интервал не вносит существенного вклада, поэтому аппроксимация (7) применима.
Уменьшение флуктуаций оптических волн в когерентной турбулентности
В свою очередь, такая когерентная турбулентность обладает рядом интересных свойств. Так, например, в наших работах [29-31] впервые было показано, что по сравнению с некогерентной колмогоровской турбулентностью в когерентной турбулентности происходит значительное ослабление как амплитудных, так и фазовых (рефракционных) флуктуаций оптического излучения.
Такое заявление, безусловно, требует проведения экспериментальной проверки наличия эффекта ослабления флуктуаций света в атмосферной когерентной турбулентности. С этой целью были предприняты многолетние экспериментальные наблюдения в высокогорной Саянской солнечной обсерватории Института солнечно-земной физики СО РАН (п. Монды, Бурятия) в 2010-2014 гг. Полученные нами за многолетний период наблюдений метеорологические данные показывают [23 -27], что над территорией Саянской солнечной обсерватории часто наблюдаются крупные когерентные структуры. Поэтому именно здесь эффект ослабления флуктуаций света может быть зарегистрирован с большой вероятностью.
Наши измерения проводились на автоматизированном горизонтальном солнечном телескопе (АСТ). Измерялась дисперсия дрожания изображения края солнечного диска st2 в зависимости от диаметра приемного зеркала. Источником в эксперименте служил край солнечного диска. В качестве фотоприемника использовался известный датчик Брандта, являющийся фотоэлектрическим регистратором дрожания. Датчик Брандта прошел успешную апробацию в течение нескольких десятков лет и ранее применялся в аналогичных исследованиях рядом отечественных и зарубежных исследователей. Параллельно с оптическими измерениями с помощью ультразвуковой метеосистемой производился непрерывный контроль метеоситуации с определением типа турбулентности (когерентная или некогерентная колмогоровская турбулентность) вблизи приемного телескопа АСТ.
Результаты оптических и параллельных метеорологических измерений показали, что когда в атмосфере присутствуют крупные когерентные структуры (спектр флуктуаций температуры WT ~ f – 8/ 3, когерентная турбулентность), то наши данные совпадают с когерентной теорией (σa ~ const, точка 2 на рис. 1). В случае отсутствия в атмосфере крупных структур (некогерентная турбулентность, WT ~ f – 5/ 3) наши результаты совпадают с традиционной некогерентной теорией (наклонная линия и точки 1, 3 – 5 на рис. 1). Как видно из рис. 1, стандартное отклонение дрожания изображения края солнечного диска [30-31] в когерентной турбулентности значительно меньше, чем в случае некогерентной колмогоровской турбулентности.
Рис. 1. Среднеквадратическое отклонение σt дрожания астрономического изображения края солнечного диска в зависимости от диаметра входной апертуры телескопа 2at. Саянская солнечная обсерватория. Летние измерения 2010 г. Для экспериментальной точки 2at = 10 см – спектр WT ~ f – 8/ 3 , для других точек – WT ~ f – 5/3
Свойства смесей нескольких когерентных структур
Дальнейшие исследования были связаны с исследованием нескольких когерентных смесей. Свойства смесей (сумм) таких различных когерентных структур также были детально рассмотрены и изучены в наших статьях [23-28]. Ранее мы показали, что возможен следующий взгляд на процесс формирование колмогоровской турбулентности. В нашей работе [25] ранее уже было высказано предположение, что реальная атмосферная турбулентность представляет собой (некогерентную) смесь различных когерентных структур с несоизмеримыми частотами главных энергонесущих вихрей. Для доказательства этого был проведен следующий численный эксперимент: было взято четыре спектра вида (7) с различными величинами внешнего масштаба турбулентности, соответственно, 60, 30, 15 и 7.5 м. В результате суммирования был получен некий средний спектр (см. рис. 2), у которого появляется «инерционный» интервал, где наклон спектра несколько ниже, чем у каждого из когерентных спектров. Это подтверждает наше предположение, что колмогоровская турбулентность может быть сформирована как аддитивная сумма нескольких когерентных спектров.
В тоже время возможно путем сложения нескольких когерентных кармановских моделей спектра турбулентности вида (7) получать спектры с еще более медленным спаданием в »инерционном» участке спектра. В реальной атмосфере это вполне может происходить, например, в приземном слое при наличии больших неровностей постилающей поверхности. Подобные ситуации могут возникать в условиях гор [26, 29]. На наш взгляд, ключевым элементом формирования той или иной модели спектра является поведение основных «энергонесущих» масштабов, т.е., внешних масштабов турбулентности. Возможны ситуации, когда энергия в турбулентность поступает на различных масштабах, а также может реализоваться ситуация, когда имеет место существование преимущественно одна крупная структура, распад которой и обуславливает формирование когерентной турбулентности.
В результате многолетних (более 10 лет) экспедиционных измерений в различных климатических условиях и регионах с горной и ровной поверхностью нами накоплена обширная экспериментальная база данных приземных характеристик атмосферной турбулентности. Измерения проводились в Байкальской астрофизической обсерватории, Саянской солнечной обсерватории, в горах Колыванского Хребта, в горах Северного Кавказа и др. В атмосфере обычно наблюдаются когерентные структуры с главными вихрями разных размеров. Поэтому атмосферу можно рассматривать как среду, удобную для исследования характеристик смесей различных когерентных структур. Накопленные экспериментальные данные обрабатывались также с применением методов спектрального анализа случайных процессов.
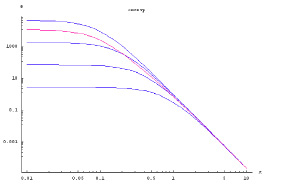
Рис. 2. Показан результат процесса образования колмогоровского спектра турбулентности (красная кривая) из нескольких (сумма 4-х) когерентных «кармановских» спектров, имеющих значения внешнего масштаба соответственно равные 60 м, 30 м, 15 м, 7.5 м (на рисунке кривые приведены сверху-вниз)
Сформулируем кратко основные свойства смесей различных когерентных структур.
1. В одной когерентной структуре продукты её распада образуют семейство вихрей, синфазных (когерентных) главному вихрю. В атмосфере обычно имеются разные когерентные структуры, у которых частоты главных вихрей неодинаковы (некратны, несоизмеримы). При смешивании таких разных когерентных структур элементы одного семейства будут несинфазны (некогерентны) элементам другого семейства. Поэтому турбулентность, возникающую при смешивании когерентных структур с главными вихрями разных размеров, естественно назвать некогерентной.
2. Турбулентность, наблюдающаяся в одной когерентной структуре (когерентная турбулентность) отличается от некогерентной колмогоровской более быстрым убыванием одномерного спектра турбулентности в инерционном интервале (обычно 8/3-степенное убывание вместо 5/3-колмогоровского убывания) и меньшим вкладом мелкомасштабных компонент.
3. Любой спектр турбулентности в атмосфере (для температуры и компонент скорости) представляется в виде суммы спектров разных когерентных структур с той же интенсивностью турбулентности, но имеющих разные размеры главных вихрей (различные внешние масштабы турбулентности). Поэтому турбулентность в открытой атмосфере можно рассматривать как сумму различных когерентных структур [25-29], имеющих разные размеры. Следовательно, реальную атмосферную турбулентность можно считать некогерентной смесью (суммой) различных когерентных структур с несоизмеримыми частотами главных энергонесущих вихрей.
4. При одинаковой интенсивности турбулентности кривая, соответствующая инерционному интервалу одномерного спектра колмогоровской турбулентности, является верхней огибающей суммы одномерных спектров разных когерентных структур, имеющих различные размеры главных энергонесущих вихрей (разные внешние масштабы) [29-31].
5. Если в рассматриваемой области среды разница между размерами главных вихрей разных когерентных структур невелика (не более 2 – 8 раз), то сумма спектров разных когерентных структур практически не отличается от колмогоровской зависимости. Если же эта разница велика (более 20 – 30 раз), то сумма спектров имеет глубокий провал, в котором «обнажается» спектр одной самой крупной структуры с 8/3-степенным убыванием. Турбулентность в этой области в таком случае называется когерентной.
6. Если в рассматриваемой области среды когерентные структуры имеют разные, но близкие размеры (отличающиеся не более, чем в 2 – 8 раз) и расположены сравнительно недалеко друг от друга («хорошо смешаны»), то наблюдается локальная изотропия турбулентности, описываемая колмогоровским спектром. Если же одна из когерентных структур существенно больше других (или же структуры значительно удалены друг от друга), то наблюдается анизотропия турбулентности, описываемая спектром турбулентности в одной когерентной структуре (спектром когерентной турбулентности).
7. При обтекании препятствий, вследствие постоянной генерации крупных ячеек и переноса продуктов их распада внешним течением, течения сразу за препятствиями обеднены мелкими вихрями. Поэтому, сразу за препятствием спектр флуктуаций соответствует когерентной турбулентности. С увеличением расстояния от препятствия, вихри (являющиеся продуктами распада) из турбулентных следов распадающихся когерентных структур смешиваются с окружающей турбулентной атмосферой, и турбулентность из когерентной постепенно переходит в колмогоровскую.
8. Системы порождающих ячеек-структур (системы солитонов, представляющих собой главные энергонесущие вихри) могут принимать различные формы: от уединенной упорядоченной структуры, типа тороидальной ячейки Бенара или типа произвольного осесимметричного вихря, до систем периодически распределённых в пространстве гидродинамических возмущений, типа систем разнообразных валов и др.
9. Размеры порождающих ячеек в атмосфере могут отличаться друг от друга в сотни миллионов раз: от нескольких сантиметров (пристеночная турбулентность, термики) до нескольких тысяч километров (ячейки Ферреля и Гадлея – ячейки общей циркуляции атмосферы).
10. Интересным случаем долгоживущей системы крупных порождающих ячеек в атмосфере можно считать циклоны и антициклоны (осесимметричные вихри с разными направлениями вращения, с достаточно сложной внутренней структурой, с размерами от 100 до 2000 км). По одиночке обычно не возникают, чаще образуют устойчивые четвёрки. Четвёрка устойчива именно из-за разных направлений вращения, так как в области соприкосновения циклона и антициклона воздух движется в одном направлении и давление здесь уменьшается. Внешнее давление стягивает их друг к другу. Образуется устойчивая структура – четырёхсолитонное решение уравнений гидродинамики. Разрушение циклона или антициклона происходит в течение нескольких суток и приводит к существенному усилению турбулентности в регионе. Об этом лётчиков обычно предупреждают диспетчерские службы аэропортов [26].
11. Когерентная турбулентность есть основная причина значительных отклонений постоянных Колмогорова и Обухова от своих стандартных значений. Как следствие, это приводит к большим (до 100 %) погрешностям в (основанных на законе Колмогорова-Обухова) измерениях характеристик турбулентности [24].
12. Другим источником ошибок в измерениях характеристик турбулентности служат структурные функции (флуктуаций температуры и компонент скорости). Нами показано, что по сравнению с колмогоровской турбулентностью в структурной функции температуры удлиняется начальный квадратический интервал (внутренний масштаб турбулентности в когерентной структуре на порядок больше колмогоровского), укорачивается инерционный 2/3-интервал (который проявляется лишь приближённо), появляется дополнительный коэффициент. Поэтому в измерениях из 2/3-асимптотики структурной функции интенсивность когерентной турбулентности будет завышенной более, чем в два раза.
13. В когерентной турбулентности по сравнению с колмогоровской происходит ослабление фазовых флуктуаций оптического излучения (вследствие обедненности мелкомасштабными неоднородностями). Поэтому, с целью повышения качества изображений, для установки наземных астрономических телескопов можно рекомендовать районы, над которыми во время измерений имеются области когерентной турбулентности.
14. Обедненность когерентной турбулентности мелкомасштабными неоднородностями (по сравнению с колмогоровской турбулентностью) приводит также к уменьшению (почти в два раза) интегральной интенсивности атмосферной когерентной турбулентности (интеграл по всем высотам от высотного профиля интенсивности турбулентности).
15. В высокогорных обсерваториях при переносе ветром сформировавшихся в атмосфере областей неколмогоровской когерентной турбулентности наблюдается неколмогоровский эффект перемежаемости дрожания астрономических изображений. Эффект заключается в периодическом ослаблении и усилении фазовых флуктуаций оптического излучения, и обусловлен наличием большого числа областей когерентной турбулентности с наветренной стороны (и их последующим ветровым переносом).
Таким образом, из вышеперечисленных свойств, как одиночных когерентных структур, так и смесей (сумм) различных когерентных структур, следует, что когерентную структуру (в расширенном определении), несмотря на её сложное внутреннее строение, можно рассматривать как основной базисный структурный элемент (как элементарную частицу), из которых состоит турбулентность.
Заключение
Сравнение установленных нами (и перечисленных выше) свойств структур с известными результатами показывает, что наши данные существенно расширяют существующие в настоящее время в мировой научной литературе представления о когерентных структурах.
1. Исследованы процессы возникновения когерентных структур в воздухе. Установлено, что распад главного энергонесущего вихря когерентной структуры осуществляется по сценарию Фейгенбаума. Показано, что возникающая в результате турбулентность является когерентной и детерминированной. Обнаружена фрактальность (локальное самоподобие) спектра турбулентности.
2. Применяемые нами методы спектрального анализа случайных функций позволили расширить известное определение когерентной структуры, с включением в ее состав мелкомасштабных неоднородностей среды. В расширенном понимании когерентная структура есть уединенное солитонное решение уравнений гидродинамики.
3. Показано, что реальная атмосферная турбулентность есть (некогерентная) смесь различных когерентных структур с несоизмеримыми частотами главных энергонесущих вихрей. Поэтому когерентную структуру можно рассматривать как структурный элемент, из которых состоит турбулентность.
4. В открытой атмосфере часто наблюдаются протяженные области, в которых определяющее влияние имеет одна крупная когерентная структура. Турбулентность в таких областях мы называем когерентной. В когерентной турбулентности наблюдается эффект ослабления флуктуаций света.
Полученные результаты можно рассматривать как новый взгляд на проблему турбулентности. Наши данные показывают, что турбулентность, в том числе и когерентную атмосферную турбулентность, следует рассматривать как результат действия самоорганизующихся нелинейных процессов в сплошных средах. Самоорганизующиеся процессы, как известно, обнаруживаются в различных областях естествознания. Поэтому наблюдение когерентных структур в других нелинейных системах представляет несомненный интерес.
Библиографическая ссылка
Лукин В.П., Носов В.В., Носов Е.В., Торгаев А.В. ПРИЧИНЫ ПРОЯВЛЕНИЯ НЕКОЛМОГОРОВСКОЙ ТУРБУЛЕНТНОСТИ В АТМОСФЕРЕ // Успехи современного естествознания. – 2014. – № 12-4. – С. 369-377;URL: https://natural-sciences.ru/ru/article/view?id=34614 (дата обращения: 19.04.2024).