Для исследования данной научной темы явилась необходимость оценки напряженно-деформированного состояния неоднородного упругоползучего грунтового основания при устройстве на нем песчаной подушки. А также из необходимости разработок методов для расчета грунтовых оснований с учетом их структурной прочности. Все это исходило из выяснения причины разрушения отдельных высотных сооружений, построенных в регионах Южного Казахстана. Несмотря на успешную эксплуатацию многих этих сооружений на подобных грунтах, в целом, на практике сталкиваемся с авариями и большими недопустимыми осадками грунтовых оснований. Причем анализ показывает, что причиной аварий является неправильное представление о физических и механических характеристиках самих грунтов. Кроме того, не учитываются такие свойства грунтов как неоднородность, вязкость, структурная прочность, проницаемость и др.
Следовательно, правильный подход к решению этих вопросов во всех случаях может облегчить строительство, ускорить сроки его осуществления и снизить стоимость самого сооружения. Вместе с тем, всякие ошибки в этом отношении могут быть чреваты последствиями. Здесь главное – правильно поставить задачу, особенно в случаях возведения крупных и ответственных сооружений, возводимых на водонасыщенных глинистых грунтах, учитывая при этом все необходимые условия, в которых они окажутся.
Следует заметить, что на сей день накопились многочисленные исследования по определению фактического напряженно-деформированного состояния грунтов водонасыщенных оснований. Установлены пределы применимости этих методов для расчета фундаментов и грунтовых оснований по теории линейно-деформируемых сред при совместной их работе. Однако думаем, что настало время решать такие задачи консолидации, расчетные формулы которых может позволить учесть ряд факторов, сильно влияющих на уплотнение массивов и, обеспечивают прочность любого здания и сооружения.
В связи с этим, для достижения наибольшего эффекта при решении указанных проблем, в данной статье в качестве деформируемого твердого тела рассматривается неоднородное грунтовое основание, обладающее вязким свойством. В настоящее время для описания вязкого свойства грунта часто применяют теорию ползучесть, разработанную Г.Н. Масловым – Н.Х. Арутюняном [3], в интерпретации В.А.Флорина [8]. Одновременный учет этих факторов, безусловно, приводит к новым качественным результатам в теоретических решениях, которые больше соответствуют результатам эксперимента. Уравнение в интегральной форме для одномерного состояния неоднородной грунтовой среды, подчиняющейся этой теории, имеет следующий вид:
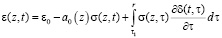, (1)
где функция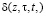 
, входящая в (1), находится из выражения
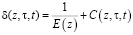; (2)
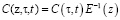– мера ползучести неоднородного грунта; 
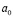– коэффициент сжимаемости; ε0 и e – коэффициенты пористости для начального и конечного моментов времени; 
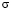– напряжение в скелете грунта; 
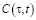– мера ползучести однородного грунта. Она определяется по формуле:
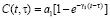. (3)
Здесь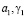 
– параметры ползучести; t – момент приложения внешней нагрузки.
В отличие (1) от [8], коэффициент сжимаемости здесь считается переменной величиной, и он зависит от глубины исследуемой точки уплотняемого массива.
Неоднородность грунтового массива учитывается через его модуль деформации, который в математическом виде может быть представлен в виде степенной [7]
(
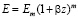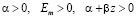), (4)
где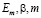 
являются опытными параметрами.
Далее рассмотрим процесс уплотнения слоя двухфазного грунта мощностью h под действием распределенной внешней нагрузки с интенсивностью q(z,t), мгновенно приложенной в момент времени t =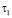 
. Пусть при этом верхняя поверхность уплотняемой грунтовой среды находится под песчаной подушкой, т.е. поверхность водопроницаема, а её нижняя поверхность водонепроницаема. Тогда граничные условия данной задачи при ламинарном законе Дарси примут вид:
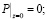
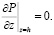(5)
Второе граничное условие относится к глубине h, ниже которой фильтрации не происходит. Величина порового давления P(z,t) при t=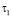
будет равна
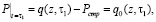(6)
т.е. часть нагрузки, равная величине структурной прочности сжатия Pстр [1], сразу же воспринимается скелетом грунта.
Уравнение консолидации водонасыщенных грунтов без учета их ползучести, согласно [8] примем в виде:
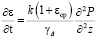, (7)
где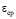 
– средний коэффициент пористости; 
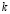– коэффициент фильтрации, γв – объемный вес воды; 
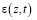– коэффициент пористости для исследуемого момента времени t и глубины z.
Если грунт деформируется только в вертикальном направлении, то по теории фильтрационной консолидации, сумма избыточного порового давления P(z,t) и эффективного напряжения в грунте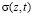 
в любой момент времени равно внешней нагрузке, т.е.
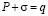. (8)
Исследование совместно выражений (1), (7), (8) приводит к следующему уравнению консолидации упругоползучих двухфазных грунтов:
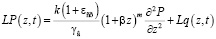, (9)
где 
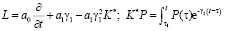d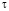
.
Таким образом, математическая постановка данной задачи сводится к следующему: требуется определить давление в поровой жидкости P(z,t), напряжение в скелете грунта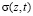 
и вертикальные перемещения верхней поверхности S(t) (осадок) уплотняемого грунтового основания. Для этого необходимо решить краевую задачу (9), (5), (6). Такие задачи в различных постановках рассмотрены в работах [2, 9]
Решение уравнения (9), удовлетворяющее начальному (6) и граничным (5) условиям представим в виде:
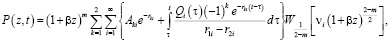(10)
где m 
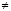2;
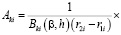
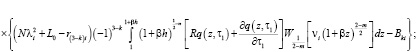
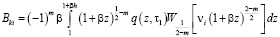. (11)
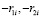– являются корнями квадратного уравнения вида
; 
; 
.
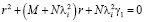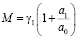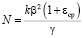Функции
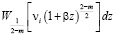
в зависимости от значений индекса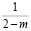 
находятся из следующих выражений:
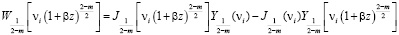(12)
при целом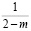 
,
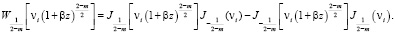(13)
при дробном индексе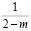 
. Здесь 
, 
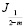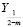– функции Бесселя соответственно первого и второго родов. Причем параметр n, входящий в (10)-(13) находится из следующих трансцендентных уравнений: для целого индекса 
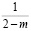из выражения
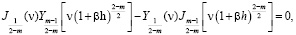(14)
для дробного индекса из
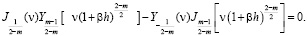(15)
Уравнения (14)-(15) при конкретных числах m имеют бесчисленные множества вещественных корней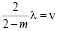 
.
Выражение (10) при (11)-(15) определяет значения порового давления в неоднородном упругоползучем грунте для любого момента времени. Его значение в момент времени, сколь угодно близкий к моменту приложения нагрузки, находится выражением
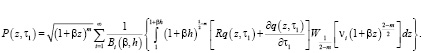
Оно зависит от соотношения проницаемости, уплотняемости и скорости нарастания ползучих деформаций грунта.
Напряжение в скелете грунта вычисляется по формуле
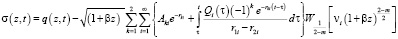. (16)
Если к поверхности слоя грунта приложена некая вертикальная нагрузка q(z,t), то соответствующая ей осадки S(t) может быть определены по формуле [8], т.е.
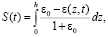(17)
где h – мощность уплотняемого неоднородного грунтового массива. Подынтегральное выражение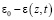 
находится из соотношения (1).
Рассмотрим уплотнение слоя неоднородного упругоползучего грунта под действием равномерно распределенной нагрузки с интенсивностью q. Тогда неконсолидированная осадка слоя неоднородного грунта (17), обладающего упругоползучим свойством имеет вид:
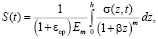(18)
Учитывая выражение напряжений для этого случая, равенство (18) приводим к виду:
S (t) =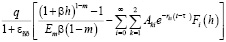 
, (19)
где
;
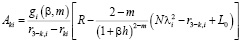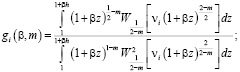
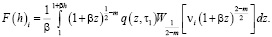(20)
При значений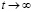 
из выражений (19), находим
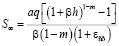. (21)
Здесь при значений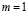 
в (21) образуется неопределенность типа 
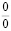, от неё можно избавится известным приемом математического анализа. Имея в виду выражения (20) и (21), степень консолидации грунта для любого момента времени вычисляется по формуле:
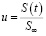, (22)
т.е.
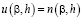
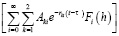, (23)
где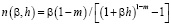 
,
Так как в основном при расчетах интересует всех значение порового давления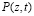 
в течение длительного промежутка времени после начало фильтрационной консолидации (более одного года), то учитывая быстро убывающий характер экспоненциальной функции 
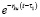при больших значениях показателя, то достаточно ограничиваться только первым членом ряда (10).
В качестве примера в данной работе исследована одномерная задача консолидации упругоползучего и непрерывно неоднородного по глубине грунта, модуль деформации и мера ползучести, которого изменяется с глубиной по законам:
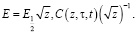
Для этого случая вычислены значения давлений поровой жидкости, напряжений в скелете грунта, осадки слоя и степень консолидации уплотняемого грунтового массива. Причем необходимо заметить, что учет переменности модуля деформации уплотняемого грунта существенно влияет качественно и количественно на эти величины. Задачи в других постановках исследованы в [3-5].
Библиографическая ссылка
Дасибеков А., Юнусов А.А., Юнусова А.А., Султанбек Т.С., Ханходжаева Г.Ш. ЗАДАЧА КОНСОЛИДАЦИИ НЕОДНОРОДНЫХ УПРУГОПОЛЗУЧИХ ГРУНТОВЫХ ОСНОВАНИЙ ПРИ УСТРОЙСТВЕ ПЕСЧАНОЙ ПОДУШКИ // Успехи современного естествознания. – 2014. – № 12-4. – С. 400-404;URL: https://natural-sciences.ru/ru/article/view?id=34620 (дата обращения: 09.12.2023).