На вопрос о механизме распространения запаха практически любQой преподаватель учебного заведения ( да и не только) ответит, что, конечно, это же диффузия. Однако ответ на этот вопрос не является таким очевидным.
Прежде всего, следует сослаться на публикацию в приложении к журналу «Квант» [1]. Там при решении задачи о механизме распространении запах в воздухе говорится о распространении запаха за счет конвекции, но в качестве альтернативы рассмотрено и влияние диффузии на этот процесс.
Попытаемся более подробно разобраться в этом вопросе. Первое, что надо сделать, это построить модель процесса распространения запаха. Начнем с диффузии в газах. ДИФФУЗИЯ (от лат. diffusio – распространение – растекание, рассеивание), движение частиц среды, приводящее к переносу вещества и выравниванию концентраций или к установлению равновесного распределения концентраций частиц данного сорта в среде.
В 1920 году Штерн ставит опыты по определению скоростей теплового движения молекул в опытах с молекулярными пучками. Эти опыты дали для наивероятнейшей скорости молекул серебра значения около 500 м/с. Совершенно ясно, что молекулы в газе не перемещаются поступательно именно с такой скоростью. Внутри вещества находится колоссальное количество молекул. Из основного уравнения МКТ
P = nkT
следует, что концентрация молекул газа равна
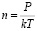 .
.
Рассчитаем концентрацию при нормальном атмосферном давлении и температуре 273 К.
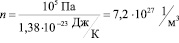 .
.
Нам невозможно представить себе такое число. Это невообразимо огромная величина, в земных условиях нет такого количества счетных величин. Расстояние, на которое перемещается молекула между двумя последовательными столкновениями, называется ее длиной свободного пробега. В силу хаотичности движения прямолинейные участки траектории, по которой движется молекула, могут сильно различаться по своей длине. Поэтому говорят о средней длине свободного пробега. Длина свободного пробега обратно пропорциональна квадратному корню из концентрации молекул.
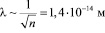 .
.
В воздухе школьного класса при нормальной плотности в течение 1 с молекула испытывает около 1 млрд. столкновений. При этом она постоянно меняет направление своего движения. Как же рассчитать теоретически время поступательного перемещения молекулы в одном направлении?
В какой-то мере диффузию можно уподобить броуновскому движению. Конечно, размер атомов гораздо меньше размера броуновских частиц, но нам кажется, что это не является принципиальным препятствием к проведению некоторых численных оценок.
Броуновское движение молекул подтверждает хаотический характер теплового движения и зависимость интенсивности этого движения от температуры. Впервые беспорядочное движение мелких твердых частиц, наблюдал английский ботаник Р. Броун в 1827 году, рассматривая взвешенные в воде твердые частички – споры плауна. С тех пор, движение частиц в жидкости или газе называется броуновским.
Теория броуновского движения в реальной жизни
Теория случайных блужданий имеет важное практическое приложение. Говорят, что в отсутствие ориентиров (солнце, звезды, шум шоссе или железной дороги и т.п.) человек бродит в лесу, по полю в буране или в густом тумане кругами, все время возвращаясь на прежнее место. На самом деле он ходит не кругами, а примерно так, как движутся молекулы или броуновские частицы. На прежнее место он вернуться может, но только случайно. А вот свой путь он пересекает много раз. Рассказывают также, что замерзших в пургу людей находили «в каком-нибудь километре» от ближайшего жилья или дороги, однако на самом деле у человека не было никаких шансов пройти этот километр, и вот почему.
Чтобы рассчитать, насколько сместится человек в результате случайных блужданий, надо знать величину λ, т.е. расстояние, которое человек может пройти по прямой, не имея никаких ориентиров. Эту величину с помощью студентов-добровольцев измерил доктор геолого-минералогических наук Б.С. Горобец. Он, конечно, не оставлял их в дремучем лесу или на заснеженном поле, все было проще – студента ставили в центре пустого стадиона, завязывали ему глаза и просили в полной тишине (чтобы исключить ориентирование по звукам) пройти до конца футбольного поля. Оказалось, что в среднем студент проходил по прямой всего лишь около 20 метров (отклонение от идеальной прямой не превышало 5°), а потом начинал все более отклоняться от первоначального направления. В конце концов, он останавливался, далеко не дойдя до края.
Пусть теперь человек идет (вернее, блуждает) в лесу со скоростью 2 километра в час (для дороги это очень медленно, но для густого леса – очень быстро), тогда если величина λ равна 20 метрам, то за час он пройдет 2 км, но сместится всего лишь на 200 м, за два часа – примерно на 280 м, за три часа – 350 м, за 4 часа – 400 м и т. д. Двигаясь по прямой с такой же скоростью, человек за 4 часа прошел бы 8 километров.
Далее следует вспомнить работы А. Эйнштейна и М. Смолуховского [2]. Именно они для броуновского движения получили выражение для среднеквадратичного смещения частицы вдоль произвольного направления:
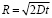 ,
,
здесь 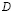 – коэффициент диффузии, t – время движения частицы. Зная коэффициент диффузии в газах D, и, задавая расстояние R, можно оценить время прохождения частицей этого расстояния.
– коэффициент диффузии, t – время движения частицы. Зная коэффициент диффузии в газах D, и, задавая расстояние R, можно оценить время прохождения частицей этого расстояния.
Если для коэффициента диффузии паров спирта в воздухе взять величину D=10-5 м2/с, для расстояния R=1 м, то получим время t ~ 5⋅104 с = 13,9 ч. Это достаточно красноречивый результат.
С другой стороны, нельзя ли рассматривать распространение запаха в условиях нарушения равновесности состояния среды (например, при наличии градиента концентрации)? Ведь согласно уравнения состояния идеального газа (1), и при наличии градиента концентрации в изотермической среде появляется градиент давления, который может привести к появлению конвекционных гидродинамических потоков внутри отдельных областей газа. В этом случае уже приходится говорить о конвекции, как основном механизме распространения запаха. Например, в условиях тепловой конвекции видно, что дым от сигарет достаточно быстро распространяется во все стороны, а не только вверх, под действием силы Архимеда, или вниз под действием силы тяжести. Правда, в этом случае речь идет о тепловой конвекции.
Перенос вещества, обусловленный одновременно молекулярной диффузией и макроскопическим движением среды (конвекцией), называется конвективной диффузией.
Конвективная диффузия может быть вызвана как действием на систему разности давлений, так и гравитационным полем. Если идет речь о сигаретном дыме, то мы имеем дело с конвективной диффузией, вызванной действием силы тяжести. В нашем случае при распространении запаха мы, вероятнее всего, имеем дело с конвективной диффузией, вызванной разностью давлений в различных частях среды. Механизм этого процесса достаточно сложен и выходит за рамки школьного курса физики.
Во второй части нашей статьи мы рассмотрим эксперимент, который был поставлен для выяснения роли конвективной диффузии в распространении запаха.
Библиографическая ссылка
Монастырский Л.М., Бондарев Р.В. К ВОПРОСУ О МЕХАНИЗМЕ РАСПРОСТРАНЕНИЯ ЗАПАХА В ВОЗДУХЕ. ЧАСТЬ 1 // Успехи современного естествознания. 2014. № 12-4. С. 448-450;URL: https://natural-sciences.ru/ru/article/view?id=34632 (дата обращения: 06.03.2026).



