Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бубин М.Н. 1

---

1 Юргинский технологический институт филиал ФГАОУ ВО «Национальный исследовательский Томский политехнический университет»

В статье идет речь о прогнозировании летне-осенних паводков при помощи аналитического метода изучения временных рядов – сингулярном спектральном анализе «ССА Гусеница». В работе представлено его описание, приведены результаты исследования реки Урал протекающей на территории Челябинской области. Применение сингулярного спектрального анализа позволяет прогнозировать высокие летне-осенние паводки на реках, тем самым заблаговременно предвидеть последствия наводнений.

Статья в формате PDF

2484 KB

летне-осенние паводки

временной ряд

сингулярный спектральный анализ

прогнозирование

наводнение

1. Анализ и прогноз временных рядов / Метод «Гусеница» [Электронный ресурс]. – Режим доступа: http://www.gistatgroup.com/gus/ (дата обращения 13.12.2014).

2. Главные компоненты временных рядов: метод «Гусеница» / под ред. Д.Л. Данилова. – Спб.: Пресском, 1997. – 308 с.

3. Голяндина Н.Э. Метод «Гусеница» SSA: анализ временных рядов. – Спб.: Спб ун-т, 2004. – 74 с.

4. Кашкин В.Б., Рублева Т.В. Применение сингулярного спектрального анализа для выделения слабо выраженных трендов // Известия Томского политехнического университета. – 2007. Т. 311. №5. – С. 116–119.

5. Управление риском трансграничных наводнений: опыт региона ЕЭК ООН. – Нью-Йорк и Женева: Издание Организации Объединенных Наций. – 2009. – 102 с.

Высокие летне-осенние паводки, проявляющиеся на реках, могут нанести серьезный ущерб промышленным объектам, населенным пунктам, сельскохозяйственным угодьям. Поэтому их прогнозирование является сложной многоуровневой задачей, актуальность которой обусловлена современным состоянием хозяйственных систем. Это в первую очередь касается урбанизированных и промышленных регионов, каким является Челябинская область. Наличие заблаговременной и достаточно точной прогнозной информации позволяет рационально спланировать и провести профилактические мероприятия по недопущению или минимизации ущерба от разлива рек. Поэтому исследования прогнозирования летне-осеннего стока является важной и актуальной задачей современной гидрологии.

При построении прогноза очень важно и актуально выбрать соответствующий метод исследования. В гидрологии большое распространение получили различные способы прогнозирования: графоаналитические, водно-балансовые, математического моделирования и др.

Методы гидрологических прогнозов максимального стока, разрабатывались и совершенствовались: Георгиевским Ю.М., Евстигнеевым В.М., Калининым Г.П., Рождественским А.В., Поповым Е.Г., Соколовым А.А. и др. Продолжением исследований явилось создание комплексных систем, прогнозирования наводнений и определения риска затопления территории. Среди прогнозных систем, в мировой практике, следует выделить: Систему предупреждения о наводнениях (Flood Warning System – FWS), Европейскую систему прогнозирования наводнений (European Flood Forecasting System, EFFS), Европейскую систему предупреждения о наводнениях (European Flood Alert System, EFAS) [5] и др. В России получили распространение различные программные проекты, основанные на математических прогнозных моделях режима рек с применением автоматизированных систем сбора гидрологической информации, где ключевыми моментами являются гидрометеорологические наблюдения в режиме реального времени. Но существует проблема разработки и применения единого программно-информационного комплекса, основанного на автоматических функциях прогнозирования гидрологического режима, с развитой системой принятия решений и оповещения, для предотвращения ущерба хозяйственных объектов. Данный вопрос в настоящее время остается не решенным.

Одной из версий построения прогнозных моделей летне-осеннего стока может служить сингулярный спектральный анализ, реализуемый электронной компьютерной программой «Caterpillar SSA». Данный способ является очень удобным приемом для сжатия информации, ее сглаживания и прогнозирования. В дальнейшем он может использоваться в качестве основы для построения гидрологических программных продуктов прогнозирования наводнений.

Разработка метода приходится на 60-е годы ХХ в., когда он был обоснован сотрудниками Санкт-Петербургского государственного университета [2, 3]. Главная цель его появления – исследование колебаний и прогнозирование. Также метод независимо разрабатывался в Великобритании и США, там он получил название – Singular Spectrum Analysis (SSA) и стал применяться при исследовании временных рядов наблюдений различных совокупностей.

В качестве характеристики метода следует отметить, его возможность анализировать последовательность временных рядов, его алгоритм, позволяет легко вычленять из ряда главные компоненты. Способ обладает возможностью не учитывать возмущающие колебания не гидрологического характера, сгладить исходные данные, заполнить пропуски и сделать прогноз ряда. К тому же метод «ССА Гусеница» приспособлен для работы в среде Windows, что позволяет быстро проводить аналитические расчеты [1].

Базовый вариант метода подразумевает преобразование одномерного временного ряда длиной n с равномерным шагом (x1, x2, x3,...xn) в многомерный при помощи однопараметрической сдвиговой процедуры исследования полученной многомерной траектории с помощью анализа главных компонент и восстановления ряда по выбранным компонентам. Базовый алгоритм метода «ССА Гусеница» можно разбить на четыре этапа [4].

Этап №1 состоит из развертки одномерного ряда в многомерный – из исходного ряда составляется матрица Х:

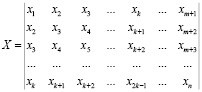. (1)

В матрице m < n – длина гусеницы, последней строкой с номером k=n+m-1 являются элементы (xk, xk+1,...xn), причем xij=xi+j–1. Эту матрицу можно представить как m-мерную выборку объема k или m-мерный временной ряд.

Этап № 2, включает анализ главных компонент – вычисляются собственные числа, сингулярное разложение выборочной корреляционной матрицы. Рассчитываются средние значения μi по столбцам, матрица Х центрируется. Далее вычисляется матрица R=(1/k)х*хT. Если матрица X центрирована, то R является выборочной корреляционной матрицей:

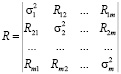. (2)

Элементами матрицы R служат выражения:

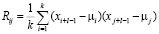. (3)

По обычной методике анализа главных компонент вычисляются собственные числа и собственные векторы матрицы R, т.е. производится ее сингулярное разложение.

Этап № 3, отбор главных компонент. Процедура « ССА Гусеница» порождает набор линейных фильтров настроенных на составляющие исходного процесса. При этом собственные векторы матрицы выступают в роли переходных функций соответствующих фильтров. Выделение спектральных компонентов ряда осуществляется линейным преобразованием исходного процесса с помощью дискретного оператора свертки:

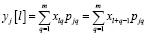. (4)

Выбор нескольких главных компонент подобен параллельному соединению нескольких фильтров. Ширина полосы пропускания фильтра определяется видом собственного вектора и длинной интервала усреднения (длиной «гусеницы» m). Ширина полосы пропускания обратно пропорциональна m. Максимальное значение m равно половине длины ряда n, в этом случае при четном n матрица X квадратная. При небольших m, вплоть до m=2, происходит сглаживание ряда. Вид собственных векторов и главных компонент, полученных в результате фильтрации, дает информацию о структуре изучаемого процесса и свойствах его слагаемых. Среди главных компонентов можно наблюдать те, что относятся к тренду (медленно меняющихся), ритмических, шумовых.

Этап № 4, восстановление одномерного ряда путем вставки промежуточных интерполированных значений между исходными значениями. Данная процедура основана на разложении матрицы ряда Х и восстановлении по набору главных компонент. В результате получаются приближенные значения матрицы ряда или части этой матрицы. Переход к исходному ряду формально может быть осуществлен усреднением матрицы ряда по побочным диагоналям и может привести к некоторому искажению полученной структуры.

Сингулярный спектральный анализ «ССА Гусеница» можно использовать для прогнозирования высоких летне-осенних паводков на реках Челябинской области, на основе выборки данных по расходам стока за этот период. В качестве примера, представлен прогноз паводков на р. Урал – Кизильское до 2020 года (рисунок).

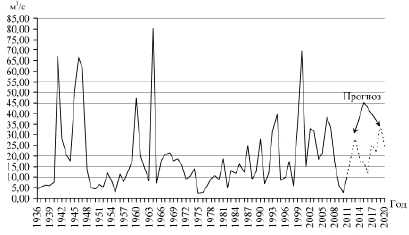
Прогнозирование летне-осенних паводков на р. Урал – Кизильское с помощью сингулярного спектрального анализа «ССА Гусеница»

Для подтверждения достоверности гидрологического ряда наблюдений за летне-осенним стоком, рассчитывалась относительная среднеквадратическая ошибка среднего многолетнего значения, которая составила 9,15 %. Также для проверки прогноза применялся Фурье-анализ. Расчеты показали, что на р. Урал – Кизильское, существует 6-летний ведущий гидрологический ритм (таблица), который наблюдался на рисунке.

Проявление ведущего 6-летнего ритма многолетних колебаний летне-осеннего стока р. Урал – Кизильское

Изучение летне-осенних паводков сингулярным спектральным анализом позволяет демонстративно строить прогнозы, тем самым заблаговременно предвидеть последствия наводнений. Следует заметить, что все проводимые расчеты являются теоретическими. Методов, которые в реальности рассчитывают долгосрочные прогнозные количественные характеристики летне-осеннего стока пока не существует, тем более что наблюдается тенденция изменения климата. Поиск таких способов продолжается в настоящее время, что представляет большую и сложную задачу современной гидрологии.

Библиографическая ссылка