О некоторых проблемах достоверности результатов численного моделирования нестационарных упругих волн напряжений
В настоящее время активно применяются численные методы для решения различных задач нестационарной механики деформируемого твердого тела. Однако при решении сложных задач возникают проблемы оценки достоверности полученных результатов. На основании изложенного можно утверждать, что оценка точности и достоверности результатов численного моделирования волн напряжений в областях сложной формы является актуальной фундаментальной и прикладной научной задачей.
Некоторая информация о физической достоверности и математической точности моделирования волн напряжений в деформируемых областях с помощью разработанного численного метода, алгоритма и комплекса программ приведена в следующих работах [1–4, 10].
О постановке задачи и реализация численного метода, алгоритма и комплекса программ
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями – используем метод конечных элементов в перемещениях. Задача решается методом сквозного счета, без выделения разрывов. На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных динамических воздействиях на сложные системы. При разработке комплекса программ использовался алгоритмический язык Фортран-90. Исследуемая область разбивается по пространственным переменным на треугольные и прямоугольные конечные элементы первого порядка. По временной переменной исследуемая область разбивается на линейные конечные элементы первого порядка.
Некоторые вопросы в области постановки, разработки методики, алгоритма, комплекса программ и результатах решенных нестационарных динамических задач рассмотрены в следующих работах [1–10].
О моделировании нестационарных упругих волн в пластинке
1. Рассмотрим задачу об отражении упругих волн напряжений в виде дельта функции от свободной поверхности. На границе пластинки AB (рис. 1) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/∆t) изменяется линейно от 0 до P, а при n ≥ 10 от P до 0 (P = σ0, σ0 = – 0,1 МПа).
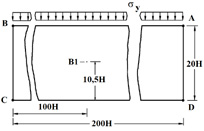
Рис. 1. Постановка задачи об отражении волн напряжений
Граничные условия для контуров ВС и АВ при t > 0 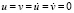 . Контур CD свободен от нагрузок. Отраженные волны от контуров ВС и АD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 2 представлено изменение нормального напряжения
. Контур CD свободен от нагрузок. Отраженные волны от контуров ВС и АD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 2 представлено изменение нормального напряжения 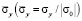 во времени n в точке B1.
во времени n в точке B1.
2. Рассмотрим задачу об отражении упругих волн напряжений в виде функции Хевисайда от свободной поверхности.
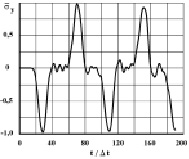
Рис. 2. Изменение упругого нормального напряжения 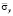 во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде дельта функции от свободной поверхности
во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде дельта функции от свободной поверхности
На границе пластинки AB (рис. 1) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/∆t) изменяется линейно от 0 до P, а при n ≥ 10 равно P (P = σ0, σ0 = – 0,1 МПа). Граничные условия для контуров BC и AD при t > 0 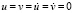 . Контур CD свободен от нагрузок. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 3 представлено изменение нормального напряжения
. Контур CD свободен от нагрузок. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 3 представлено изменение нормального напряжения 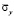 (
(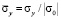 ) во времени n в точке B1.
) во времени n в точке B1.
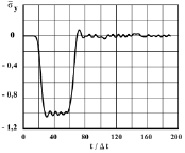
Рис. 3. Изменение нормального напряжения 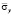 во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде функции Хевисайда от свободной поверхности
во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде функции Хевисайда от свободной поверхности
3. Рассмотрим задачу об отражении упругих волн напряжений в виде дельта функции от жесткой поверхности.
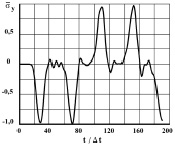
Рис. 4. Изменение нормального напряжения 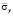 во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде дельта функции от жесткой поверхности
во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде дельта функции от жесткой поверхности
На границе пластинки AB (рис. 1) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/∆t) изменяется линейно от 0 до P, а при n ≥ 10 от P до 0 (P = σ0, σ0 = – 0,1 МПа). Граничные условия для контуров BC, AD и CD при t > 0 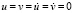 . Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 4 представлено изменение нормального напряжения
. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 4 представлено изменение нормального напряжения 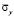 (
(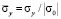 ) во времени n в точке B1.
) во времени n в точке B1.
4. Рассмотрим задачу об отражении упругих волн напряжений в виде функции Хевисайда от жесткой поверхности.
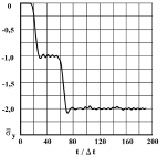
Рис. 5. Изменение нормального напряжения 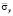 во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде функции Хевисайда от жесткой поверхности
во времени n в точке B1 в задаче об отражении упругих волн напряжений в виде функции Хевисайда от жесткой поверхности
На границе пластинки AB (рис. 1) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/∆t) изменяется линейно от 0 до P, а при n ≥ 10 равно P (P = σ0, σ0 = – 0,1 МПа). Граничные условия для контуров BC, AD и CD при t > 0 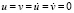 . Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 5 представлено изменение нормального напряжения
. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 5 представлено изменение нормального напряжения 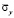 (
(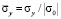 ) во времени n в точках B1.
) во времени n в точках B1.
5. Рассмотрим задачу об интерференции плоских продольных упругих волн напряжений в виде дельта функции. На границе пластинки AB (рис. 6) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/∆t) изменяется линейно от 0 до P, а при n ≥ 10 от P до 0 (P = σ0, σ0 = – 0,1 МПа). На границе пластинки CD (рис. 6) приложено нормальное напряжение σy, которое при 0 ≤ n 10 изменяется линейно от 0 до P, а при n ≥ 10 от P до 0 (P = σ0, σ0 = 0,1 МПа). Граничные условия для контуров BC и AD при t > 0 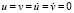 . Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 7 представлено изменение нормального напряжения
. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 7 представлено изменение нормального напряжения 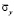 (
(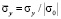 ) во времени n в точках B1.
) во времени n в точках B1.
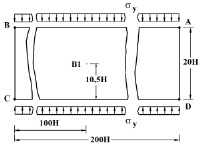
Рис. 6. Постановка задачи об интерференции волн напряжений
6. Рассмотрим задачу об интерференции плоских продольных упругих волн напряжений в виде функции Хевисайда.
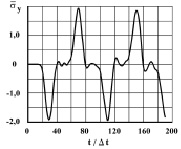
Рис. 7. Изменение нормального напряжения 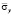 во времени n в точке B1 в задаче об интерференции плоских продольных упругих волн напряжений в виде дельта функции
во времени n в точке B1 в задаче об интерференции плоских продольных упругих волн напряжений в виде дельта функции
На границе пластинки AB (рис. 6) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 (n = t/∆t) изменяется линейно от 0 до P, а при n ≥ 10 равно P (P = σ0, σ0 = – 0,1 МПа). На границе пластинки CD (рис. 6) приложено нормальное напряжение σy, которое при 0 ≤ n ≤ 10 изменяется линейно от 0 до P, а при n ≥ 10 равно P (P = σ0, σ0 = – 0,1 МПа). Граничные условия для контуров BC и AD при t > 0 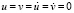 . Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 8 представлено изменение нормального напряжения
. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 8 представлено изменение нормального напряжения 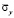 (
(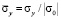 ) во времени n в точках B1.
) во времени n в точках B1.
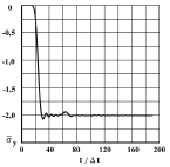
Рис. 8. Изменение нормального напряжения 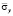 во времени n в точке B1 в задаче об интерференции плоских продольных упругих волн напряжений в виде функции Хевисайда
во времени n в точке B1 в задаче об интерференции плоских продольных упругих волн напряжений в виде функции Хевисайда
Выводы
1. Сравнение с результатами отражения и интерференции волн напряжений показало хорошее совпадение, что позволяет сделать вывод о физической достоверности и математической точности результатов численного решения динамических задач, полученных методом конечных элементов в перемещениях.
2. Методика, алгоритм, комплекс программ и результаты решенных задач рекомендуются для использования в научно-технических организациях, специализирующихся в области динамического расчета сооружений с окружающей средой при ударных, взрывных и сейсмических воздействиях.
Библиографическая ссылка
Мусаев В.К. ОЦЕНКА ТОЧНОСТИ И ДОСТОВЕРНОСТИ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ЗАДАЧ ОБ ОТРАЖЕНИИ И ИНТЕРФЕРЕНЦИИ НЕСТАЦИОНАРНЫХ УПРУГИХ ВОЛН НАПРЯЖЕНИЙ // Успехи современного естествознания. 2015. № 1-7. С. 1184-1187;URL: https://natural-sciences.ru/ru/article/view?id=35035 (дата обращения: 03.03.2026).



