Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Розыходжаева Г.А. 1 Игнатьев Н.А. 2 Усманова З.А. 3

---

1 Центральная клиническая больница № 1

2 Национальный университет Узбекистана имени Мирзо Улугбека

3 Ташкентский институт усовершенствования врачей

Рассмотрены вопросы, связанные с разработкой информационной модели нестабильности атеросклеротической бляшки с учетом активности матриксных металлопротеаз и их ингибиторов. Подробно освещены все этапы интеллектуального анализа данных проведенного исследования. Разработана логическая модель нестабильной атеросклеротической бляшки. Получено решающее правило, согласно которому вычислялось значение индекса нестабильности атеросклеротической бляшки.

Статья в формате PDF

280 KB

информационная модель

матриксная металлопротеиназа-9

тканевой ингибитор металлопротеиназы-1

нестабильная атеросклеротическая бляшка

1. Игнатьев Н.А. Интеллектуальный анализ данных на базе непараметрических методов классификации и разделения выборок объектов поверхностями. – Ташкент: Национальный университет Узбекистана им. Мирзо Улугбека, 2008. – 108 с.

2. Игнатьев Н.А., Нуржонов Ш.Ю. Выбор параметров регуляризации для повышения обобщающей способности дискриминантных функций // Узбекистон Республикаси Курол Кучлари академиясининг хабарлари. – 2014. – № 1 (14). – C. 81–87.

3. Игнатьев Н.А. Извлечение явных знаний из разнотипных данных с помощью нейронных сетей // Вычислит. технологии. – 2003. – № 2 (8). – С. 69–73.

4. Игнатьев Н.А. О повышении эффективности реализации методов итеративной группировки // Проблемы управления и информатики. – 2002. – № 1. – С. 115–119.

5. Игнатьев Н.А., Мадрахимов Ш.Ф. О некоторых способах повышения прозрачности нейронных сетей // Вычислит. технологии. – 2003. – № 6 (8). – С. 31–37.

6. Колесникова С.И. Методы анализа информативности разнотипных признаков // Вестник Томского государственного университета Управление, вычислительная техника и информатика. – 2009. – № 1 (6). – C. 69–80.

7. Пальцева Е.М. Комплексный подход к молекулярной диагностике ряда социально значимых заболеваний: автореф. дис. … д-ра мед. наук. – М.: МГУ, 2010. – 47 с.

8. Патент Российская Федерация № 2385668. Способ индивидуальной количественной оценки риска развития клинических проявлений атеросклероза / Бовтюшко В.Г., Бовтюшко П.В., Поддубский Г.А., Юсупов А.Н. // Бюл. – 2010. – № 10.

9. Полонская Я.В., Чернявский A.M., Волков А.М. и др. Корреляции биомаркеров воспаления и деструкции в крови и в сосудистой стенке у мужчин с коронарным атеросклерозом // Бюллетень СО РАМН. – 2011. – № 5. – С. 25–30.

10. Розыходжаева Г.А. Функциональное состояние сердечно-сосудистой системы больных ишемической болезнью сердца пожилого и старческого возраста (патогенетические и клинико-диагностические аспекты): автореф. дис. … д-ра мед. наук. – Ташкент: РСНПМЦТ и МР, 2006. – 44 с.

11. Юсупов А.Н., Бовтюшко П.В. Применение искусственных нейронных сетей в оценке риска развития клинических проявлений атеросклероза // Вестник Российской Военно-медицинской академии. Приложение. – 2010. – № 2 (30) – С. 193–197.

12. Юсупов А.Н. Применение искусственных нейронных сетей в оценке риска развития клинических проявлений атеросклероза у работников, занятых во вредных условиях труда (на примере нефтеперерабатывающих производств): автореф. дис. … канд. биол. наук. – М.: ФГБУ «Военно-медицинская Академия имени С.М. Кирова», 2012. – 24 с.

13. Fiotti N., Altamura N., Orlando C. et al. Metalloproteinases-2, -9 and TIMP-1 expression in stable and unstable coronary plaques undergoing PCI // Int. J. Cardiol. – 2008. – Vol. 21. – Р. 350–357.

Ранняя диагностика различных заболеваний на основе биологических маркеров в последние годы становится более актуальной [7, 9]. В кардиологии большой интерес вызывает выявление в крови биомаркеров, характеризующих состояние атеросклеротической бляшки (АСБ). В последнее время широко обсуждается роль матриксных металлопротеиназ (ММП) и их тканевых ингибиторов (ТИМП) в патогенезе нестабильности АСБ [13]. Анализ современных литературных источников показал, что необходимы дальнейшие исследования, чтобы понять роль ММП и ТИМП, вовлеченных в атерогенез и разрыв бляшки. Настоящая работа выполнена в соответствии с приоритетными направлениями развития науки и технологии Республики Узбекистан в рамках программы ГНТП-9 «Разработка новых технологий профилактики, диагностики, лечения и реабилитации заболеваний человека» в рамках прикладного Государственного научно-технического проекта МЗ РУз АДСС 25 «Разработка метода ранней прижизненной диагностики атеросклероза магистральных артерий».

Цель исследования – разработка информационной модели нестабильности атеросклеротической бляшки с учетом активности матриксных металлопротеаз и их тканевых ингибиторов.

Материалы и методы исследования

Работа по интеллектуальному анализу медицинских данных по атеросклеротическим бляшкам проводилась совместно с сотрудниками кафедры программных и сетевых технологий Национального университета Узбекистана имени М. Улугбека.

По данным клинических, лабораторных, инструментальных исследований сформирована обучающая выборка, которая послужила основой при построении информационной модели для решения задач прогнозирования. Для решения задач математического моделирования с использованием обобщенных оценок мы отобрали данные 73 больных ИБС со стенозом сонной артерии более 50 %. Основным условием включения в анализируемую базу данных было отсутствие пропусков в вариационном ряде. В базу данных введено 83 параметра. В работе использовались обобщённые оценки – агрегированные (комбинированные) показатели, которые применялись для отображения отношений между объектами двух групп (классов K1, K2) в разнотипном признаковом пространстве на числовую ось. В K1, K2 включены соответственно пациенты со стабильными и нестабильными АСБ более 50 % по результатам предварительного дуплексного сканирования. Для получения комбинированных показателей использовано правило агломеративной иерархической группировки разнотипных признаков с целью нелинейного отображения их значений в описании объектов на числовую ось.

Результаты исследования и их обсуждение

Анализ данных проведенного исследования включал следующие этапы:

1. Разведочный анализ с учетом пропусков (не измеренных значений) в данных.

2. Формирование набора информативных признаков на основе оценки их вкладов в процесс разделения классов.

3. Формирование обучающей выборки путём удаления шумовых объектов.

4. Отбор индивидуальных информативных наборов признаков для каждого объекта.

5. Нелинейное отображение определяемых наборов признаков на числовую ось и формирование решающего правила.

Для разработки информационной модели использовано 9 методов обследования, 83 параметра (признака), 73 из которых измерялись в количественных и 10 в номинальной шкалах измерений.

Использование традиционных методов статистики (например, метода Стьюдента) допускает включение в анализ только количественных признаков. Методы статистики не позволяют оценить значимость качественных показателей и сочетаний количественных и качественных показателей в принятии решений. Статистические характеристики количественных признаков по классам K₁, K₂ приведены в таблице.

Статистические характеристики количественных признаков по стабильным и нестабильным АСБ

Учитывая сложность постановки диагноза в многопараметрическом пространстве, предлагается в качестве инструментария при формировании математической модели диагностирования пациентов со стабильной и нестабильной АСБ применить технологию синтеза обобщенных оценок. Обобщённые оценки – это агрегированные (комбинированные) показатели, которые используются для отображения отношений между объектами двух групп (классов K₁, K₂) в разнотипном признаковом пространстве на числовую ось [1].

Комбинированные показатели формируют новое признаковое пространство, размерность которого меньше исходного. Для получения комбинированных показателей использовано правило агломеративной иерархической группировки разнотипных признаков с целью нелинейного отображения их значений в описании объектов на числовую ось. Результаты нелинейного отображения рассматривались как значения обобщённых оценок (новых признаков) в описании объектов.

При решении задач прогнозирования АСБ применялся метод поиска логических закономерностей в форме нелинейных проекций обобщённых оценок объектов по определяемым наборам из 31-го признака (симптома, синдрома) на выборке из представителей классов K₁ и K₂. В самую устойчивую закономерность вошли 5 исходных показателей: вес пациента, ТИМП-1, ММП-9, ФВ, СССА. Согласно решающему правилу с пороговым значением [2] вычислялось значение индекса нестабильности атеросклеротической бляшки (ИНАСБ):

ИНАСБ = 0,2∙(0,99623∙(y3 – 0,02887) – – 0,0061∙(СССА – 55,0)) + 0,8∙(9,1088603533E – 03)∙(y3∙СССА + 1,41804) – 0,0125,

где

y₁ = 0,3∙(–0,00059∙(ММП-9 – 274,96) – 0,0003∙(ТИМП-1 – 1602,878)) + + 0,7∙(–2,6440737712E – 07)∙(ММП-9∙ТИМП-1 – 428481,41184);

y₂ = 0,2∙(1,00483∙(y1 + 0,01192) – 0,0091∙(ФВ % – 60,0)) + + 0,8∙(1,5979164850E – 02)∙(y1∙ФВ % + 0,77465);

y₃ = 0,6∙(0,00448∙(вес – 72,0) + 1,06∙(y2 + 0,00913)) + + 0,4∙(1,0333362905E – 02)∙(вес∙y2 + 0,72105).

Если ИНАСБ > 0, то пациент относится к классу стабильной АСБ, при ИНАСБ < 0 – к классу нестабильной АСБ. Пороговое значение для решающего правила из [2] вычислялось по формуле

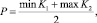
где min K₁, max K₂ – сответственно минимальное значение обобщённой оценки из класса K₁ и максимальное из K₂ [3].

Математический аппарат интеллектуального анализа данных является наиболее приемлемой альтернативой традиционному статистическому анализу, так как позволяет избежать искажения результатов оценки риска развития клинических проявлений атеросклероза в случаях введения в систему новых данных, появления данных, существенно отличающихся от основной массы наблюдений, и ошибочных измерений [10, 12]. Для извлечения новых знаний (скрытых закономерностей) из базы данных мы использовали современные методы интеллектуального анализа [6].

В отличие от традиционных статистических методов интеллектуальный анализ находит широкое применение там, где необходимо моделировать подобие человеческой интуиции и, как правило, трудно построить явные алгоритмы. Для достижения высокой точности решения прикладных задач данные должны соответствовать набору жестких требований. Из теории и практики вычислений известно, что эти требования часто бывают диаметрально противоположными. Алгоритмы методов интеллектуального анализа могут использоваться в качестве инструментария для пополнения баз знаний экспертных систем [1].

Опыт использования системы диагностики доклинического атеросклероза подтвердил эффективность применения медицинской статусметрии в целях своевременной профилактики сердечно-сосудистых заболеваний атерогенной природы. Однако одновременно был выявлен и ряд серьезных недостатков используемой системы, проявляющихся в значительном искажении оценки риска для лиц, показатели которых имели значения, далеко отстоящие от основной массы наблюдений [8].

В другом исследовании [11, 12] искусственные нейронные сети (ИНС) рассматривались в качестве математического аппарата, воспроизводящего условную функцию частоты на основании альтернативных обучающих выборок. Математический аппарат ИНС приведен как наиболее приемлемая альтернатива модели Фишера для оценки риска развития атеросклероза по данным врачебных, инструментальных и лабораторных исследований.

В отличие от перечисленных выше исследований применение метода вычисления обобщенных оценок с помощью иерархической агломеративной группировки в нашей работе было целесообразным по следующим причинам [1]:

– обобщённые оценки образуют новое признаковое пространство, размеры которого меньше исходного;

– решается проблема использования алгоритмов классификации, реализация которых была неэффективна из-за большой размерности признакового пространства, либо возможна при одном типе шкал измерений;

– в процессе группировки происходит последовательный отбор информативных наборов признаков;

– нелинейное отображение описаний объектов на числовую ось по определяемым комбинациям признаков является средством обнаружения устойчивых логических закономерностей (новых знаний) в хранилищах данных [2].

Нелинейное отображение описаний объектов на числовую ось по определяемым комбинациям признаков является средством обнаружения устойчивых логических закономерностей (новых знаний) в хранилищах данных [1, 2, 3, 4, 5]. Статистические методы для этих целей не подходят, так как в процессе вычисления статистических показателей используются усредненные данные.

В работе решалась задача повышения информативности и устойчивости прогнозирования нестабильности АСБ у пациентов с каротидным атеросклерозом за счет вычисления индекса нестабильности атеросклеротической бляшки. Существующие методы прогнозирования (например, способ индивидуальной количественной оценки риска развития клинических проявлений атеросклероза [8]) имеют основной недостаток – большое число исследуемых параметров показателей, полученных в ходе клинического обследования, которые попадают в область равенства прогностических коэффициентов.

В данном исследовании поставленная задача решается с применением решающего правила в форме нелинейных зависимостей между такими пятью исходными показателями как вес пациента, ТИМП-1, ММП-9, ФВ, СССА. Эти исходные показатели образуют латентный (явно не измеряемый) признак. Смысл полученного результата заключается в повышении информативности и устойчивости оценки риска развития нестабильной АСБ и индивидуального риска развития клинических осложнений АСБ. В самую устойчивую закономерность вошли пять исходных показателей: вес пациента, ТИМП-1, ММП-9, ФВ, СССА. Используя данные предварительного обследования и значений этих пяти показателей (вес пациента, ТИМП-1, ММП-9, ФВ, СССА), которые прямо или косвенно отражают интенсивность развития атеросклеротических процессов на всех стадиях развития, в клинической практике возможно с высокой эффективностью прогнозировать нестабильность атеросклеротической бляшки. Данные верификации разработанной модели диагностики атеросклеротического процесса показали в 92 % случаев соответствие диагнозам пациентов, полученным по экспертной информации.

Высокая чувствительность метода к изменению взаимосвязей показателей позволяет спрогнозировать развитие нестабильности АСБ, провести своевременные профилактические и лечебные мероприятия. Последующий анализ динамики риска позволяет также оценить эффективность принятых мер и при необходимости скорректировать профилактику и лечение клинического атеросклероза.

Выводы

1. Разработанный алгоритм автоматизированной диагностики с использованием математических методов способствует повышению информативности и устойчивости прогнозирования нестабильности АСБ у пациентов с каротидным атеросклерозом за счет вычисления индекса нестабильности атеросклеротической бляшки.

2. Выделенные на основе информационного подхода наиболее существенные «веcомые» факторы, вошедшие в наиболее устойчивую закономерность (вес пациента, сывороточный уровень ТИМП-1, ММП-9, фракция выброса левого желудочка по данным эхокардиографии и степень стеноза сонных артерий по данным дуплексного сканирования) позволяют оптимизировать лечебно-диагностический процесс при атеросклерозе. Получено решающее правило, согласно которому на основе вышеуказанных факторов можно вычислить значение индекса нестабильности атеросклеротической бляшки.

3. Разработанная логическая модель НАСБ направлена на повышение достоверности результатов диагностики. Данные верификации разработанной модели диагностики атеросклеротического процесса показали в 92 % случаев соответствие диагнозам пациентов, полученным по экспертной информации.

Библиографическая ссылка