Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Хисматуллин А.С. 1, 2 Вахитов А.Х. 2 Феоктистов А.А. 2

---

1 Государственное автономное научное учреждение «Институт прикладных исследований Республики Башкортостан»

2 Филиал «Уфимский государственный нефтяной технический университет»

Настоящая статья посвящена интенсификации процесса теплообмена, который заключается в том, что теплосъем с нагревающегося масла в трансформаторе осуществляется за счёт циркуляции барботируемого элегаза, перекачиваемого компрессором. После всплытия пузырьков элегаз проходит через систему фильтров, удерживающих частицы масла, захваченные всплывающими пузырьками, и далее, пройдя систему очистки и охлаждения, повторяет рабочий цикл. В работе рассмотрены явления теплопереноса, инициированные акустическим полем в среде. Показано, что значения коэффициентов переноса возрастают даже в случае распространения плоской волны в однородной среде. Полученное спектральное представление позволяет построить выражение коэффициентов трансцилляторного переноса, обусловленного колебаниями для различных волновых пакетов. Результаты исследований показывают, что при пропускании элегазовых пузырьков через трансформаторное масло происходит возрастание коэффициента эффективной теплопроводности. Предлагаемый метод интенсификации системы охлаждения за счёт увеличения коэффициента переноса тепла в масле позволяет повысить эффективность системы охлаждения силовых масляных трансформаторов.

Статья в формате PDF

2773 KB

трансцилляторный перенос тепла

монохроматическая волна

число маха

акустические поля

1. Баширов М.Г., Хисматуллин А.С., Хуснутдинова И.Г. Применение барботажа в системе охлаждения силовых трансформаторов / Транспорт и хранение нефтепродуктов и углеводородного сырья. – 2014. – № 3. – С. 29–33.

2. Баширов М.Г., Хисматуллин А.С., Салиева Л.М., Зайнакова И.Ф. Совершенствование хроматографического метода оценки технического состояния силовых масляных трансформаторов / Фундаментальные исследования. – 2015. – № 10 (часть 2). – С. 233–237.

3. Баширов М.Г., Хисматуллин А.С., Камалов А.Р. Исследование изменения теплопроводности масла при барботаже в системе охлаждения силовых трансформаторов // Современные проблемы науки и образования. – 2014. – № 6. – С. 338.

4. Муллакаев М.С. Ультразвуковая интенсификация технологических процессов добычи и переработки нефти, очистки нефтезагрязненных вод и грунтов. Дис. докт. техн. наук. Московский государственный университет инженерной экологии. – М.: 2011. – 391 с.

5. Филиппов А.И., Минлибаев М.Р., Хисматуллин А.С. Установка для исследования коэффициента температуропроводности в жидкости // Новые промышленные технологии. – 2010. – № 2. – С. 62-63.

6. Хисматуллин А.С., Гареев И.М. Исследование переноса интегрального параметра в жидкости с газовыми пузырьками // Экологические системы и приборы. – 2015. – № 7. – С. 38–42.

7. Хисматуллин А.С. Расчет теплового поля в силовых масляных трансформаторах с элегазовым охлаждением / Транспорт и хранение нефтепродуктов и углеводородного сырья. – 2015. – № 2. – С. 23–30.

8. Хисматуллин А.С., Камалов А.Р. Повышение эффективности системы охлаждения мощных силовых трансформаторов // Фундаментальные исследования. – 2015. – № 6–2. – С. 316–319.

9. Хисматуллин А.С., Минлибаев М.Р., Аллагулов А.И. Контроль и управление технологическими параметрами системы охлаждения масляного трансформатора / Повышение надежности и энергоэффективности электротехнических систем и комплексов: межвузовский сборник научных трудов // редкол.: В.А. Шабанов и др.– Уфа: Изд-во УГНТУ, 2014. – С. 121–123.

10. Хисматуллин А.С. Теоретическое и экспериментальное исследование теплопереноса в жидкости с газовыми пузырьками: дис. на соискание уч. ст. канд. физ.-мат. наук. – Уфа, 2010. – С. 14–16.

11. Хисматуллин А.С., Филиппов А.И., Минлибаев М.Р., Серебренников Н.П. Определение коэффициента трансцилляторного переноса при барботаже в жидкости // Вестник Воронежского государственного технического университета. – 2010. – № 2. – С. 52–53.

12. Bashirov M.G., Minlibayev M.R., Hismatullin A.S. Increase of efficiency of cooling of the power oil transformers. Oil and Gas Business: electronic scientific journal. – 2014. – Issue 2. – Р. 358–367.

13. Nigmatulin R.I., Filippov A.I., and Khismatullin A.S. Transcillatory heat transfer in a liquid with gas bubbles // Thermophysics and Aeromechanics. – 2012. – Vol. 19, № 4. – Р. 589.

14. Хисматуллин А.C., Филиппов А.И. Исследование явлений переноса в жидкости с газовыми пузырьками при акустическом воздействии // Обозрение прикладной и промышленной математики. – М., 2008. – Т. 15, № 1. – С. 179–180.

15. Хисматуллин А.С., Баширов М.Г., Исхаков Р.Р. Свидетельство о государственной регистрации программ для ЭВМ № 2015614073 Программа анализа выходных данных эксперимента по определения коэффициента температуропроводности трансформаторного масла с всплывающими элегазовыми пузырьками. Правообладатель: ФГБОУ ВПО УГНТУ. Дата гос. регистрации 06.04.2015.

В работе исследуются процессы теплопереноса в промышленных силовых трансформаторах, основанных на барботировании трансформаторного масла пузырьками элегаза. Большое значение коэффициента теплового расширения элегаза способствует образованию конвективных потоков, перераспределяющих неоднородности теплового поля в объеме трансформаторного масла [4–6]. В среде с конвективными ячейками возникает сложное поле скоростей, которое приводит к возрастанию эффективного коэффициента теплопроводности. При определенных условиях величина эффективного коэффициента теплопроводности может на несколько порядков превышать молекулярный коэффициент теплопроводности, поэтому исследование механизма переноса тепла в объеме трансформаторного масла с конвективными ячейками имеет важное практическое значение для повышения эффективности системы охлаждения силовых трансформаторов [7–15].

В работе также рассмотрены явления теплопереноса, инициированные акустическим полем в среде. Магнитопровод трансформатора является основным и важным источником шума. Шум сердечника зависит от магнитных свойств материала, из которого он изготовлен, и от плотности магнитного потока. Магнитные силы, формируемые в сердечнике, вызывают вибрацию и шум. Шумы, вызываемые сердечником и обмотками, находятся, в основном, в полосе частот 100–600 Hz. Частотный диапазон шума, вызванного вентиляторами охлаждения, как правило, имеет более широкий диапазон частот. Факторами, влияющими на общий шум вентиляторов, являются скорость вращения, структура лопастей, количество вентиляторов и расположение радиаторов.

Экспериментально установлено [1], что при воздействии волновых полей в сложных средах возрастают значения коэффициентов переноса. Физический механизм этого явления, достаточно сложен, и до настоящего времени нет полной теории этого явления. Одним из механизмов, объясняющих явление возрастания коэффициентов переноса, является так называемый трансцилляторный [2–7]. Суть этого механизма проявляется в увеличении потока за счет относительного смещения участков среды, вызываемого волновыми полями. Трансцилляторный теплоперенос относится к диффузионно-конвективным процессам, возникающим при колебательном относительном перемещении участков или частей среды [5]. Теория явления трансцилляторного переноса приводит к уравнениям в частных производных второго порядка с переменными коэффициентами.

Рассмотрим простейший случай однородной среды, находящейся под воздействием плоской монохроматической или немонохроматической волны. Уравнение, описывающее эволюцию температуры T в однородной изотропной среде, представляется в виде

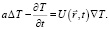(1)

Оно учитывает диффузионные и конвективные процессы, возникающие за счет смещений в волновой зоне. Здесь а – диффузный коэффициент, 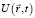– поле скоростей в волновой зоне.

Получение аналитических решений уравнения (1) для волновых полей затруднено вследствие сложной зависимости скорости колебаний от координат и времени [1]. Решим задачу методом редукции к эквивалентному интегральному уравнению, не требующий построения точного аналитического решения. Для простоты предположим, что волна является поперечной и распространяется вдоль оси Ox со скоростью υ, а отличной от нуля является координата скорости колебаний среды Uy(x, t). Начальное температурное предполагается заданным 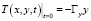. Считаем также, что составляющая градиента скалярного поля Гy является постоянной. Построение математической модели при этих предположениях сводится к отысканию решений вида

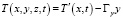. (2)

Рассмотрим случай монохроматической волны с частотой ω. Для плоской упругой поперечной волны, распространяющейся вдоль оси Ox, с плоскостью колебаний, параллельной оси Oy, имеем

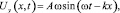
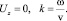(3)

Для соответствующего уравнения относительно T’(x, t)

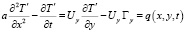, (4)

где q(x, y, t) – эквивалентный источник тепла, с однородным начальным условием

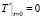. (5)

Эквивалентное исходной задаче интегро-дифференциальное уравнение с учетом того, что Гy >> ∂T’/∂y и используя формулы Эйлера, получим:

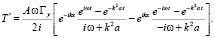(6)

Для достаточно больших времен 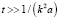из (6) получим

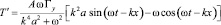. (7)

Поток вдоль оси Oy складывается из диффузионного и конвективного:

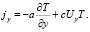(8)

Осредненная конвективная составляющая потока по периоду колебаний для потока имеет следующий вид:

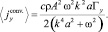(9)

Соответствующий коэффициент переноса

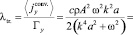
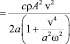(10)

называется трансцилляторным. Трансцилляторный перенос возникает за счет диффузного обмена между слоями среды, участвующими в колебательном относительном перемещении. Он отличается от чисто конвективного, поскольку регулярного переноса среды в этом случае нет.

Разложим (10) в степенной ряд и, удерживая два члена, получим

,

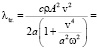
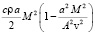где 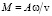– число Маха.

Рассмотрим далее случай плоской немонохроматической волны, бегущей вдоль оси Oy. Представив соответствующую координату скорости смещения среды в виде интеграла Фурье, получим выражение для нахождения коэффициента трансцилляторного переноса в волновой зоне.

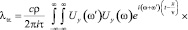
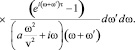(11)

Практическое значение этой формулы заключается в возможности вычисления коэффициента переноса, если известны спектральные компоненты поля скорости в волновой зоне. Для произвольных периодических колебаний представим поле скорости в виде экспоненциального ряда:

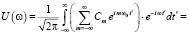
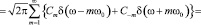
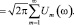(12)

Для заданных коэффициентов Фурье смещений Am и Bm в волновом поле имеем следующее выражение для КТП:

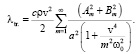(13)

Полученное выражение свидетельствует об аддитивности КТП относительно гармоник Фурье. Для монохроматических колебаний A1 = A и Am = 0 при m ≠ 1, Bm = 0 из (13) получим выражение, совпадающее с (10). Следовательно, это позволяет констатировать, что коэффициент трансцилляторного переноса пропорционален квадрату амплитуды колебаний. При увеличении частоты ω0 коэффициент монотонно возрастает, стремясь к предельному значению .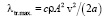

Таким образом, при распространении поперечной акустической волны в среде возникает дополнительный перенос тепла (трансцилляторный). Коэффициент теплопроводности получает максимальное приращение в плоскости колебаний. Изотропная среда в акустическом поле приобретает анизотропию по отношению к коэффициентам переноса. Трансцилляторный перенос обуславливает дополнительную необратимость процессов переноса.

С целью проверки полученных теоретических расчетов были проведены экспериментальные исследования на разработанном лабораторном стенде.

Лабораторный стенд состоит из реактора, нагревательного элемента, микрокомпрессора, измерительных устройств, сопряженных с компьютером. В качестве реактора использована ёмкость радиусом 12,5 см и высотой 30 см, заполненная трансформаторным маслом, на оси которого по центру закреплен нагревательный элемент. Газовые пузырьки создаются с помощью микрокомпрессора, осуществляющего впрыск газа через специальные керамические распределители, расположенные в нижней части реактора. Регулирование интенсивности нагрева трансформаторного масла происходило с помощью лабораторного автотрансформатора, подключённого к нагревательному элементу. Для регистрации температурного поля в объеме емкости размещены термопары, сигналы с которых поступают на вход аналогово-цифрового преобразователя ADAM4018. Далее сигналы направляются в компьютер, который позволяет управлять, регистрировать и обрабатывать информацию, с помощью специально разработанной программы [15].

Выводы

Результаты исследований показали, что при пропускании элегазовых пузырьков через трансформаторное масло коэффициент эффективной теплопроводности возрастает в 27 раз [13]. Фактически это означает, что при этом механизм трансцилляторного переноса тепла становится преобладающим.

Механизм теплообмена следующий: основной теплосъём с нагревающегося масла в трансформаторе осуществляется за счёт циркуляции барботируемого элегаза, обладающего большим коэффициентом теплового расширения, в масле образуется конвективный поток, эффективно уносящий тепло. После всплытия пузырьков, элегаз проходит через систему фильтров, удерживающих частицы масла, захваченные всплывающими пузырьками, и далее, пройдя систему очистки и охлаждения, возвращаются обратно в работу для повторения рабочего цикла. Предложенный способ интенсификации системы охлаждения позволяет повысить эффективность системы охлаждения силовых трансформаторов за счёт барботирования масла элегазом, что значительно повышает коэффициент эффективной теплопроводности.

Библиографическая ссылка