Данная работа является естественным продолжением исследований специалистов КНЦ РАН по проблеме пыления хвостохранилищ на базе методов численного моделирования. В определенной мере информация, представленная в публикациях [3, 4, 6], является авторским взглядом на проблему интенсивности пыления на начало 2012 г.
Более глубокое «погружение» в проблему позволило авторам на основе анализа существующих подходов по оценке интенсивности пыления (пустыни, хвостохранилища и др.) существенно продвинуться в понимании как сопровождающих процесс пыления физических механизмов, так и их математического описания. Некоторые результаты выполненного исследования представлены в докладах на российских и международных конференциях [1, 2, 7].
В частности, были рассмотрены подходы по оценке интенсивности пыления, приемлемые для решения практических задач по исследованию влияния скорости ветрового потока на уровень интенсивности пыления хвостохранилища АНОФ-2, а значит, и на загрязнение атмосферы для района г. Апатиты при северо-западном ветре. По результатам анализа сделан предварительный вывод, что наиболее приемлемыми для последующих исследований загрязнения приземного слоя атмосферы вниз по ветровому потоку могут быть признаны зависимость D.L. Westphal et al. [9] и схема DEAD [8]. Именно эти зависимости дают минимальное расхождение результатов на всем рассмотренном диапазоне скорости ветрового потока. Отметим, что оба подхода базируются на функциональной зависимости потока массы пыли от динамической скорости на высоте пыления в 4-й и 3-й степенях соответственно.
При рассмотрении турбулентного переноса пыли с хвостохранилища АНОФ-2 представляется разумным ограничиться частицами, размер которых не превышает 70 мкм.
Авторский подход к оценке динамической скорости
На рис. 1 представлена схема модели, которая принимается для обоснования величины скорости, необходимой для оценки вертикального потока массы частиц (интенсивности пыления). Основная идея − динамическая скорость на высоте пылящей поверхности u* определяется через осредненную горизонтальную компоненту референтной скорости ветра набегающего потока на высоте +10 м uref на основе численных расчетов для различной высоты пылящей дамбы.

Рис. 1. Схема модели под обоснование методики определения интенсивности пыления
На входной границе модели рассмотрим диапазон значений референтной скорости ветра uref на высоте 10 м над основанием модели (от 5 до 23 м/с, например, с шагом 3 м/с). Задавая логарифмический профиль скорости на входной границе области (шероховатость принимается на уровне 0,05 м), выполняем расчет аэродинамики на базе стационарной стандартной (k – ε)-модели турбулентности [3, 4, 6]. Далее выполняем обработку расчетных аэродинамических параметров вдоль пунктирной линии рис. 1: операцию осреднения горизонтальной компоненты скорости на высоте +10 м над пылящей поверхностью u10. Результаты обработки численных экспериментов для горизонтальной скорости на высоте +10 м над пылящей поверхностью, а также переход к динамической скорости u* обобщены в табл. 1.
Дополнительно для последующего использования при численном решении уравнения конвективно-диффузионного переноса пыли выполнено осреднение (по области моделирования) значений коэффициентов динамической турбулентной вязкости. Результаты этой операции приведены в табл. 1. Последующий переход к значениям коэффициентов турбулентной диффузии стандартен, ранее использован и описан авторами в работах [3, 4, 6].
Гранулометрический состав (в графической форме) отвальных хвостов с поверхности устоявшегося пляжа хвостохранилища АНОФ-2 приведен в диссертационной работе А.В. Стриженок [5]. Обработка информации позволила авторам получить количественные показатели по долям («вес» интервала) каждого моделируемого интервала размера частиц пыли (табл. 2). В табл. 2 также приведены значения пороговой скорости 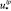 для пыли интервала крупности p до 70 мкм в диаметре с шагом 10 мкм, рассчитанные по методике авторов работы [8]), а также скорости оседания разнокалиберной пыли, вычисленные в Стоксовом приближении [3] и необходимые для последующих вычислений конвективно-диффузионного переноса.
для пыли интервала крупности p до 70 мкм в диаметре с шагом 10 мкм, рассчитанные по методике авторов работы [8]), а также скорости оседания разнокалиберной пыли, вычисленные в Стоксовом приближении [3] и необходимые для последующих вычислений конвективно-диффузионного переноса.
Таблица 1
Осредненные значения горизонтальной скорости на высоте +10 м u10, динамической скорости u* на высоте поверхности пыления и турбулентной динамической вязкости ηt
|
Скорость uref, м/с |
u*, м/с |
u10, м/с |
ηt, Па.с |
|
1 |
2 |
3 |
4 |
|
5 |
0,623 |
8,246 |
0,4086 |
|
8 |
0,996 |
13,19 |
0,6563 |
|
11 |
1,370 |
18,14 |
0,9053 |
|
14 |
1,743 |
23,09 |
1,1554 |
|
17 |
2,117 |
28,04 |
1,4067 |
|
20 |
2,490 |
32,98 |
1,6593 |
|
23 |
2,863 |
37,93 |
1,9136 |
Таблица 2
Значения «веса» интервала, пороговой скорости и скорости оседания в зависимости от срединного диаметра частиц пыли
|
Срединный диаметр (диапазон интервала), мкм |
«Вес» интервала, – |
Пороговая скорость |
Скорость оседания wg, м/с |
|
1 |
2 |
3 |
4 |
|
5 (0–10) D1 |
0,022 |
0,951 |
0,00195 |
|
15 (10–20) D2 |
0,083 |
0,420 |
0,0175 |
|
25 (20–30) D3 |
0,142 |
0,295 |
0,0487 |
|
35 (30–40) D4 |
0,194 |
0,243 |
0,0955 |
|
45 (40–50) D5 |
0,209 |
0,218 |
0,1580 |
|
55 (50–60) D6 |
0,189 |
0,206 |
0,2360 |
|
65 (60–70) D7 |
0,161 |
0,201 |
0,3290 |
а
б
в
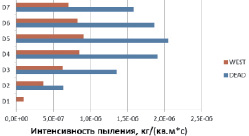
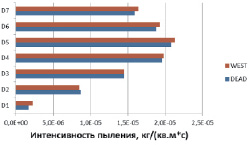
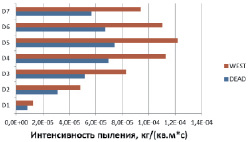
Рис. 2. Поинтервальные интенсивности пыления при вариации скорости ветра: а – 5 м/с; б – 11 м/с; в – 17 м/с
Анализ интенсивности пыления
Некоторые результаты вычислений поинтервальных вертикальных потоков массы для схемы DEAD [8] и зависимости D.L. Westphalet.al. [9] при вариации скорости ветра с использованием необходимых параметров, приведенных в табл. 1 и 2, представлены на рис. 2 ((а) 5 с, (б) 11 м/с и (в) 17 м/с).
Безусловно, яркой особенностью расчетных интенсивностей пыления, выполненных для схемы DEAD, является отсутствие числового значения при скорости ветра 5 м/с для самой мелкой пыли D1 (срединный диаметр 5 мкм). Данный факт имеет очевидное объяснение: величина пороговой скорости (табл. 2, 3-й столбец, 2-я строка) выше значения динамической скорости (табл. 1, 2-й столбец, 2-я строка), т.е. в рамках данной модели (схема DEAD) эмиссии пыли такой крупности не происходит.
Анализ показывает, что при малых скоростях ветрового потока (не более 8 м/с) практически для пыли любой крупности значения интенсивности пыления, рассчитанные по схеме DEAD (рис. 2, а), несколько выше аналогичных расчетных данных по зависимости D.L. Westphal et.al. При величине скорости ветрового потока 11 м/с результаты расчетов интенсивности пыления по обоим используемым подходам наиболее близки (рис. 2, б). Дальнейшее увеличение скорости ветра (встречается существенно реже) приводит к тому, что расчетные (по зависимости D.L. Westphal et.al.) интенсивности пыления заметно превышают аналогичные величины, вычисленные с использованием схемы DEAD (рис. 2, в).
Обобщением расчетных данных являются кривые рис. 3, а и б, на которых представлены суммарные интенсивности пыления при вариации либо скорости ветрового потока, либо расчетной величине динамической скорости на высоте пыления соответственно. Поведение кривых рис. 3, а и б подтверждают указанный выше факт: до величины скорости ветрового потока 11 м/с превалирует кривая интенсивности пыления по схеме DEAD, а при более высокой скорости − кривая по зависимости D.L. Westphal et.al. Пересечение кривых происходит вблизи отметки 11 м/с.
Построенные кривые описываются степенными функциями AVn в 4-й (зависимость D.L. Westphal et.al.) и 3-й (схема DEAD) степенях либо скорости ветрового потока, либо расчетной величине динамической скорости на высоте пыления. Коэффициенты пропорциональности A в степенных зависимостях следующие: для рис. 2, а: I – 8,031 и II – 6,987; для рис. 2, б: I – 3,877 и II – 2,896. Размерность скорости V в обоих случаях м/с.
Расчетные данные интенсивности пыления необходимы при решении конвективно-диффузионного уравнения распространения пыли при описании граничных условий на поверхности пыления. В силу того, что указанное уравнение является линейным, достаточно будет выполнить численные эксперименты по пространственно-временному распределению концентрации пыли в исследуемой области, например, для данных зависимости D.L. Westphal et.al.. Зная соответствующие отношения интенсивностей пыления, пересчитываем значения концентрации пыли, отвечающие эмиссии пылевых частиц по схеме DEAD. В результате прогноз пространственно-временного распределения концентрации пыли будет определяться в некотором диапазоне значений.
Естественно, авторы понимают, что для верификации численной модели необходимо проведение трудоемких экспериментальных исследований на объекте пыления, что, к сожалению, не может быть реализовано по целому ряду причин. Предпринята попытка проверить на объективность полученные значения интенсивности пыления. Для этого проанализированы данные отчета «Реконструкция хвостохранилища до отметки 200 м: проектная документация. Раздел 8 «Перечень мероприятий по охране окружающей среды», посвященного реконструкции хвостохранилища АНОФ-2 до высотной отметки 200 м. Специалисты ЗАО «Механобр Инжиниринг» используют показатель – «максимальная удельная сдуваемость пыли». В своих оценках авторы указанного отчета используют значение 5,29∙10–6 кг/(м2∙с), что в представленных на рис. 3, б графических зависимостях отвечает значению динамической скорости не выше 0,6 м/с.
Выводы
Проанализированы два подхода по оценке интенсивности пыления (зависимость D.L. Westphal et al. и схема DEAD), которые, по мнению авторов, наиболее приемлемы для решения практической задачи о влиянии скорости ветрового потока и высоты пылящей поверхности на загрязнение атмосферы (на примере хвостохранилища АНОФ-2). Оба подхода базируются на функциональной зависимости потока массы от динамической скорости на высоте пыления в 4-й и 3-й степенях соответственно.
Продемонстрирован достаточно простой и нетрудоемкий переход к определению динамической скорости u* и скорости на высоте +10 м над пылящей поверхностью u10 по данным референтной скорости ветра набегающего потока и высоты дамбы. Указанные величины, определяемые на базе созданной двухмерной численной модели аэродинамики атмосферы исследуемой области, позволяют осуществить оценки интенсивности пыления.
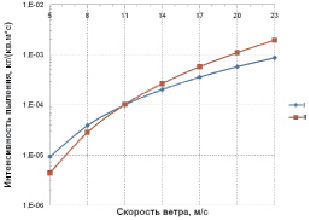
а
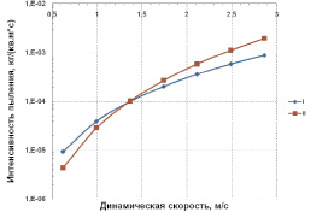
б
Рис. 3. Расчетные суммарные интенсивности пыления в зависимости: а – от скорости ветрового потока на референтной высоте; б – от динамической скорости на высоте пыления; I – схема DEAD (ромб); II – зависимость Westphal D.L. et.al. (квадрат)
Выполнен сравнительный анализ расчетных значений поинтервальной интенсивности пыления на базе выбранных подходов при вариации скорости ветрового потока в широком диапазоне. Указан экономичный путь дальнейших численных экспериментов по прогнозу пространственно-временного распределения поинтервальной концентрации пыли, основанный на линейной природе конвективно-диффузионного уравнения и выполненном анализе расчетных вертикальных потоков массы пыли с использованием зависимости D.L. Westphal et al. и схемы DEAD.
Библиографическая ссылка
Маслобоев В.А., Бакланов А.А., Амосов П.В. ЭФФЕКТ СКОРОСТИ ВЕТРОВОГО ПОТОКА НА ИНТЕНСИВНОСТЬ ПЫЛЕНИЯ ХВОСТОХРАНИЛИЩА // Успехи современного естествознания. 2016. № 3. С. 177-182;URL: https://natural-sciences.ru/ru/article/view?id=35845 (дата обращения: 07.03.2026).




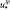 , м/с
, м/с