Обустройство нефтяных и газовых месторождений связано со строительством различных трубопроводов (газопроводы, нефтепроводы, водопроводы, теплопроводы) в мерзлых и вечномерзлых грунтах. При проектировании, строительстве и эксплуатации трубопроводов различного назначения следует учитывать то обстоятельство, что большую часть времени они находятся в зоне грунта с отрицательной температурой. Это может вызвать, с одной стороны, замерзание транспортируемой жидкости, а с другой – протаивание мерзлого грунта в основании трубопроводов и расположенных вблизи сооружений [1]. При глубоком сезонном промерзании грунтов (до 4,2 м) водопроводные и канализационные сети, в соответствии с действующими нормами, должны прокладываться в зоне глубокого заложения. Высокий уровень грунтовых вод значительно усложняет технологию производства работ и увеличивает их объем. Поэтому увеличение глубины заложения трубопроводов нежелательно и практически трудно выполнимо [4].
Для решения вышеизложенных затруднений были предложены несколько вариантов совмещенной прокладки сетей. При подземной прокладке в одной траншее совмещаются канал теплопровода, водопровод и канализация. Водопровод укладывается на уровне подошвы теплофикационного канала с одной стороны, а канализационные трубы – с другой.
На температурный режим грунтов существенное влияние оказывают подземные инженерные коммуникации и особенно – теплопроводы. Выяснение закономерностей формирования ореолов протаивания вокруг теплопроводов и определение оптимальных условий прокладки теплопроводов при строительстве в районах с вечномерзлыми грунтами на севере Тюменской области является весьма актуальной задачей [6, 8].
В обычной постановке процесс распространения теплоты в массиве описывается системой уравнений теплопроводности [2]. Рассматриваемая область делится на талую и мерзлую зоны, для которых записываются уравнения
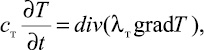(1)
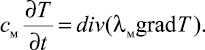(2)
Здесь T = T(x, t) – поле температур; c, λ – теплоемкость и коэффициент теплопроводности соответственно; индекс «м» относится к мерзлой, а «т» – к талой зоне.
На подвижной границе раздела фаз ξ(t), кроме неразрывности температуры, задается условие Стефана, связывающее скачок потоков теплоты на границе со скоростью его распространения
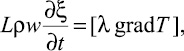(3)
где L – удельная скрытая теплота льдообразования; ρ – плотность породы; w – влажность. Здесь и далее для простоты рассматриваются одномерные задачи, так как в случае многомерных задач ни к идеологии моделирования, ни к математической технике ничего не добавляется. Точное аналитическое решение данной задачи возможно лишь иногда, например при неизменных теплофизических параметрах талого и мерзлого грунтов и в постоянных граничных условиях первого рода. Для реальных грунтов теплофизические параметры зависят от температуры, и уравнения (1)–(2) становятся нелинейными, поэтому аналитическое решение возможно только приближенно при некоторых допущениях [3, 5, 7].
Расчет температурного поля в грунте вокруг прямоугольного канала теплопроводов
Выбор оптимального варианта размещения инженерных коммуникаций в одной траншее в значительной степени определяется температурным режимом грунта вокруг канала теплопроводов.
Существующие методики рекомендуют производить расчет температурного поля грунта вокруг теплопроводов в канале по одной из модификаций формулы Форхгеймера [1, 2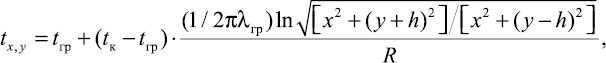, 4]
(4)
где tx, y – температура любой точки грунта, удаленной на величину x от вертикальной плоскости, проходящей через ось канала, и на величину y – от поверхности грунта, 0С; tгр – естественная температура грунта на глубине оси канала, 0С; tк – температура воздуха в канале, 0С; λгр – теплопроводность грунта, Вт/(м·K); h – глубина заложения оси канала от поверхности земли, м; R – суммарное тепловое сопротивление внутренней поверхности канала, стенок и грунта, определяемое по формуле
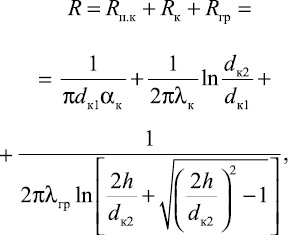(5)
где αк – коэффициент теплообмена от воздуха внутри канала к стенкам канала, Вт/(м2·K); λк – теплопроводность стенок железобетонного канала; dк1, dк2 – эквивалентные диаметры канала соответственно внутренний и наружный.
C целью анализа температурного режима сезоннопромерзающего грунта были построены графики температурных полей вокруг канала теплопроводов по различным методикам и проведено их сравнение с экспериментальными данными, полученными в тождественных условиях. Установлено, что температурный режим грунта вокруг прямоугольных каналов теплопроводов в реальных условиях значительно отличается от полученного расчетным путем по формуле (4).
Для проверки соответствия того или иного теоретически рассчитанного температурного поля действительному распределению температур вокруг канала в грунте сравнивали идентичные поля (рис. 1 и 2). Сравнение показало, что кривые распределения температур в грунте, определенные по формуле (4) и приведенные на рис. 1, не соответствуют фактически замеренным на экспериментальных участках (рис. 2).
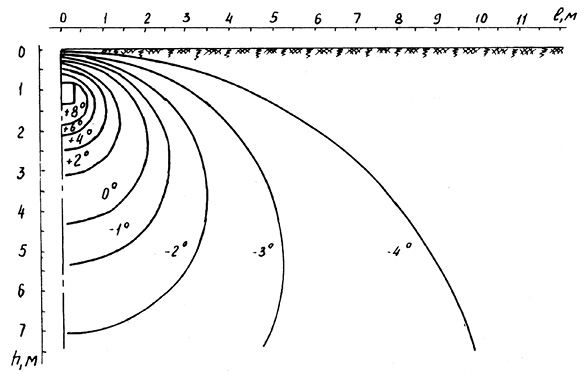
Рис. 1. Температурное поле грунта вокруг канала теплопроводов, определенное по модифицированной формуле Форхгеймера
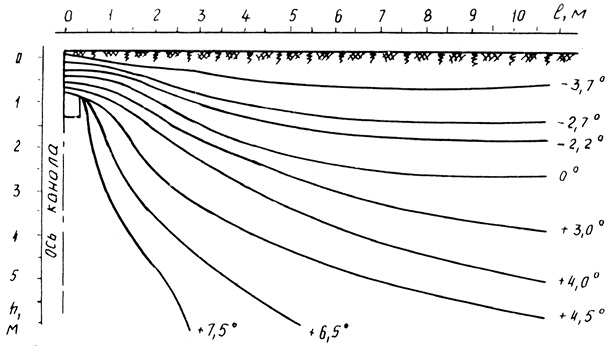
Рис. 2. Осредненное температурное поле грунта вокруг канала теплопроводов (по данным натурных наблюдений)
Проведены также расчеты температурного поля вокруг канала теплопроводов по методу суперпозиции для суммирования температурного поля, создаваемого самим каналом теплопроводов, и естественно температурного поля грунта. Для сравнения температурных полей вокруг канала теплопроводов, полученных расчетным путем с применением принципа суперпозиции, с полями, наблюдавшимися в экспериментальных условиях, были выполнены расчеты по их определению. Суммировали два температурных поля, образованных действием двух различных по виду тепловых источников. Первое – от канала теплопроводов при нулевой температуре окружающего грунтового массива; второе – обусловленное только температурным градиентом грунта и зависящее от сезонных колебаний температуры воздуха на поверхности. Суммирование первого и второго полей дает результирующее поле вокруг канала теплопроводов. Разнородные (мерзлую и талую) зоны приводили к единой среде с приведенными теплопроводностью λпр и температурой tпр.
Температурные поля, образованные тепловым влиянием только самого канала теплопроводов, строились по формуле
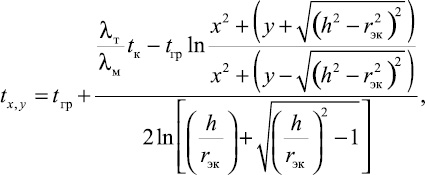(6)
где tгр – температура грунта, принимаемая в расчетах равной нулевой температуре, 0С; λг, λм – теплопроводность соответственно талой и мерзлой зоны, Вт/(м·K); rэк – радиус эквивалентного по теплопотерям канала, равный P/2π (P – периметр прямоугольного канала), м.
Термическое сопротивление на границе «воздух – стенка» 1/αк, а если необходимо, то и собственное сопротивление стенки канала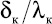 
может быть выражено через величину эквивалентного грунтового слоя, прибавляемую в формуле (6) к глубине заложения центра канала h.
Данные для построения температурных полей по формуле (6) и естественного температурного поля грунта, зависящего от сезонных колебаний температуры воздуха на поверхности, получены при натурных наблюдениях. В результате суммирования собственного температурного поля от канала теплопроводов и естественного поля грунта было получено результирующее поле (рис. 3). Сопоставление температурных полей позволило установить, что температурное поле вокруг канала теплопроводов можно представлять с достаточной для практических расчетов степенью точности в виде суммы двух полей – температурного, образованного тепловым влиянием самого канала теплопроводов и определенного по формуле (6) при нулевой температуре окружающего грунтового массива, а также естественного температурного поля грунта, зависящего от сезонных колебаний температуры наружного воздуха. Таким образом, метод суперпозиции и замены нестационарных тепловых состояний рядом последовательных установившихся состояний при тепловом расчете для магистральных нефтепроводов применим и для прямоугольных каналов теплопроводов [1, 6].
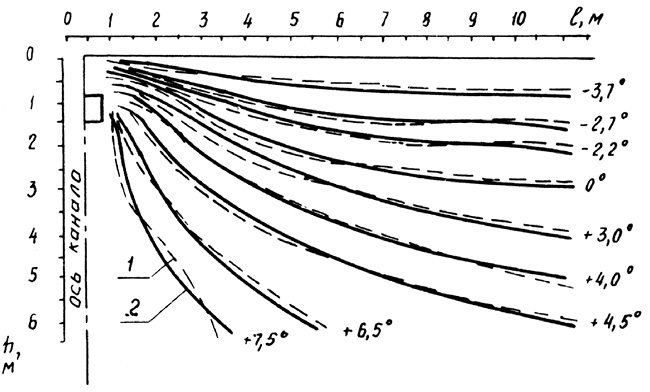
Рис. 3. Результирующее температурное поле грунта вокруг канала теплопроводов, полученное: 1 – по экспериментальным данным (пунктирные линии); 2 – по результатам расчета (сплошные линии)
Расчет талой зоны вокруг канала теплопроводов
Для определения оптимального варианта прокладки инженерных коммуникаций и обоснования возможности размещения водопроводных и канализационных сетей в зоне теплового влияния теплотрассы большое значение имеет знание зоны талого грунта вокруг канала теплопроводов. Величина талой зоны вокруг канала теплотрассы в горизонтальном направлении (считая от оси канала на уровне его подошвы) может быть определена из следующего выражения, полученного в результате эксперимента на гидроинтеграторе и обработки экспериментальных данных методом обобщенных переменных [1, 6, 9].
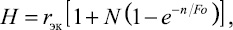(7)
где rэк – эквивалентный радиус канала по теплопотерям, равный P/2π (P – периметр прямоугольного канала), м;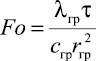 
– критерий Фурье; λг – теплопроводность грунта, Вт/(м·K); τ – время, ч; сгр – теплоемкость грунта, кДж/(м3·K).
Коэффициенты N и n являются функциями от Bi, Kо и tк/t0. Для их определения получены следующие зависимости:
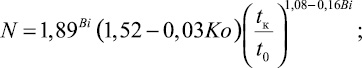(8)
n = 0,07•1,4–Bi, (9)
где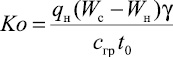 
– критерий Коссовича; 
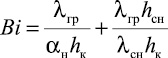– модифицированный критерий Био; qп – удельная теплота плавления льда, принимаемая равной 365 кДж/кг; Wc – суммарная влажность грунта, доли единицы; t0 – температура грунта на глубине нулевых годовых амплитуд, 0С; αн – коэффициент теплообмена на дневной поверхности, Вт/(м2·K); Wн – весовое содержание незамерзающей воды, доли единиц; γ – объемный вес скелета грунта, кг/м3; hн – заглубление канала теплотрассы до верха плиты, м; hcн – высота снежного покрова, м; λcн – теплопроводность снега, Вт/(м·K).
Изменения критериев были установлены с учетом природных условий Среднего Приобья в достаточно широком диапазоне:
3 ≤ tк/t0 ≤ 9; 2,4 ≤ Ko ≤ 12;
0 ≤ Fo ≤ 6280; 0,1 ≤ Bi ≤ 4,1. (10)
В целях максимального упрощения и облегчения расчетов по формулам (7)–(9) составлена обобщенная расчетная номограмма (рис. 4), позволяющая легко рассчитывать величину талой зоны грунта вокруг канала теплотрассы. Ниже приводится пример расчета по предложенной методике.
Пример
Требуется определить величину талой зоны вокруг канала теплотрассы в сезоннопромерзающем грунте за 15 лет эксплуатации при следующих исходных данных. Теплопроводы проложены в непроходном железобетонном канале марки КЛ-90-45, с внутренним сечением 0,90×0,45 м. Трубы стальные бесшовные с диаметром 108×3,5 мм, изолированные минеральным войлоком толщиной 40 мм. По изоляции предусматривается покровный слой асбестоцементной штукатурки толщиной 15 мм. Параметры теплоносителя: температура воды в подающем трубопроводе равна 130 0С и в обратном – 70 0С. Среднегодовая температура воздуха tк в непроходных железобетонных каналах при заглублении их от поверхности грунта до верха плиты на 0,8 м принимается на основании наблюдений и расчетов. Для данных условий tк = 30 0С.
Грунт – суглинок с суммарной влажностью, равной 0,334, с содержанием незамерзшей воды – 0,1 (в долях единицы). Объемный вес скелета грунта равен 1500 кг/м3. Заглубление канала от поверхности грунта до верха плиты составляет 0,8 м. Температура грунта на глубине нулевых годовых амплитуд – 5 0С. Теплопроводность грунта – 1,8 Вт/(м·K). Объемная теплоемкость грунта – 2100 кДж/(м3·K). Удельная теплота плавления льда – 335 кДж/кг. Среднезимняя высота снежного покрова – 0,1 м, его теплопроводность – 0,30 Вт/(м·K). Коэффициент теплообмена на дневной поверхности равен 15 Вт/(м2·K).
Решение
Согласно исходным данным, определяют следующие параметры:
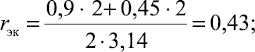
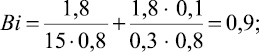
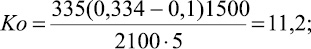
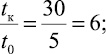
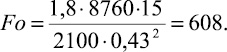
Для сравнения найдем величину талой зоны по формулам (7)–(9) и по номограмме (рис. 4).
Получаем
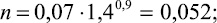
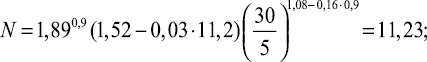
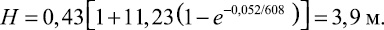
Пользуясь номограммой при найденных Ko, Bi, Fo, определяем H/rэк. Ход решения показан на номограмме. На шкале Ko находим точку с отметкой 11,2. Из этой точки проводим вертикаль до пересечения с лучом Bi = 0,9. Затем из данной точки проводим горизонталь до пересечения с кривой tк/t0 = 6. Из полученной точки проводим вертикаль до «немой» шкалы.
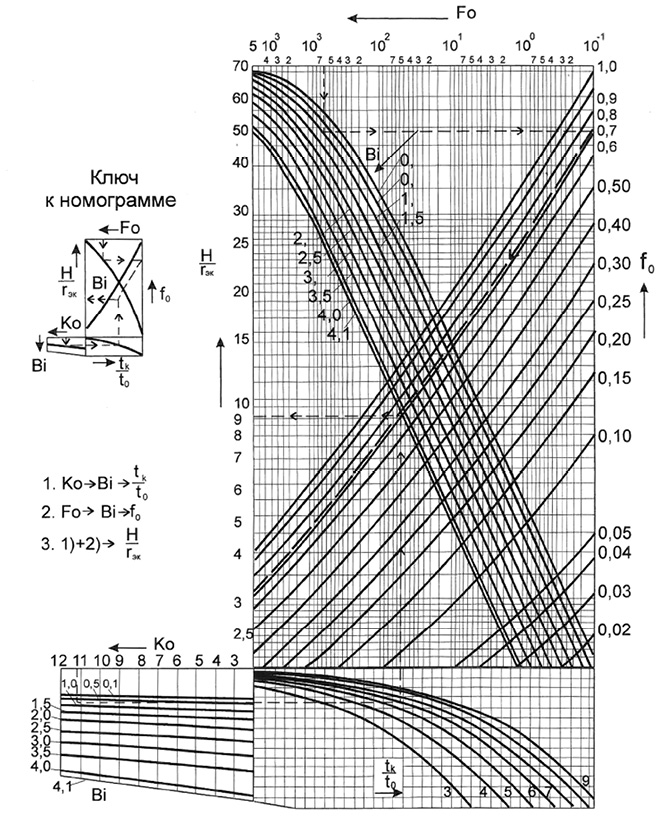
Рис. 4. Номограмма для определения талой зоны вокруг канала теплотрассы в сезоннопромерзающем грунте
Потом ведем ход решения с другой стороны номограммы. На шкале Fо находим точку с отметкой 608, из которой проводим вертикаль до пересечения с кривой Bi = 0,9. Из этой точки проводим горизонталь до пересечения со шкалой f0, откуда ведем ее параллельно кривой при значении f0 = 0,71 до пересечения с вертикалью от «немой» шкалы. Из точки пересечения ведем горизонталь до пересечения со шкалой H/rэк, где находим величину H/rэк = 9,1, после чего определяем H = 9,1•0,43 = 3,91 м. Величины талой зоны, определенные по формулам (7)–(9) и графоаналитическим методом по номограмме (рис. 4), совпадают. Приведенный графоаналитический метод максимально упрощает и облегчает расчет.
Выводы
1. C целью анализа температурного режима сезоннопромерзающего грунта были построены графики температурных полей вокруг канала теплопроводов по различным методикам и проведено их сравнение с экспериментальными данными, полученными в тождественных условиях. Установлено, что температурный режим грунта вокруг прямоугольных каналов теплопроводов в реальных условиях значительно отличается от полученного расчетным путем по формуле (4).
2. Для проверки соответствия того или иного теоретически рассчитанного температурного поля действительному распределению температур вокруг канала в грунте сравнивали идентичные поля (рис. 1 и 2). Сравнение показало, что кривые распределения температур в грунте, определенные по формуле (4) и приведенные на рис. 1, не соответствуют фактически замеренным на экспериментальных участках (рис. 2).
3. В результате суммирования собственного температурного поля от канала теплопроводов и естественного поля грунта было получено результирующее поле (рис. 3).
4. Трудоемкий процесс расчета температурных полей был значительно упрощен применением метода гидро- и электромоделирования.
5. Результаты экспериментальных данных были обработаны методом обобщенных переменных и получены зависимости (7)–(9).
6. В целях максимального упрощения и облегчения расчетов по формулам (7)–(9) составлена обобщенная расчетная номограмма (рис. 4), позволяющая легко рассчитывать величину талой зоны грунта вокруг канала теплотрассы.
7. Величины талой зоны, определенные по формулам (7)–(9) и графоаналитическим методом по номограмме (рис. 4), совпадают.
Исследования выполнялись на основании комплексной программы «Нефть и газ Западной Сибири».
Библиографическая ссылка
Моисеев Б.В., Земенков Ю.Д., Налобин Н.В. РАСЧЕТ ТАЛОЙ ЗОНЫ ГРУНТА ВОКРУГ КАНАЛА ТЕПЛОПРОВОДОВ // Успехи современного естествознания. – 2016. – № 8. – С. 188-194;URL: https://natural-sciences.ru/ru/article/view?id=36102 (дата обращения: 04.12.2024).