Для получения теоретической модели проводимости различных объектов (газовая плазма, растворы электролитов, твердое тело, в том числе и полимерные материалы), требуется привлечение наиболее общих принципов.
В решаемой задаче представляется естественным использование известного принципа электродинамики для эквивалентных представлений i через искомую проводимость l, напряженность внешнего электрического поля Е, числа Фарадея F, скорости движения зарядов V и плотности носителей тока n:
i = l•Е = n•е•V (1)
и четырехмерного уравнения движения в ковариантной форме:
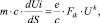(2)
где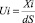 
– четырехмерная скорость; 
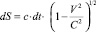– пространственный интервал при V << C, dS = cdt и Fik – антисимметричный ковариантный тензор электромагнитного поля. Скорость определяется четырьмя радиус векторами:
Xk = (ct, r); Xi = (ct, r). (3)
Из равенства (1) видно, что основной проблемой для нахождения l является установление скорости движения зарядов V, возможное строго лишь на основе уравнения (2), где тензор Fik для наглядности последующих рассуждений можно представить в виде
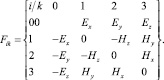(4)
Полагаем, что, электрическое поле Е направлено вдоль оси Еу и магнитное поле Н – вдоль оси z(Hz).
Уравнение (2) можно представить покомпонентно в развернутом виде и учитывать, что под дважды повторяющимся немым индексом подразумевается суммирование:
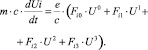(5)
Соотношение (5) допускает раздельный анализ для временной координаты I = 0 и пространственных K = 1, 2, 3. Для временной координаты имеет место при
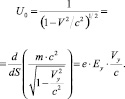(6)
Из матрицы видно, что при i = 0 магнитное поле Н отсутствует, скорость Vу направлена вдоль поля Еу. Движение ионов или зарядов подчиняется условию Vу << с, где с – скорость света. Возможно разложение V0, приведенное выше в ряд под степенями Vу/c, т.е. справедливо
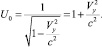(7)
Тогда для истинных траекторий движения зарядов с потенциалами
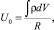
где r – плотность зарядов; dV = 4πr2dr – элемент объема; R – расстояние от точки наблюдения до dV, для левой части (7) имеет место аппроксимация:
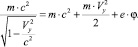, (8)
что формализует обобщенный импульс Рi [4].
Далее подставляя (8) в (7), при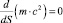 
и последующем интегрировании выражения
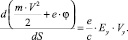
Приводим к равенству вида
.
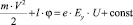По определению i•Ey•U = –eφ работа электрических сил, тогда const является внутренней энергией [5], поскольку слева – сумма кинетической и потенциальной энергий.
Отсюда, учитывая Максвелловское распределение по скоростям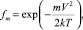 
получаем требуемое выражение для скорости движения зарядов:
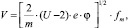(9)
где m – масса носителя тока; U – полная внутренняя энергия; fm – Максвелловское распределение по скоростям. Детальное описание этих величин приведено в работах [1, 2].
Следующий вариант анализа (5) связан с пространственными координатами I = 1, 2, 3 при заданной координате сил. Поскольку выбраны направления электрических и магнитных полей Ey и Hz при I = 2, то из уравнения (5) и матрицы (4) следует
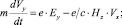(10)
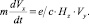(11)
Здесь учитывается, что U1 = U2 = -Vy/cn; Ui = U1 = Vx/c как ковариантные компоненты U – скорости.
Для решения уравнений (10) и (11) умножаем (9), мнимую единицу I складываем с уравнением (10). Это стандартная процедура в теории поля [1], при этом получаем уравнение
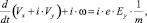(12)
где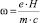 
– частота циклотронных колебаний.
Последующий анализ этого уравнения дан в [3]. Но если иметь в виду, что «компоненты скорости являются периодическими функциями от времени», то в (12) возможна стандартная аппроксимация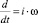 
. В этом случае, после очевидных преобразований, имеет место уравнение
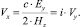(13)
Подставляя это значение Vx в (9), можно получить следующее равенство:
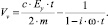(14)
Таким образом, найденные значения скоростей (13) и (14) для временной и пространственной компонент уравнения (4), при их последовательном использовании в (2), приводят к равенствам
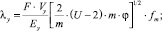(15)
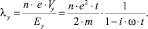(16)
Очевидно, что при Н = 0 имеет место w = 0 и выражение (16) трансформируется в формулу Друде для проводимости твердых тел:
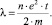(17)
Эта формула справедлива при классическом подходе и из квантовой механики. Поэтому её можно использовать для любых твердых тел, в т.ч. полимерных, полибензимидазолов (ПБИ).
В формуле Друде величина t является временем релаксации, т.е. временем свободного пробега носителя тока. Оно определяется выражением
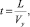(18)
где расстояние L соответствует расстоянию между атомами азота в элементарном звене макромолекулы ПБИ, равному ~9,11•10-18 см (квантовомеханический метод расчёта ММ+ с оптимизацией геометрии). Скорость движения Vy является тепловой:
При этих значениях L и Vy время релаксации равно
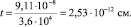
Диссоциация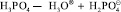 
дает концентрацию ионов:
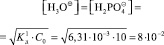
(при С0 = 10 моль/л = 4,8•1019 см-3).
Эти ионы ориентируются на свободные вакансии δ⊕ и δΘ на атомах азота в молекуле ПБИ. Их концентрации оцениваются из плотности:
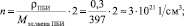
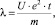
где U – плотность носителей тока или их число в 1 см3 объема ПБИ; t – время релаксации и m – протона, равная 1,66•10-24 г.
Формула Друде для решаемой задачи предполагает раздельный анализ n, t:
1. Для оценки n, предварительно можно оценить число свободных вакансий (атомы N), δ⊕ и δΘ , в 1 г ПБИ. По экспериментальной плотности ρ ≈ 1 г/см3
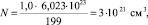
где 199 – эквивалентная масса элементарного звена полимера.
Эти вакансии занимают ионы образующиеся при диссоциации Н3РО4 на первой стадии:
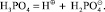
Молекулярные концентрации [Н⊕] и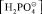 
оцениваются по Закону Оствальда по известной константе диссоциации для первой ступени 
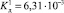. В частном случае выбираем концентрацию кислоты С0 = 11 моль/л. Тогда
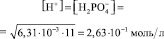
или число ионов в 1 см3 будет равно
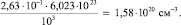
Видно, что эти величины достаточно близки N = 3•1021 см-1.
Для достаточного объема допирующего раствора Н3РО4 все вакансии будут заняты ионами Н⊕ и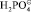 
, проводимость ПБИ – минимальна.
При числе ионов Н⊕ и 
больше чем N = 3•10-21 см3, возможен процесс: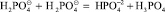 
причем один ион 
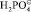, в положении δ⊕, а второй 
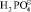образуется при диссоциации избытка Н3РО4 образующий протон Н⊕ является по существу свободным и может рассматриваться как носитель тока. Концентрация этих ионов оценивается по закону Оствальда для второй ступени диссоциации Н3РО4, при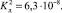 
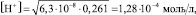
где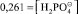 
. Если эту величину трансформировать в число ионов в 1 см3, то получаем значение n в формуле Друде:
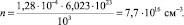
2. Значение времени релаксации t в формуле Друде находится по формуле
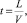
где L – расстояние между соседними δ⊕ или δΘ вдоль макромолекулярной цепи, и
Расчеты методом ММ+ показывают, что L = 9,11•10–8 см, тогда
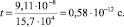
Подставляя найденные значения в формулу Друде, можно получить проводимость ПБИ в электростатической системе единиц, для которой l:
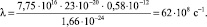
Для перевода этой величины См/см надо разделить её на размерный коэффициент 9•1011:
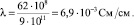
Экспериментальное определение протонной проводимости ПБИ, допированного 11 моль/л Н3РО4, составляет
λ = 6,7•10-3 См/см [6].
Таким образом, теоретически рассчитанное значение протонной проводимости ПБИ хорошо коррелирует с экспериментально полученными значениями.
Работа выполнена при финансовой поддержке Бурятского государственного университета № гранта 2016-16Е.
Библиографическая ссылка
Танганов Б.Б., Могнонов Д.М., Стельмах С.А., Балданова Д.М., Очиров О.С., Тоневицкий Ю.В. ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ ОЦЕНКИ ПРОТОННОЙ ПРОВОДИМОСТИ ПОЛИБЕНЗИМИДАЗОЛОВ, ДОПИРОВАННЫХ ОРТОФОСФОРНОЙ КИСЛОТОЙ // Успехи современного естествознания. – 2016. – № 9. – С. 34-37;URL: https://natural-sciences.ru/ru/article/view?id=36116 (дата обращения: 23.11.2024).