При исследовании изменений климата, с использованием данных многолетних наблюдений, возникает необходимость разложения временных рядов метеопараметров на основные составляющие. Если ряд не содержит сезонные компоненты, то задача сводится к разложению его на тренд, циклический тренд и случайную составляющие. К таким рядам относятся, например, многолетние ряды среднегодовых значений метеорологических параметров: среднегодовая температура, среднегодовое количество выпавших осадков и т.д. Анализу временных рядов посвящено много работ [1, 3, 4], в которых изложены основные методы обработки рядов, а программной реализации посвящена [2].
В данной работе проводится анализ и исследование временного ряда многолетних значений среднегодовой температуры в республике Крым (г. Симферополь). Сначала проведен предварительный статистический анализ исследуемых временных рядов. В табл. 1 приведены результаты такого анализа.
Таблица 1
Описательные статистики среднегодовой температуры Крыма
|
Пермен |
Средн |
Мин |
Макс |
Дисп |
Стд. отк |
Ст. ош |
Асим |
Эксц |
|
Ср темп Симфер |
10,826 |
8,747 |
12,753 |
0,7007 |
0,837 |
0,107 |
– 0,506 |
0,105 |
Из данных табл. 1 следует, что асимметрия отрицательная и умеренная, эксцесс положительный – слабый, а размах температуры достигает около четырех градусов. Эти результаты осредненные и не позволяют оценить динамику температуры.
Проведена проверка значимости тенденции роста среднегодовой температуры в современный период по сравнению с климатической нормой по критерию Крамера-Уэлча. Использование этого критерия, а не критерия Стьюдента, связано с тем, что для последнего не выполнены условия применимости. По критерию Крамера-Уэлча (sig. = 2,762 > 1,96) тенденция роста температуры значима на уровне р = 0,05.
Проведенный предварительный анализ свидетельствует о необходимости более глубокого анализа изменения среднегодовой температуры исследуемого региона.
Следуя методике [5], в работе проведено исследование, построена модель и вычислены прогнозные значения временного ряда среднегодовой температуры.
Результаты предварительного анализа показывают, что для описания временного ряда значений среднегодовой температуры его можно представить аддитивной моделью вида
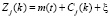 , k = 1,2,…N, (1)
, k = 1,2,…N, (1)
где N – число членов ряда, j = 1,2 – номер пункта наблюдения, Сj(k) – циклический тренд, подлежащий определению, а ξ – случайная часть с нормальным законом распределения, с нулевым математическим ожиданием, k – номер ряда, m(t) – линейный тренд, определяемый по формуле
m(t) = n + kt,
где коэффициенты n, k определяются методом наименьших квадратов.
После выделения полиномиального тренда ряд содержит только циклический тренд и нерегулярную часть.
Для выделения циклических составляющих временного ряда и программной реализации широко используется спектральный анализ рядов [2–4]. Однако, как известно, для использования результатов спектрального анализа для построения моделей прогнозирования, необходимо их дополнить различными критериями выбора основных периодов. Следуя [5], в данной работе в качестве дополнительных критериев используются критерии случайностей остатка ряда, а также критерии, основанные на согласовании полученных результатов с результатами широко известных методов сглаживания временных рядов.
В качестве критериев случайностей остатка ряда используются число поворотных точек, статистика Дарбина-Уотсона автокорреляционные функции и коэффициенты корреляции Пирсона. Критериями проверки циклического тренда выбраны метод классической декомпозиции и метод, основанный на использовании фильтра 4253Н.
Разлагая центрированный временной ряд значений метеопараметра в ряд Фурье, построены периодограмма и спектр ряда по известным формулам.
Периодограмма ряда определяется по формуле
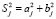 ,
, 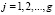 , (2)
, (2)
где aj и bj коэффициенты разложения Фурье ряда, определяемые по известным формулам:
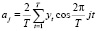 , (3)
, (3)
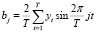 ,
, 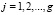 (4)
(4)
При четном Т, к ним добавляется
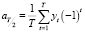 .
.
В результате анализа получен линейный тренд ряда, определяемый по формуле
m(t) = 10,35 + 0,015*t,
где t – время.
Отсюда следует, что наблюдается повышение среднегодовой температуры, что объясняется, по-видимому, антропогенными факторами и согласуется с теорией глобального потепления климата. Для выделения остальных составляющих временного ряда необходимо исключить линейный тренд из ряда. Тогда получим центрированный временной ряд, который можно рассматривать как стационарный и к нему можно применить спектральный анализ.
Так как периодограмма ряда является случайной, проводится ее сглаживание, используя спектральные окна, в частности, использовано окно Хемминга с шириной окна m = 5. Формула Хемминга определяется в виде
wj = 0,54 + 0,46*cos(π*j/p) (для j = 0 до p), w-j = wj (для j ≠ 0).
Результаты такого анализа для временного ряда центрированных значений среднегодовой температуры, периодограммы гармоник и спектральная плотность приведены на рис. 1.
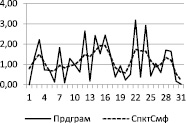
Рис. 1. Периодограмма и спектр среднегодовой температуры Крыма
Из графиков видно, что периодограмма имеет относительно большое число пиков, а спектр ряда – пять наиболее ярко выраженных максимумов, в области которых проводится поиск значимых гармоник.
Как известно, для оценки степени корреляции используется статистика Дарбина-Уотсона, определяемая по формуле
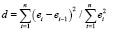 , (5)
, (5)
где ej – остаток ряда.
Составлены соответствующие программы на языке высокого уровня и проведены расчеты. По статистике (5) проведен анализ остатка ряда, последовательно включая в циклический тренд пробные гармоники, полученные по результатам спектрального анализа.
Одним из критериев адекватности модели является невязка, определяемая по формуле
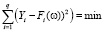 , (6)
, (6)
где Yi, Fi – фактические и модельные значения ряда, соответственно.
Аналогичные исследования проведены и по другим критериям.
В табл. 2 приведены значения критериев для различных вариантов, по которым осуществляется выбор основных периодов.
Таблица 2
Значения критериев случайностей остатка ряда температуры
|
Периоды (лет) |
Критерий Дарбина-Уотсона |
Число поворотных точек |
Невязка ( °С) |
Коэффициенты корр. Пирсона |
||||
|
Фкт- прогноз |
Дек- прогноз |
4253Н-пргоноз |
||||||
|
факт. |
теор. |
факт. |
теор. |
|||||
|
60, 10, 4,6, 2,9 |
2,19 |
2 |
36 |
38,7 |
23,3 |
0,55 |
0,46 |
0,40 |
|
60, 10, 4,6 |
2,12 |
– |
34 |
– |
33,9 |
0,31 |
0,49 |
0,52 |
|
60, 10, 2,9 |
2,11 |
– |
35 |
– |
26,7 |
0,50 |
0,49 |
0,49 |
|
60, 10 |
2,17 |
– |
36 |
– |
31,6 |
0,37 |
0,68 |
0,73 |
|
10, 4,6, 2,9 |
2,21 |
– |
36 |
– |
44,7 |
0,16 |
0,37 |
0,38 |
Из данных таблицы следует, что по комплексу параметров наиболее подходит вариант 3 (3 строка), так как большинство критериев соответствует теоретическим значениям, немного уступая по некоторым критериям 4-му варианту (4 строка). Однако вариант 3 лучше по значениям АКФ (см. рис. 2), кроме того, в 4-м варианте отсутствует частота, соответствующая максимальному значению спектра. Поэтому выбирается 3-й вариант с периодами: 60, 10, 2,9 лет.
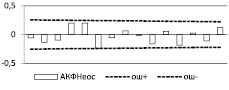
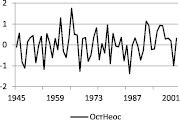
Рис. 2. АКФ остатков ряда (слева) и остатков ряда (справа)
На рис. 2 приведены некоторые результаты такого анализа.
Видно, что АКФ остатка ряда, полученного как разность фактических и модельных значений выбранного варианта, удовлетворяет условию случайности на уровне р = 0,05. По графику остатков ряда (справа) определяется число поворотных точек, теоретическое значение определяется по формуле [3]:
N = 2/3(n – 2). (4)
Далее проведены аналогичные исследования для оценки регулярной части ряда, а именно по согласованию результатов модели, с результатами широко используемых методов сглаживания рядов, в частности, метода классической декомпозиции и фильтра 4253Н. Ниже, на рис. 3 приведены результаты такого анализа.
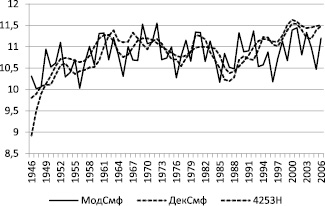
Рис. 3. Графики значений среднегодовой температуры: по модели (сплошная), метод классической декомпозиции (точечная) и фильтра 4253Н (пунктирная)
Из графиков рисунка видно, что методы классической декомпозиции и фильтра 4253Н дают более сглаженные значения по сравнению с результатами модели, которые более точно отражают основные характеристики исходного ряда, но в целом они согласуются между собой.
Окончательный выбор параметров модели проводится по наилучшему согласованию (по минимуму невязки) с учетом всех критериев.
В результате для среднегодовой температуры Крыма получена модель вида:
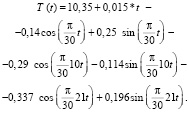 (6)
(6)
По формуле (6) проведены расчеты прогнозных значений до 2035 года. На рис. 4 приведены графики фактических и прогнозных значений ряда.
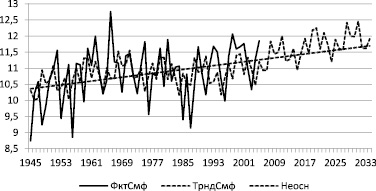
Рис 4. Фактические (сплошная линия) и прогнозные (пунктирная линия) значения среднегодовой температуры Крыма
Из рис. 4 видно, что прогнозные значения ряда изменяются достаточно сложно в соответствии с моделью (6). На фоне повышения в среднем среднегодовой температуры, от 10,5 до 11,7 градусов, наблюдаются циклические колебания. Наибольшие значения среднегодовая температура будет принимать в 2007–2015, 2021–2025 и 2029–2033 годы, а наименьшие – в 2017–2019 и 2026–2028 годах. Для оценки точности метода, на рисунке (справа), приведены графики фактических и прогнозных значений ряда за последние 10 лет.
Относительная ошибка прогноза определяется по формуле

где yфi, yпi – фактические и прогнозные значения ряда, соответственно
Для оценки точности прогноза проведено прогнозирование последних членов ряда, результаты которых приведены в табл. 3.
Таблица 3
Фактические и прогнозные значения ряда
|
Факт. |
9,98 |
11,4 |
12,1 |
11,6 |
11,7 |
11,8 |
11 |
10,3 |
11,3 |
11,8 |
Ср |
|
Прогн. |
10,2 |
10,7 |
11,1 |
10,7 |
11,4 |
11,4 |
10,8 |
11,3 |
11,0 |
10,5 |
|
|
Отн. ош. |
1,96 |
5,83 |
7,75 |
7,94 |
2,37 |
2,73 |
1,72 |
9,6 |
2,76 |
11,6 |
5,4 |
Как видно из табл. 3, средняя относительная ошибка последних 10 членов равна 5,4 %, максимальная среди них равна 11,6 %, которые свидетельствуют о высокой точности прогноза.
Библиографическая ссылка
Хаупшева М.Х., Шугунов Т.Л., Шугунов Л.Ж. АНАЛИЗ И ПРОГНОЗ ЗНАЧЕНИЙ СРЕДНЕГОДОВОЙ ТЕМПЕРАТУРЫ КРЫМА С ИСПОЛЬЗОВАНИЕМ КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ // Успехи современного естествознания. 2017. № 1. С. 100-104;URL: https://natural-sciences.ru/ru/article/view?id=36349 (дата обращения: 14.02.2026).



