Основной технологией используемой для увеличения нефтеотдачи является применение системы поддержания пластового давления (ППД). Одной из основных функций системы ППД является вытеснение нефти к забоям добывающих скважин. Расчет технологических показателей разработки, учитывающей особенности вытеснения нефти водой и изменения характера фильтрационных процессов в пласте, разработан Ю.П. Борисовым (методики ВНИИ-1, ВНИИ-2) [2]. В данной работе рассматриваются нестационарные фильтрационные потоки, зависящие от выбранных краевых условий, которые авторы назвали трансформацией фильтрации.
На первой стадии разработки, пока система ППД не сформирована, падение давления в зонах работы добывающих скважин в плоскости XY подчиняется законам плоскорадиальной фильтрации. На второй стадии разработки характер распределения пластового давления в залежи начинает изменяться, в зависимости от сроков ввода в эксплуатацию нагнетательных скважин и их размещения по отношения к добывающим скважинам.
С течением времени при одновременной эксплуатации скважин радиус фронта вытеснения Rnag увеличивается и превысит расстояния между скважинами. Аналогичная картина должна происходить и с радиусом контура питания добывающей скважины. Поскольку давления в окрестности нагнетательной скважины превышают начальное пластовое и забойные давления добывающих скважин Pnag > P0 > Pc, то большая часть потока закачиваемой воды устремляется к добывающим скважинам. Плоскорадиальная фильтрация изменяется, трансформируется, и в пласте возникают области, зоны прямолинейной-параллельной (линейной) фильтрации.
Таким образом, процесс фильтрации флюидов происходит в три стадии:
1-я стадия. Плоскорадиальная фильтрация имеет место до того момента времени, при котором сумма радиусов вытеснения и питания равна расстоянию между скважинами.
2-я стадия. Начинает формироваться линейная фильтрация по линии между добывающей и нагнетательной скважинами – области А и В;
3-я стадия. На третьей стадии возникают перетоки флюидов между линейными областями А и В и окружающими зонами 1 и 2, вообще говоря, неравных, с давлениями в зонах 1 и 2 – Р1 и Р2 соответственно. Причем перетоки со скоростями V1, V2 происходят не сразу, запаздывают. Из области пласта А происходит переток закачиваемой воды в зону 1 окружающую область, а из зоны 2 приток пластовой воды и нефти в область линейной фильтрации В. Таким образом, некоторый объем закачиваемой в пласт воды не участвует в вытеснении нефти. Вода, поступившая в зону 1, увеличивает обводненность и уменьшает подвижность содержащейся в ней нефти. Следовательно, в пласте существует сечение GG1с давлением равным начальному пластовому P0.
Эпюры скоростей фильтрации и распределения давления в линейной области приведены на рис. 3.
Отметим, что наличие в пласте существования сечения GG1 с давлением равным начальному, пластовому отмечено Ю.П. Желтовым в [5]. Формирование областей и зон линейной фильтрации подтверждается многочисленными трассерными исследованиями, проведенными на месторождениях Западной Сибири [10].
Время трансформации зависит от ФЕС пласта, свойств флюидов и технологических показателей. Для однородного пласта широко используется формула
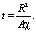(1)
Для слоистого пласта, состоящего из m пропластков (прослоев разной проницаемости) с одинаковыми или близкими коэффициентами упругоемкостями, для однородного флюида из (1) получим соотношение
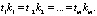(2)
В формулах (1), (2):
1) не учитываются перетоки между пластом и областью линейной фильтрации;
2) отсутствует зависимость от технологических показателей разработки.
Процессы фильтрации и вытеснения нефти водой зависят от заданных краевых условий. В данной статье рассматриваются граничные условия с известными постоянными дебитом и приемистостью.
Рассмотрим отдельно каждую стадию.
1-я стадия. Переход от плоскорадиальной фильтрации к линейной.
Рассмотрим элемент эксплуатационного объекта, состоящего из двух скважин: добывающей и нагнетательной. Для простоты пласт будем считать однородным, изотропным.
Начало координат совместим с забоем добывающей скважины. Рассмотрим два случая:
1) аномальные коллекторы, к которым относятся залежи, насыщенные высоковязкой нефтью ипласты с низкими фильтрационными свойствами. Фильтрация описывается обобщенным законом Дарси с начальным градиентом давления;
2) коллекторы, в которых выполняется классический закон Дарси.
1. Аномальные коллекторы.
Уравнение пьезопроводности для аномальных коллекторов имеет вид
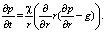(3)
Краевые условия:
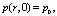
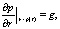
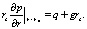(4)
Согласно методу интегральных соотношений [1] решение (3) ищем в виде
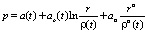, (5)
коэффициенты a определяются из краевых условий (4). Параметр α ≥ 1 и подбирается из соответствия фактических и расчетных значений.
Обозначим
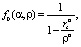
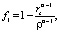
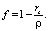
Тогда коэффициенты ai равны
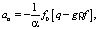
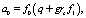
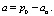(6)
Для определения зависимости ρ(t) проинтегрируем (3) по r в пределах от rc до ρ(t). В результате получим кубическое уравнение относительно ρ(t)
.
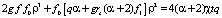Приближенное решение, которого имеет вид
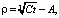
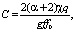
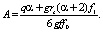(7)
Из (7) следует, что для аномальных коллекторов, фильтрация, в которых не подчиняется классическому Дарси, радиус текущего контура питания пропорционален корню кубическому от времени. Зависит от физических свойств нефти, коллектора и дебита скважины – технологического показателя.
Для нагнетательной скважины уравнение пьезопроводности имеет вид
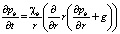. (8)
Если начало координат совместить с забоем нагнетательной скважины, то краевые условия примут вид
, 
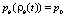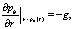
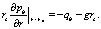(9)
Индекс b относится к воде. Градиент давления в зоне нагнетания отрицателен, поэтому в правой части (8) взят знак «+». Решение (8) ищем в виде (5). После преобразований получим кубическое уравнение и приближенную формулу аналогичную (7) для определения радиуса контура вытеснения
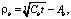
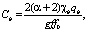
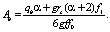(10)
Время начала формирования линейной фильтрации t0* между нагнетательной и добывающей скважинами определяется из условия
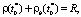(11)
где R – расстояние между скважинами. Подставляя (7) и (10) в (11), получим
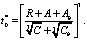(12)
Для оценки полученного выражения, учитывая, что A и Ab много меньше R, рассмотрим приближенное значение (12)
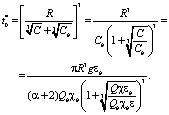(13)
Откуда следует, что с ростом начального градиента g время начала трансформации увеличивается. Это обусловлено низкими скоростями фильтрации в аномальных коллекторах.
Пример 1. Рассмотрим высокопроницаемый коллектор, насыщенный вязкопластичной нефтью (ВПН). Расчеты показали, что при rc = 0,1 м, для α в интервале от 1,0001 до 3 и ρ в интервале от 1 м до 200 м, функции f(α) и f0(α) практически равны 1. Дано:
R = 400 м, h = 10 м, μn = 300 мПас, μb = 1 мПас, βb = 2*10-4/МПа-1, g = 0,1 МПа/м, βn = 12*10-4/МПа-1, βс = 1*10-4/МПа-1, m0 = 0,2, kb = 1*10-13м2, kn = 2*10-13м2, Q = 10м3/сут, Qb = 40 м3/сут, rc = 0,1 м, f1 = 0,8.
С увеличением параметра α время уменьшается, но радиусы практически не изменяются. С увеличением приемистости Qb время и ρ уменьшаются, ρb возрастает и смещается в сторону добывающей скважины. Так при Qb = 40 м3/сут и α = 1,01 значения р = 125 м, αb = 275 м, t0* = 77 сут. С ростом приемистости размеры областей и время изменяются, другой вопрос – будет ли пласт, насыщенный ВПН, принимать такое количество воды без нарушения структуры и разрушения призабойной зоны пласта нагнетательной скважины. Коллекторы, содержащие ВПН, как правило, слабосцементированы, наблюдается значительный вынос механических примесей. Большое значение имеет величина начального градиента давления, которая, по данным обработки результатов гидродинамических исследований скважин Русского месторождения, изменяется в пределах от 0,02 до 0,437 МПа/м [7].
Таким образом, время начала трансформации плоскорадиальной фильтрации для аномальных месторождений зависит от технологических параметров, физических свойств коллектора и флюидов.
2. Коллекторы, в которых выполняется закон Дарси.
Для плоскорадиальной фильтрации, подчиняющейся классическому закону Дарси, в уравнениях пьезопроводности (3) и (8) и в краевых условиях (4) и (9) следует положить g = 0. Соответственно изменятся коэффициенты (6), и в результате для определения радиусов контура питания и фронта вытеснения получим квадратные уравнения, откуда
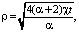
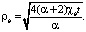(14)
В отличие от (13) зависимость времени трансформации от расстояния между скважинами квадратичная, от технологических показателей разработки не зависит. Радиусы зависят только от физических свойств коллектора и флюидов.
Время начала формирования линейной фильтрации t00* равно
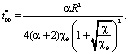(15)
При подстановке (15) в (14) получим, что радиусы равны р = 133м, рb = 267 м и от параметра α не зависят. Сечение GG1 расположено на расстоянии 133 м от забоя добывающей скважины.
Если для определения времени начала трансформации использовать формулу (1) и условие (11), то время начало трансформации t0 равно
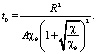(16)
Ниже приведен расчет времени начала трансформации плоскорадиальной фильтрации.
Пример 2. R = 400 м, h = 10 м, μn = 3 мПас, μb = 1 мПас, βb = 2*10-4/МПа-1, βn = 12*10-4/МПа-1, βс = 1*10-4/МПа-1, m0 = 0,2, kb = 1*10-13 м2, kn = 2*10-13 м2.
С ростом числового параметра α время начала трансформации t00* возрастает. С увеличением А время t0 убывает, при А = 12 и α = 1 – 1,01 t00* = t0.
Заметим, что А = 12 соответствует радиусу контура питания, подсчитанному методом Баренблатта. Для заданных параметров значения радиусов контура питания и вытеснения равны ρ = 133м, ρb = 267м. От параметров α и А не зависят. Результаты расчетов соответствуют одновременному введению в эксплуатацию добывающей и нагнетательной скважины. Если нагнетательная скважина введена в работу позже начала эксплуатации добывающей скважины, что обычно и бывает, то следует изменить первое краевое условие (9) для расчета давления в окрестности нагнетательной скважины.
2-я стадия. Линейная фильтрация в областях А и В.
Рассмотрим формирование линейной области фильтрации между добывающей и нагнетательной скважинами. Переток флюидов между областями и зонами отсутствует. В дальнейшем будем рассматривать фильтрацию соответствующую классическому закону Дарси.
Уравнение пьезопроводности для добывающей скважины имеет вид
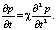(17)
Выбор краевых условий, как отмечалось в других работах авторов данной статьи, существенно влияет на процессы фильтрации, расчетные технологические показатели разработки и в конечном счете на нефтедобычу. Поэтому рассмотрим два случая задания краевых условий.
2.1. Зададим краевые условия в виде
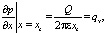
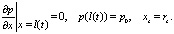(18)
Для решения (17) с краевыми условиями (18) воспользуемся методом интегральных соотношений, в результате получим
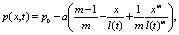
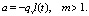(19)
Линейный размер области возмущения В равен
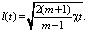(20)
Распределение давления в области А и линейный размер lb(t), характеризующий работу нагнетательной скважины, определим аналогично с заменой дебита на приемистость
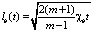. (21)
Время окончания 2.1 стадии t2*определим из условия (11)
Откуда
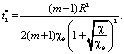(22)
Если формально положить m = α + 1, то получим, что t2* = 2t00*. Таким образом, время установления линейной фильтрации в два раза больше времени начала трансформации – перехода плоскорадиальной фильтрации в линейную фильтрацию для коллекторов, насыщенных маловязкими нефтями. Соответственно, формулы (20) и (21) примут вид
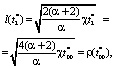
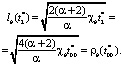(23)
Следовательно, в этом случае, сечение GG1 не изменяет своего положения в пространстве. Время установления линейной фильтрации t2*, l(t2*) и lb(t2*) для разных α можно определить.
Вообще говоря, параметры α и m не равны, поскольку характеризуют различные процессы фильтрации: плоскорадиальную и прямолинейно-параллельную. Подбор параметров следует осуществлять посредством сравнения промысловых и расчетных данных. Следует отметить, что третье краевое условие (18)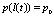 
соответствует невозмущенному состоянию в залежи. Далее рассмотрим краевые условия, учитывающие связь давлений на первой и второй стадиях.
2.2. В отличие от пункта 2.1 запишем третье краевое условие (18) в соответствиипластовому давлению на момент окончания плоскорадиальной фильтрации:
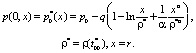(24)
Применяя метод интегральных соотношений, получим
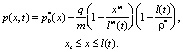(25)
Дифференциальное уравнение для определения l(t) примет вид
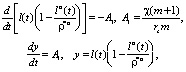(26)
После интегрирования получим трансцендентное уравнение относительно l(t)
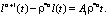
Положим m = α и рассмотрим, какие значения может принимать l(t).
Для x = l(t) давление равно
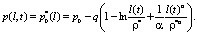
Из (25) следует, что при l(t) = ρ* p(l(t)) = p0, а при l(t) > ρ*, p(l) > p0, что не имеет физического смысла, следовательно, l(t) ≤ ρ*. Таким образом, при трансформации плоскорадиальной фильтрации в линейную фильтрацию граница GG1 не перемещается. Тот же самый результат получим, если рассмотреть эксплуатацию нагнетательной скважины. Следовательно, задание начального условия (24) является определяющим для величин давления в областях линейной фильтрации и определения положения границы начального пластового давления GG1.
Время установления линейной фильтрации t2* для различных α равно t00* поскольку отсчет времени t2*начинается от 0. В отличие от пункта 2.1 граничное условие (24) осуществляет связь между окончанием плоскорадиальной фильтрации и началом линейной фильтрации. Хотя выбор третьего граничного условия не изменяет положения сечения GG1, но является более строгим и точнее отражает физические процессы, имеющие место при эксплуатации скважин. Отметим, что значения времен значительно меньше времени эксплуатации скважин.
3-я стадия. Линейная фильтрация в областях Аи В с перетоками между областями и зонами.
Процесс перетоков флюидов между областями и зонами начинается с запаздыванием, зависит от распределения давлений на границах между областями и зонами ФЕС коллектора.
Рассмотрим прямолинейно параллельную (линейную) фильтрацию в областях А и В с учетом перетока воды из А в зону 1 и притока жидкости из зоны 2 в область В.
Уравнение пьезопроводности в области В имеет вид [3, 6]
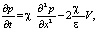(27)
где V – скорость перетока из зоны 2 в область В. Точное значение скорости перетока приведено в [6], приближенное – имеет вид:
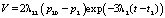, (28)
где λ2, λ22 параметры, характеризующие фильтрационные свойства зоны 2, t2 – время достижения границы зоны 2, при t < t2 экспонента равна 1, p20 – давление на границе зоны 2 и области В. Отметим, что наибольшие значения скорость перетока принимает при t < t2. При t>→∞ скорость перетока стремится к нулю, массобмен между зонами и областями прекращается. Давление в области соответствует стационарной фильтрации.
Давление p20 на границе области В и зоны 2 получим из выражения (25) при l(t*2) = р*, которое соответствует условию (24).
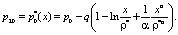
Применяя метод интегральных соотношений, получим выражение для определения давления
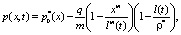
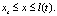(29)
Выражение (29) аналогично ранее полученному выражению (25). По аналогии с пунктом 2.2 имеем, что граница (сечение) GG1 не смещается.
Таким образом, на рассмотренном примере элементарного участка эксплуатационного объекта, состоящего из нагнетательной и добывающей скважины, изменяются фильтрационные потоки. Плоскорадиальная фильтрация трансформируется в линейную, что существенно влияет как на распределение давления, так и на нефтеотдачу. Граница GG1 при заданных краевых условиях, соответствующих постоянному дебиту и постоянной приемистости, не изменяет своего положения в пространстве. Согласно вышеизложенному при выбранном α время формирования плоскорадиальной фильтрации t00*, время формирования линейной фильтрации t2* и время запаздывания (формирования) перетоков равны между собой tп. Общее время трансформации будет равно t* = 3t00*, и для различных значений параметра α будет изменяться в пределах от 7 до 12,5 ч, что, конечно, мало по сравнению со временем эксплуатации скважин, но возникновение и продолжительность перетоков между областями и зонами изменяет в них коэффициенты насыщенности. А значит, безусловно, скажется на прогнозировании результатов применения методов увеличения нефтеотдачи (МУН). Проблемы извлечения остаточной нефти подробно рассмотрены в [8]. Применение физико-химических и гидродинамических МУН тесно связано с фильтрационными процессами, поэтому трансформация потоков флюидов будет влиять на текущую нефтеотдачу. Действительно, использование закачки водных растворов химических реагентов приведет к тому, что часть из них перетекает в зону 1 и непосредственно в увеличении добычи нефти не участвует. На наш взгляд, наиболее успешно совместное применение физико-химических методов с циклическим заводнением и изменением фильтрационных потоков. Для этого необходимо знать количества (объемы) жидкостей, перетекающих между областями и зонами.
Основным условием, характеризующим количество закачиваемого, добываемого и перетекающих флюидов, является закон сохранения масс, учитывающий изменение остаточной нефти и воды в областях, охваченных разработкой. Количество остаточных флюидов зависит от физических свойств коллектора, гидрофильности и гидрофобности отдельных участков пласта, от изменения коэффициентов насыщенности и коэффициентов фазовых проницаемостей.
Если завимостями плотностей от давления и температуры пренебречь, то в первом приближении уравнение баланса масс для закачиваемой воды примет вид
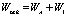. (30)
Для добывающей скважины объем добытой жидкости Wdob зависит от объемов жидкостей WB в области В и объема W2, притекающего из зоны 2.
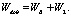(31)
Коэффициент компенсации определяется соотношением
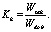(32)
С течением времени скорости перетоков падают, текущие (но не накопленные) объемы W1, W2 стремятся к нулю, следовательно, текущий коэффициент компенсации будет равен
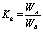. (33)
То есть будет определяться объемами флюидов в областях А и В, по которым осуществляется линейная фильтрация. Для коллекторов, в которых выполняется классический закон Дарси, из (7.42) для постоянных площадей фильтрации, коэффициента пористости и формул (7.14) получается следующее соотношение
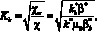
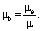(34)
Из (34) по известному из промысловых данных коэффициенту компенсации можно определить фильтрационные параметры пласта. Если пренебречь изменением коэффициентов вязкости и упругоемкости от давления, то из (34) можно определить изменение отношения относительных фазовых проницаемостей. Заметим, что накопленные объемы флюидов в зонах стремятся к постоянным величинам, которые определяются ФЕС пласта и выбранной системой разработки.
В работе авторов [4] рассмотрены фильтрационные процессы в гидрофильных и гидрофобных коллекторах, учитывающие капиллярное давление и начальный градиент. Доля движущейся воды в пласте описывается обобщенной функцией Бакли-Леверетта. Если начальным градиентом и изменением капиллярного давления пренебречь, то на забое добывающей скважины функция Бакли-Леверетта равна коэффициенту обводненности [5]
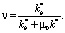(35)
Таким образом, контролируя два технологических показателя – определить изменение каждого коэффициента относительной фазовой проницаемости в процессе разработки.
Для аномальных коллекторов, в которых выполняется обобщенный закон Дарси, и доля движущейся воды в пласте описывается обобщенной функцией Бакли-Леверетта [4]. На забое добывающей скважины r = rc коэффициент обводненности равен
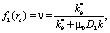
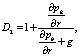(36)
где
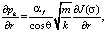
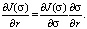
Из решения уравнения (8) получим, что производная текущего давления pb при r = rc равна
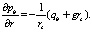
Параметр D2 примет вид
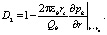(37)
На забое нагнетательной скважины при предельном водонасыщении σ* = 0,6 – 0,8 производная функции Леверетта ≈ 0, следовательно, D2 ≈ 1. После подстановки в (36) получим, что коэффициент обводненности соответствует соотношению (35), н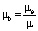о 
мало.
Для определения коэффициента компенсации в данном случае используем формулы (33), (7) и (10)
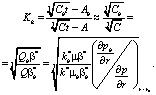(38)
Если градиенты давлений имеют один порядок, (а корень кубический), то приближенное значение коэффициента компенсации можно представить в виде
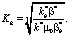(39)
Таким образом, для маловязких нефтей для определения коэффициентов относительных проницаемостей по технологическим показателям имеем два соотношения (34) и (35):
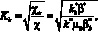
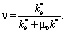
Для аномальных коллекторов следует использовать соотношения (35) и (39):
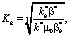
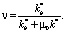
Для расчета скоростей перетока флюидов между областями и зонами можно воспользоваться методами, разработанными в монографии [9], в которой рассматривается приток (расход) жидкости к вертикальной трещине. В качестве вертикальной трещины следует рассматривать области А и В. Заметим, что в [9] учитывается несовершенство вскрытия и анизотропия коллектора.
Выводы
1. При разработке нефтяных месторождений в пласте между добывающей и нагнетательной скважинами существует сечение GG1, с давлением равным начальному пластовому. Плоскорадиальная фильтрация трансформируется в прямолинейно-параллельную. В окрестностях скважин возникают зоны перетока флюидов в окружающее пространство.
2. Получены формулы и приведены примеры по определению положения и времени образования сечения GG1 в зависимости от выбранных краевых условий для залежей смаловязкимии высоковязкими нефтями. Показано, как влияет выбор граничных условий на формирование фильтрационных потоков.
3. Разработана методика расчета относительных фазовых проницаемостей по известным технологическим показателям – коэффициентам обводненности и компенсации.
4. Если на забоях скважин задать постоянные давления отбора и нагнетания, то граница GG1 не совпадет с ранее рассмотренным случаем. В процессе эксплуатации скважин режимы работы изменяются, необходимо учитывать интерференцию, взаимовлияние, по крайней мере, близ расположенных скважин, ну, конечно, систему разработки – размещение скважин, которая также может меняться. По картам изобар, построенных для различных времен эксплуатации объекта, можно приближенно определить, как смещается граница GG1 при изменении режимов работы скважин.
5. При выводе полученных формул граничным условием являлись постоянный дебит добывающей скважины и приемистость нагнетательной скважины. Если известны законы их изменения во времени, то приведенные выше распределения давлений и формулы изменятся, но трансформация процесса фильтрации останется. Если на забоях добывающей и нагнетательных скважин задать забойные давления – вместо дебита и расхода, то и в этом случае нетрудно (но утомительно) записать соответствующие формулы и соотношения.
6. Предложенную методику трансформации фильтрационных потоков, используя принцип интерференции скважин, можно обобщить и применить для большего количества скважин с выбранной системой разработки. Отметим, что карты изобар и текущей нефтенасыщенности, построенные с учетом трансформации фильтрационных потоков, не будут совпадать с картами, построенными по общепринятой методике.
Надеемся, что все вышеизложенное послужит для дальнейшего совершенствования гидродинамических моделей разработки месторождений углеводородов.
Библиографическая ссылка
Коротенко В.А., Грачев С.И., Кушакова Н.П., Сабитов Р.Р. ТРАНСФОРМАЦИЯ ПРОЦЕССОВ ФИЛЬТРАЦИИ ПРИ РАЗРАБОТКЕ ЗАЛЕЖЕЙ УГЛЕВОДОРОДОВ // Успехи современного естествознания. – 2017. – № 2. – С. 86-93;URL: https://natural-sciences.ru/ru/article/view?id=36368 (дата обращения: 03.12.2024).