Данные глобальных навигационных спутниковых систем (ГНСС), в первую очередь американской системы GPS, уже более 25 лет успешно используются в геодинамических исследованиях, наблюдениях за вулканической активностью и в сейсмологии [14].
В результате так называемой кинематической обработки ГНСС-измерений можно формировать временные серии (ряды) координат геодезических пунктов с малым шагом дискретизации 1 с и менее [2, 4], т.е. практически мгновенных положений ГНСС-станций. С их помощью получают записи сейсмических волн, генерируемых сильными землетрясениями. Таким образом, ГНСС-оборудование может быть использовано в качестве сейсмометра [1].
Основные преимущества ГНСС-технологий перед классическими сейсмическими инструментами заключаются в возможности регистрации сколь угодно сильных колебаний земной поверхности любых периодов без искажения фазы и амплитуды [1], основной недостаток – высокий уровень шума, обусловленный сантиметровой точностью определения мгновенных координат [4, 8].
В координатных рядах, полученных обработкой ГНСС-измерений, можно выделить две составляющие. Одна из них – полезный сигнал – обусловлена перемещениями антенны вследствие, например, природных или техногенных подвижек земной поверхности или прохождения сейсмических волн. Другая составляющая – шум – совместное действие случайных, систематических и грубых ошибок на результаты определения координат.
Исследование характеристик шума временных рядов ГНСС-координат имеет большое практическое значение, так как может дать информацию о его причинах и позволяет судить о надежности и точности выделения «полезного сигнала» из исходного координатного ряда. Наиболее просто и удобно определять характеристики шума, используя ряды, которые полезного сигнала не содержат.
Обзор более 15 работ, посвященных моделированию шума в рядах координат, получаемых обработкой данных ГНСС-измерений, можно найти в [11]. Во всех этих работах обработка данных ГНСС-измерений выполнена методом относительного позиционирования, т.е. определялись взаимные перемещения пары спутниковых приемников, установленных в стабильной точке с известными координатами (база) и определяемой подвижной точке (ровер). Вектор, компонентами которого являются разности координат базы и ровера, называется базовой линией, а расстояние между базой и ровером, определяемое модулем этого вектора, называется длиной базовой линии.
В большинстве вышеупомянутых исследований использовались короткие базовые линии (до 10 км), в то время как на практике приходится обрабатывать векторы длинной в сотни километров. Относительное позиционирование обеспечивает высокую точность получения компонент базовой линии, однако любые изменения координат базовой станции приводят к соответствующим искажениям вычисляемых положений ровера. Подобная ситуация обычно возникает при получении волновых форм сейсмических колебаний, инициированных сильными землетрясениями. Поэтому возможности применения относительного метода в сейсмологии весьма ограничены.
В настоящей работе выполнено моделирование шума рядов координат, получаемых при обработке ГНСС-данных методом Precise Point Positioning (PPP) [15] в режиме реального времени. Этот метод позволяет получать мгновенные значения абсолютных координат без привязки к базовым станциям и является предпочтительным для получения волновых форм землетрясений и основным при обработке данных ГНСС-измерений в режиме реального времени [8]. Построенные модели шума рядов координат сопоставлены со стандартными моделями сейсмического шума [5, 13], что позволяет делать выводы о возможности применения ГНСС-аппаратуры для решения сейсмологических задач и/или совместного использования с сейсмическими инструментами.
Материалы и методы исследования
В качестве исходных данных были использованы наблюдения с шагом дискретизации 1 с, полученные на 128 станциях (рис. 1) ГНСС-сетей IGS [10] и CORS [7]. Продолжительность записей составила от 10 до 13 суток. Данные измерений на всех станциях не содержат пропусков более 15 минут. В целом выбранные станции имеют достаточно равномерное пространственное распределение, со сгущением на территории США и с некоторым недостатком станций на Азиатском континенте и в Антарктиде (т.к. данные многих станций там содержали значительные пропуски или имели шаг дискретизации более 1 с). Данные ГНСС-измерений станций сетей IGS и CORS доступны на официальных сайтах [12, 7].
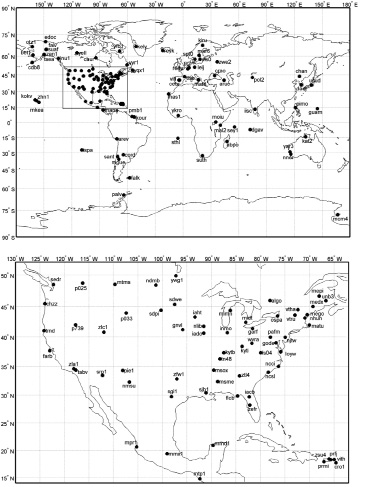
Рис. 1. ГНСС-станции, использованные для построения моделей шума
Для упрощения работы с данными реальных ГНСС-наблюдений, инструментальные данные за выбранный временной интервал и необходимая сопутствующая информация сначала накапливались в специальном архиве, после чего проводилась их обработка путем имитации вычислений в режиме реального времени. Обработка была осуществлена в известной программе BKG Ntrip Client [3] с использованием поправок часов и орбит спутников CLK91, предоставляемых сервисом BKG.
Для уменьшения влияния ошибок, связанных с переотражением спутникового сигнала от препятствий и подстилающей поверхности, к получаемым рядам координат применялась сидерическая фильтрация [6]. Фильтрованный сигнал (по каждой компоненте) рассчитывался по следующей формуле:
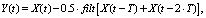
где X(t) – исходный сигнал; Y(t) – фильтрованный сигнал; оператор filt[ ] обозначает линейную полосовую фильтрацию сигнала; T – период повторения взаимного расположения навигационных спутников и приемной антенны, установленной в определяемом пункте.
Длительность сигнала после применения сидерической фильтрации уменьшается на 2·T. Период T был определен автокорреляцией рядов координат и составил для большинства станций 86154 или 86155 с.
Границы частотного диапазона для фильтрации определялись вручную индивидуально для каждой станции, охватывая только тот диапазон периодов, в котором происходило уменьшение уровня шума. На нескольких станциях сидерическая фильтрация не приводила к понижению уровня шума и поэтому не применялась.
Методика определения спектральной плотности мощности (СПМ) основана на алгоритме Уэлча и была максимально приближена к той, которая использовалась в работе [5]. Весь ряд координат по каждой компоненте каждой станции разбивался на сегменты длиной 43200 отсчетов. Соседние сегменты были сдвинуты друг относительно друга на 8640 отсчетов (на 20 %). Сегменты с более чем 120 пропущенными отсчетами отбрасывались, меньшие пропуски заполнялись линейной интерполяцией.
В каждом сегменте исключался линейный тренд и применялась оконная функция Ханна, после чего рассчитывалась СПМ. Полученные кривые СПМ усреднялись скользящим средним с шириной в одну октаву, т.е. для некоторого периода T усреднялись все значения СМП, попадающие в диапазон от T·2-½ до T·2½. В качестве итоговых значений были взяты восемь точек на октаву, т.е. периоды двух соседних точек отличались в 21/8 раз. Максимальный период был ограничен значением 10000 с.
Таким образом, для каждого сегмента были определены 95 значений СПМ, соответствующие средним значениям периодов от 2,83 до 10000 с. Общее количество полученных сегментов со всех станций составило 9059, таким образом, для каждого периода была получена выборка из 9059 значений СПМ. В этих выборках определялись значения СПМ, соответствующие уровням вероятности 5 %, 50 % и 95 %, аппроксимацией которых были построены следующие модели шума в рядах координат, полученных обработкой данных ГНСС-измерений в режиме реального времени методом PPP:
1. LRTGNM (Low Real-Time GNSS Noise Models) – модель низкого (5 %) шума.
2. MRTGNM (Median Real-Time GNSS Noise Models) – модель медианного (50 %) шума.
3. HRTGNM (High Real-Time GNSS Noise Models) – модель высокого (95 %) шума.
Каждая из указанных моделей построена отдельно для горизонтальных компонент (к названию добавляется нижний индекс NE, например, MRTGNMNE) и отдельно для вертикальной компоненты (нижний индекс UD, например MRTGNMUD).
Результаты исследования и их обсуждение
Построенные модели аналитически выражаются через набор опорных точек, для которых заданы значения периода и СПМ, приведенные в таблице.
Полученные модели низкого (LRTGNM), медианного (MRTGNM) и высокого (HRTGNM) шума
|
Период, с |
Уровень шума, дБ относительно 1 м2/Гц |
|||||
|
Горизонтальные компоненты |
Вертикальная компонента |
|||||
|
LRTGNMNE |
MRTGNMNE |
HRTGNMNE |
LRTGNMUD |
MRTGNMUD |
HRTGNMUD |
|
|
2,83 |
– 57 |
– 53,5 |
– 47,5 |
– 48,5 |
– 45,5 |
– 39 |
|
6 |
– 51,5 |
– 49 |
– 45 |
– 43,5 |
– 41,5 |
– |
|
8 |
– 52 |
– 48,5 |
– 44,5 |
– 44 |
– 41 |
– 36,5 |
|
20 |
– |
– |
– |
– |
– |
– 32 |
|
30 |
– 46 |
– 42,5 |
– 37,5 |
– 38 |
– 35,5 |
– 28,5 |
|
70 |
– |
– |
– |
– |
– |
– 25 |
|
400 |
– 32,5 |
– 27,5 |
– 22 |
– 25 |
– 20 |
– 14,5 |
|
2000 |
– |
– |
– |
– 17 |
– 11,5 |
– 4 |
|
3000 |
– 22 |
– 16 |
– 9 |
– |
– |
– |
|
10000 |
– 13 |
– 4,5 |
2,5 |
– 5 |
4 |
11 |
Для произвольного периода T значение СПМ P может быть определено линейной интерполяцией при логарифмическом масштабе периодов:
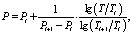
где Ti и Ti+1 – периоды соседних опорных точек (Тi ≤ Т ≤ Тi+1); Pi и Pi+1 – соответствующие им значения СПМ.
При необходимости модели шума могут также задаваться в скоростях и ускорениях:
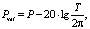
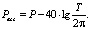
Полученные результаты моделирования шума рядов ГНСС-координат могут быть использованы для сравнения точности регистрации колебаний земной поверхности при помощи ГНСС и сейсмических приборов (широкополосными сейсмометрами и акселерометрами). На рис. 2 приведено сравнение построенных моделей шума с моделями сейсмического шума NHNM (New High Noise Model) и NLNM (New Low Noise Model) для широкополосных сейсмометров [13] и с моделями шума высокоточных акселерометров AHNM (accelerometric high noise model) и ALNM (accelerometric low noise model) [5].
В диапазоне периодов от 3 до 1000 с модели MRTGNM значительно выше моделей сейсмического шума NLNM и NHNM. При дальнейшем увеличении периода разница между ними уменьшается, т.е. чувствительность ГНСС-приемника и широкополосных сейсмометров становится сопоставимой. Модели шума для акселерометров ALNM и AHNM построены только для периодов до 150 с, они также значительно ниже моделей MRTGNM. Если провести экстраполяцию моделей ALNM и AHNM на более длинные периоды, то на периодах 300–2000 с эти модели были бы сопоставимы с моделями MRTGNM, а на периодах более 2000 с, по-видимому, чувствительность ГНСС-приемника значительно превосходит чувствительность высокоточных акселерометров.
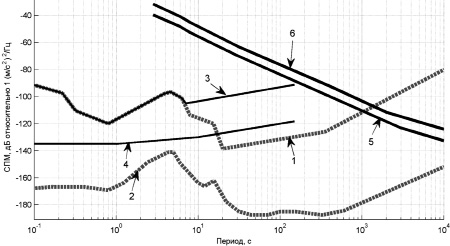
Рис. 2. Сравнение построенных моделей и моделей сейсмического шума: 1 и 2 – модели высокого (NHNM) и низкого (NLNM) сейсмического шума [13]; 3 и 4 – модели высокого (AHNM) и низкого (ALNM) шума высокоточных акселерометров [5]; 5 и 6 – построенные модели MRTGNMNE и MRTGNMUD
Таким образом, полученные результаты доказывают нецелесообразность замены «стандартных» сейсмических приборов (широкополосных сейсмических станций и высокоточных акселерометров) ГНСС-приемниками, вопреки ожиданиям некоторых исследователей [9]. Однако для получения более полного спектра сейсмических колебаний объединение записей сейсмического и ГНСС-оборудования [8] вполне оправдано, т.к. только спутниковые приемники в состоянии зарегистрировать сейсмические волны с периодами выше тысячи секунд и статические смещения.
Построенные модели шума рядов ГНСС-координат также позволяют оценить применимость ГНСС для регистрации сейсмических колебаний в заданном районе от определенного типа землетрясений. Для этого необходимо рассчитать реальные или теоретические (прогнозные) спектры сейсмических колебаний и сравнить их с моделями шума.
Исследования выполнены в рамках государственного задания Института тектоники и геофизики им. Ю.А. Косыгина ДВО РАН и при частичном финансировании РФФИ (проекты 16-05-00097a (Пупатенко В.В.), 17-55-53110 (Шестаков Н.В.), 17-55-50030 (Шестаков Н.В.).
Библиографическая ссылка
Пупатенко В.В., Шестаков Н.В. МОДЕЛИРОВАНИЕ ШУМА В РЯДАХ ВЫСОКОЧАСТОТНЫХ ГНСС-КООРДИНАТ, ПОЛУЧАЕМЫХ В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ // Успехи современного естествознания. 2017. № 2. С. 140-144;URL: https://natural-sciences.ru/ru/article/view?id=36376 (дата обращения: 14.02.2026).



