Большинство молекулярных структур рассмотрено методом валентных связей, описывающим конфигурацию молекул с точки зрения направленности атомных орбиталей [1]. В последнее время значительное внимание уделено методу молекулярных орбиталей, согласно которому электроны в молекуле занимают орбитали, охватывающие всю молекулу.
Целью работы является разработка комплексного метода определения валентного угла трехатомных водородосодержащих молекул, находящихся в устойчивом состоянии на основе данных инфракрасных спектров.
Молекула воды является симметричной и относится к точечной группе C2ν с двумя зеркальными плоскостями симметрии и двукратной осью вращения. Для определения валентного угла в молекуле H2O необходимо построить ее геометрическую модель. Для этого построим в пространстве плоскость E1 и проведем нормаль n, которая в свою очередь будет принадлежать плоскости Е2. В точке пересечения нормали и плоскости Е1 разместим центр массы (ЦМ) атома кислорода. Зафиксируем данную точку как точку О. Проведем в плоскости E1 вектор R и совместим его начало с точкой О. Проведем через данный вектор ось абсцисс.
Путем вращения вектора R вокруг нормали n получаем окружность с радиусом R. На данной окружности произвольно выбираем две точки 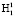 и
и 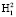 , как показано на рис. 1. Точка О является центром масс атома кислорода и совмещена с началом координат. Точки H1 и H2 являются однотипными точками (атомы водорода), при этом H1 – вершина вектора R, а положение точки H2 выбирается на окружности произвольно. Предлагаемая идея расчета валентного угла заключается в построении двух геометрических фигур: прямоугольника PH1K2H2, задача которого управлять величиной валентного угла ∠H1OH2 с помощью диагонали PK2, и прямоугольника PH1OK1, задача которого управлять координатами точек H1 и H2 относительно точки О с помощью диагонали прямоугольника РO. Таким образом, валентный угол a молекулы H2O представляет собой угол H1OH2. Для определения величины валентного угла из точки H2 проведем линию параллельно линии ОH1 и опустим на нее перпендикуляр из точки H1. Точку пересечения этих двух линий обозначим буквой Р, координаты которой потребуются для формирования математической модели при вычислении валентного угла. Если валентный угол выбрать как угол, равный 90 °, то установится подобие двух фигур, а именно PH1OK1 и PH1K2H2 с одной общей диагональю РО. Отношение диагонали РК2 прямоугольника PH1K2H2 к диагонали РО квадрата PH1OK1 обозначим через коэффициент симметрии эквивалентных координат:
, как показано на рис. 1. Точка О является центром масс атома кислорода и совмещена с началом координат. Точки H1 и H2 являются однотипными точками (атомы водорода), при этом H1 – вершина вектора R, а положение точки H2 выбирается на окружности произвольно. Предлагаемая идея расчета валентного угла заключается в построении двух геометрических фигур: прямоугольника PH1K2H2, задача которого управлять величиной валентного угла ∠H1OH2 с помощью диагонали PK2, и прямоугольника PH1OK1, задача которого управлять координатами точек H1 и H2 относительно точки О с помощью диагонали прямоугольника РO. Таким образом, валентный угол a молекулы H2O представляет собой угол H1OH2. Для определения величины валентного угла из точки H2 проведем линию параллельно линии ОH1 и опустим на нее перпендикуляр из точки H1. Точку пересечения этих двух линий обозначим буквой Р, координаты которой потребуются для формирования математической модели при вычислении валентного угла. Если валентный угол выбрать как угол, равный 90 °, то установится подобие двух фигур, а именно PH1OK1 и PH1K2H2 с одной общей диагональю РО. Отношение диагонали РК2 прямоугольника PH1K2H2 к диагонали РО квадрата PH1OK1 обозначим через коэффициент симметрии эквивалентных координат:
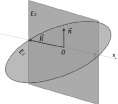
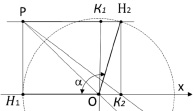
Рис. 1. Образование геометрической модели молекулы H2O (слева) и геометрическая модель валентного угла молекулы H2O (справа)
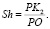 (1)
(1)
При значении угла a, равном 90 градусов, коэффициент Sh = 1. При этом условии координаты точек H1 и H2 переходят друг в друга при операциях симметрии. Коэффициент Sh также можно определить из отношения валентного угла a к углу 90 °
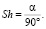 (2)
(2)
По условию задачи валентный угол a неизвестен. С помощью вращения вектора R вокруг нормали получим множество точек, равноудаленных от центра О. Воспользовавшись формулой (2), построим табл. 1 значений коэффициента Sh для различных валентных углов.
Таблица 1
Коэффициент симметрии при различных валентных углах
|
Валентный угол α |
Коэффициент Sh |
Валентный угол α |
Коэффициент Sh |
|
90 |
1,0 |
104 |
1,155 |
|
100 |
1,111 |
105 |
1,166 |
|
102 |
1,133 |
106 |
1,177 |
Согласно уравнению (1) коэффициента симметрии определяется через отношение двух отрезков (диапазонов). Изменение значений колебательных частот водорода в составе жидкой молекулы воды и электронных колебаний молекулы водорода H2 представим разностью этих частот, как диапазон. Прецессия суммарного наведённого орбитального магнитного момента молекулы воды в инфракрасном спектре отражает колебательные частоты как целой молекулы вокруг вектора магнитной индукции внешнего поля и является результирующей двух прецессий. Прецессии от общего наведённого орбитального магнитного момента первого атома и второго атома водорода молекулы воды. Прецессия суммарного наведённого орбитального магнитного момента молекулы воды в инфракрасном спектре отражает колебательные частоты молекулы, состоящей из разных атомов и меняется с изменением расстояния между центрами масс ядер около их равновесного положения. Частота вращательного движения молекулы воды определяется как вращение целой молекулы вокруг оси симметрии. Таким образом, и колебательные, и вращательные частоты связаны с амплитудой общего наведённого орбитального магнитного момента молекулы воды и индуцированного дипольного момента, в инфракрасном спектре излучения.
Результаты исследования и их обсуждение
Инфракрасный спектр жидкой воды по линии водорода выражен колебательными частотами 3657 и 3756 см-1 [2, 3], о чем свидетельствует широкий спектр в данном диапазоне (рис. 2), излучаемый атомами водорода молекулы жидкой воды.
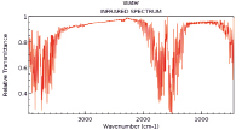
Рис. 2. Инфракрасный спектр жидкой воды [4]
Для построения гипотетической модели валентного угла одиночной молекулы Н2О как нелинейной и симметричной воспользуемся данными колебательных и вращательных констант для нормальных электронных состояний трехатомных молекул [2, 3] (табл. 2).
Таблица 2
Колебательные и вращательные константы для нормальных электронных состояний жидкой молекулы воды в инфракрасном спектре излучения
|
Молекула |
Длина валентной связи, пм |
Колебательная частота, ω (см-1) |
|
H2O |
О- |
3756 |
|
О- |
3657 |
|
|
O2 |
1595 |
Для удобства отобразим данные колебательных частот в виде вертикальных полос, аналогично полосатым спектрам излучения для двухатомных и трехатомных молекул (рис. 3).
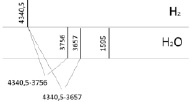
Рис. 3. Определение диапазона спектра прецессии вектора общего наведённого орбитального магнитного момента в инфракрасном спектре в молекуле жидкой воды и электронной частоты двухатомной молекулы водорода в ультрафиолетовом спектре
Молекула водорода как самостоятельная молекула идентифицируется по ультрафиолетовому спектру электронного излучения с колебательной частотой, равной 4340,5см-1 для состояния 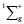 . Состояние
. Состояние 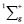 имеет потенциальную кривую с глубоким минимумом потенциальной энергии и является устойчивым состоянием. Данное значение отобразим вертикальной полосой в верхнем ряду электронных колебательных частот атома водорода. Значения колебательных частот молекулы жидкой воды, полученных в инфракрасном спектре излучения, отобразим в нижнем ряду. Изменение значения колебательных частот водорода в составе жидкой молекулы воды и электронных колебаний молекулы водорода H2 представим разностью этих частот, как диапазон. Диапазон частот между метками в инфракрасном и ультрафиолетовом излучении определим как разность. Метками в инфракрасном спектре являются колебательные частоты одиночной молекулы воды 3756 см-1 и 3657 см-1, метками в ультрафиолетовом излучении является электронная частота молекулы водорода 4340,5 см-1. Таким образом, диапазон частот между метками ультрафиолетового и инфракрасного излучения показывает, как меняется частота молекулы водорода после того, как она вступила в связь с атомом кислорода для образования молекулы воды. Согласно выражению полной энергии, в каждом устойчивом электронном состоянии молекула может иметь и колебательную энергию относительно положения равновесия, и вращательную энергию. Е = Еэ + Екол + Евр. Испускаемую или поглощаемую частоту молекулы можно рассмотреть как сумму составных частей V = Vэ + Vкол + Vвр. Таким образом разность между электронной частотой и колебательной при Vвр = 0 определяет длину диапазона спектра прецессии вектора общего наведённого орбитального магнитного момента молекулы воды как целого. Молекула воды содержит два атома водорода, следовательно, прецессия общего наведённого орбитального магнитного момента О-
имеет потенциальную кривую с глубоким минимумом потенциальной энергии и является устойчивым состоянием. Данное значение отобразим вертикальной полосой в верхнем ряду электронных колебательных частот атома водорода. Значения колебательных частот молекулы жидкой воды, полученных в инфракрасном спектре излучения, отобразим в нижнем ряду. Изменение значения колебательных частот водорода в составе жидкой молекулы воды и электронных колебаний молекулы водорода H2 представим разностью этих частот, как диапазон. Диапазон частот между метками в инфракрасном и ультрафиолетовом излучении определим как разность. Метками в инфракрасном спектре являются колебательные частоты одиночной молекулы воды 3756 см-1 и 3657 см-1, метками в ультрафиолетовом излучении является электронная частота молекулы водорода 4340,5 см-1. Таким образом, диапазон частот между метками ультрафиолетового и инфракрасного излучения показывает, как меняется частота молекулы водорода после того, как она вступила в связь с атомом кислорода для образования молекулы воды. Согласно выражению полной энергии, в каждом устойчивом электронном состоянии молекула может иметь и колебательную энергию относительно положения равновесия, и вращательную энергию. Е = Еэ + Екол + Евр. Испускаемую или поглощаемую частоту молекулы можно рассмотреть как сумму составных частей V = Vэ + Vкол + Vвр. Таким образом разность между электронной частотой и колебательной при Vвр = 0 определяет длину диапазона спектра прецессии вектора общего наведённого орбитального магнитного момента молекулы воды как целого. Молекула воды содержит два атома водорода, следовательно, прецессия общего наведённого орбитального магнитного момента О-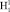 и О-
и О-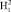 для такой молекулы воды как целого состоит из двух частей. Для молекулы водорода, которая состоит из двух одинаковых атомов, диполь отсутствует, поэтому излучение в инфракрасном спектре тоже отсутствует.
для такой молекулы воды как целого состоит из двух частей. Для молекулы водорода, которая состоит из двух одинаковых атомов, диполь отсутствует, поэтому излучение в инфракрасном спектре тоже отсутствует.
Для вычисления валентного угла по данным спектра излучения колебательных частот в инфракрасном диапазоне представим значения электронной частоты молекулы водорода, и атомов водорода, входящих в состав воды и атома кислорода в одном ряду (рис. 4).
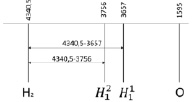
Рис. 4. Определение диапазона спектра прецессии вектора общего наведённого орбитального магнитного момента в инфракрасном спектре в молекуле жидкой воды и электронной частоты двухатомной молекулы водорода в ультрафиолетовом спектре
Согласно уравнению (1) определение коэффициента симметрии осуществляется через отношения двух отрезков (диапазонов). В качестве числителя используется диапазон между частотой индуцированного общего наведённого орбитального магнитного момента О-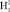 и колебательной частотой нормального электронного состояния молекулы водорода. В качестве знаменателя используется диапазон между частотой индуцированного общего наведённого орбитального магнитного момента О-
и колебательной частотой нормального электронного состояния молекулы водорода. В качестве знаменателя используется диапазон между частотой индуцированного общего наведённого орбитального магнитного момента О-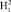 и колебательной частотой нормального электронного состояния молекулы водорода. Уравнение коэффициента симметрии эквивалентных координат представлено в виде
и колебательной частотой нормального электронного состояния молекулы водорода. Уравнение коэффициента симметрии эквивалентных координат представлено в виде
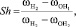 (3)
(3)
где в ультрафиолетовом спектре 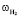 – колебательная частота нормального электронного состояния атома водорода Н2, см-1; в инфракрасном спектре
– колебательная частота нормального электронного состояния атома водорода Н2, см-1; в инфракрасном спектре 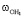 – колебательная частота первого атома водорода молекулы воды, см-1;
– колебательная частота первого атома водорода молекулы воды, см-1; 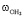 – колебательная частота второго атома водорода молекулы воды, см-1. Согласно уравнению (2) связь коэффициента Sh и валентного угла определяется углом 90 °:
– колебательная частота второго атома водорода молекулы воды, см-1. Согласно уравнению (2) связь коэффициента Sh и валентного угла определяется углом 90 °:
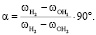 (4)
(4)
Подставив значения колебательных частот, получим
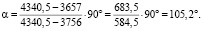
Диапазон прецессии между метками для диполя О-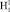 составляет 683,5 см-1, а для диполя
составляет 683,5 см-1, а для диполя 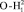 составляет 584,5 см-1. Полученное значение валентного угла соответствует значению коэффициента эквивалентных координат Sh = 1,169. Коэффициент полученный в результате этого отношения, определяет валентный угол жидкой воды по спектру излучения колебательных частот в инфракрасном диапазоне согласно выражению (3).
составляет 584,5 см-1. Полученное значение валентного угла соответствует значению коэффициента эквивалентных координат Sh = 1,169. Коэффициент полученный в результате этого отношения, определяет валентный угол жидкой воды по спектру излучения колебательных частот в инфракрасном диапазоне согласно выражению (3).
Данные валентного угла водородосодержащих молекул, полученные с помощью выражения (4), представлены в табл. 3 и хорошо согласуются с известными результатами расчета валентного угла [5].
Таблица 3
Колебательные частоты водородосодержащих молекул
|
Молекула |
Колебательная частота, ω (см-1) |
Валентный угол, α* |
|
SH2 |
2611 и 2684 |
93,96 ° |
|
SeH2 |
2260 и 2350 |
94,07 ° |
|
HOD |
3707,5 и 2723,7 |
92,4 ° |
Примечание. *при условии взаимности фундаментальных колебаний WHO/WDO = 1,355.
Физический смысл показателя коэффициента симметрии эквивалентных координат Sh заключается в том, что он определяет, на сколько диапазон прецессии индуцированного общего наведённого орбитального магнитного момента первого атома водорода молекулы воды отличается от диапазона прецессии индуцированного общего наведённого орбитального магнитного момента второго атома водорода согласно меткам в ультрафиолетовом и инфракрасном спектре излучения. А также, как далеко друг от друга расположены центры масс атомов водорода в трехатомных водородосодержащих молекулах и тем самым выражает амплитуду деформационного колебания, как результат изменения межъядерного расстояния между центром масс атома кислорода и центром масс атома водорода.
Математическая модель валентного угла одиночной молекулы жидкой воды
Для определения точки P геометрической модели построим математическую модель молекулы жидкой воды в системе координат колебательной частоты ω и длины ковалентной связи R. Межъядерное расстояние 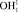 составляет 110,26 пм. Центр масс атома кислорода совмещен с началом координат согласно рис. 5. В нашей математической модели центр масс молекулы водорода в цепочке
составляет 110,26 пм. Центр масс атома кислорода совмещен с началом координат согласно рис. 5. В нашей математической модели центр масс молекулы водорода в цепочке 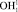 находится в точке Х2. Водород цепочки
находится в точке Х2. Водород цепочки 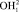 поместим в точку Х1 на расстоянии 95,8 пм от начала координат. Перенесем геометрическую модель (рис. 1) в данную систему координат ω-R. Из рис. 5 видно, что точка Х1 принадлежит прямоугольнику РК1Х1ХР , а Х2 прямоугольнику PK2X2Xp. Обозначим значения спектров водородов на оси ординат и соединим их с точками X1 и X2. Точку пересечения полученных линий обозначим через P, координаты которой определяют значение валентного угла.
поместим в точку Х1 на расстоянии 95,8 пм от начала координат. Перенесем геометрическую модель (рис. 1) в данную систему координат ω-R. Из рис. 5 видно, что точка Х1 принадлежит прямоугольнику РК1Х1ХР , а Х2 прямоугольнику PK2X2Xp. Обозначим значения спектров водородов на оси ординат и соединим их с точками X1 и X2. Точку пересечения полученных линий обозначим через P, координаты которой определяют значение валентного угла.
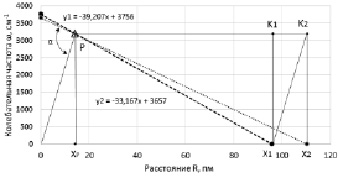
Рис. 5. Молекула водорода Н2 и ОН в системе координат ω-R, с точкой пересечения P(Δ)
Валентный угол в соответствии с выражением (1) составляет 105,2 °, и определяется через коэффициент симметрии эквивалентных координат. На рис. 5 представлены две диагонали РХ1 и РХ2 двух прямоугольников, которые определяют угол между прямой ОХ1К2. Система линейных уравнений, составленной из у1 и у2, при совместном решении определяет точку пересечения, обозначенной буквой Р. Точка Р симметричная относительно оси ординат и является балансной между колебательной частотой и длиной валентной связи.
Заключение
На основании предложенной идеи расчета валентного угла получена геометрическая модель молекулы жидкой воды с двумя колебательными системами, характеризующимися диагоналями PK2 и РО (рис. 3). С помощью разработанной методики проведена расшифровка инфракрасного спектра жидкой воды на предмет определения валентного угла. Полученное выражение для определения значения валентного угла базируется на основе представленной геометрической модели молекулы жидкой воды, состоящей из двух колебательных систем, и выраженной как диапазон между частотой индуцированного общего наведённого орбитального магнитного момента молекулы воды и электронной частотой атома водорода. Полученные значения валентных углов для жидкой воды и водородосодержащих молекул хорошо согласуются с известными результатами. Спектр молекулы водорода Н2 в нормальном электронном состоянии имеет электронную частоту 4340,5 см-1. Состояние  имеет потенциальную кривую с глубоким минимумом потенциальной энергии, что является необходимым условием при выборе электронной частоты и при определении валентного угла трехатомных водородосодержащих молекул, находящихся в устойчивом состоянии. Таким образом, диапазон частот между метками ультрафиолетового и инфракрасного излучения показывает, как меняется частота молекулы водорода после того, как она вступила в связь с молекулой кислорода для образования молекулы воды.
имеет потенциальную кривую с глубоким минимумом потенциальной энергии, что является необходимым условием при выборе электронной частоты и при определении валентного угла трехатомных водородосодержащих молекул, находящихся в устойчивом состоянии. Таким образом, диапазон частот между метками ультрафиолетового и инфракрасного излучения показывает, как меняется частота молекулы водорода после того, как она вступила в связь с молекулой кислорода для образования молекулы воды.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-38-00448.
Библиографическая ссылка
Шорсткий И.А. МЕТОД ОПРЕДЕЛЕНИЯ ВАЛЕНТНОГО УГЛА ОДИНОЧНОЙ МОЛЕКУЛЫ ЖИДКОЙ ВОДЫ ЧЕРЕЗ ИНФРАКРАСНЫЙ СПЕКТР ИЗЛУЧЕНИЯ // Успехи современного естествознания. 2018. № 10. С. 28-33;URL: https://natural-sciences.ru/ru/article/view?id=36877 (дата обращения: 04.03.2026).




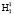 95,8
95,8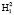 95,8
95,8