Методика определения механических свойств пород и грунтов должна в определенном виде учитывать геологический состав горной породы на любой глубине, так как состав породы обычно обладает большим разнообразием и разбросом свойств компонент породы по механическим характеристикам. Поэтому в настоящее время общепринятым является описание механических свойств пород и грунтов как квазиизотропных, т.е. сред изотропных в среднем. Обоснованием этого заключения является прямая аналогия между структурой горной породы или почвы и структурой композиционных материалов [1].
Однако, несмотря на это уже устоявшееся представление о механике горных пород, как одного из вариантов механики композиционных материалов, на текущий момент не существует четких рекомендаций по использованию тех или иных методик оценки средних механических характеристик представительного объема породы или грунта по их составу. Это связано прежде всего с тем, что до недавнего времени попросту не было создано даже удовлетворительного математического аппарата теоретического усреднения свойств многокомпонентных смесей. Только после появления основополагающих работ [2, 3], которые довели до логического конца методику Хилла, основанную на оценках Фойгта и Рейсса, стало возможно говорить о создании целостной инженерной методики, как расчетного прогнозирования эффективных свойств горных массивов и почв, так и обоснованного применения этих усреднений в расчетах в геомеханике.
Разработанная в рамках проекта программы союзного государства «Недра» методика позволит отказаться от испытаний горной породы для выяснения механических характеристик, а ограничиться выяснением объемных долей компонент, присутствующих в породе (сухих песка, глины, камня, органических включений и отдельно объема воды) по результатам бурения. Используя механические характеристики каждой из компонент в отдельности, можно будет по результатам определения их объемных долей вычислить прогнозируемые физические значения. В связи с разнообразием свойств перечисленных компонент на этом этапе создания модели следует ограничиться линейным квазиупругим приближением уравнения состояния как грунта или породы, так и их компонент, предполагая, что даже вода является упругой и ее коэффициент Пуассона ориентировочно равен 0,45.
Впервые в рамках предложенной методики предлагается использовать структурно-феноменологический подход, основанный на построении иерархической модели усреднения механических характеристик, используемых их для расчета НДС различных по размеру фрагментов земной толщи. Так для расчета оседаний дневной поверхности необходимо усреднять механические характеристики по всему объему толщи породы над выработкой, а для расчета НДС слоя соли над выработкой для повышения точности расчета целесообразно выполнять усреднение механических характеристик исключительно по геологическому составу солевого пласта с заменой веса породы над выделенным фрагментом солевого пласта соответствующей распределенной нагрузкой.
Предлагаемая авторами методика является обобщением уже известных результатов, полученных в работах [4–6], где по факту продемонстрирован метод определения эффективных квазиизотропных характеристик всего горного массива над выработкой по результатам обсчета измеренных вертикальных сдвижений существующего объекта без определения концентраций компонент на разных горизонтах.
В рамках построения общей теории квазиупругого поведения горных пород, при анализе литературных источников был установлено [4–6], что эффективный модуль сдвига для горного массива не является вычисляемой величиной через эффективные модуль упругости и коэффициент Пуассона, а требует отдельного определения для достижения необходимой точности совпадения расчетных величин оседания поверхности с экспериментально полученными на уже существующих объектах.
Например, при усреднении механических характеристик всей массы горной породы для определения сдвижения дневной поверхности (самой иерархически крупной модели) будем исходить из закона Кулона – Мора, определяющего пластическое поведение материала горной породы на поверхностях пластического сдвига [7, 8]:
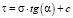 ,
,
где τ, σ – величины касательных и нормальных напряжений, α – угол внутреннего трения, с – сцепление.
Приняв, что в толще породы, удаленной как от поверхности, так и от выработки, исследователь имеет дело с одноосным напряженным состоянием, создаваемым силой тяжести породы, выделим ромбовидный элемент (рис. 1). Можно утверждать, что касательные напряжения, действующие на границе выделенного ромбовидного элемента (рис. 1), ориентированного вдоль направления первого главного напряжения (единственного отличного от нуля напряжения, действующего в толще), с достаточной точностью не зависят от деформаций, изменяющих углы при вершинах указанного элемента (рис. 1), а следовательно, не зависят от деформаций сдвига. В вычислительном смысле это означает, что для самой иерархически крупной модели следует уменьшить значение эффективного модуля сдвига ⟨G⟩ для всей толщи до незначительной по сравнением с отношением 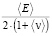 (где ⟨E⟩ – эффективного модуля Юнга, ⟨ν⟩ – эффективный коэффициент Пуассона), например до 5 % от отношения
(где ⟨E⟩ – эффективного модуля Юнга, ⟨ν⟩ – эффективный коэффициент Пуассона), например до 5 % от отношения 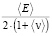 (но не более 10 %, как это установлено в [4–6]).
(но не более 10 %, как это установлено в [4–6]).
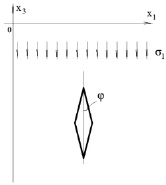
Рис. 1. Выделение ромбовидного элемента горной породы в области однородного распределения напряжений, которая удалена как от дневной поверхности, так и от выработки
Поэтому, на взгляд авторов, получивших аналогичные результаты для расчетов сдвижения дневной поверхности для существующей горизонтальной выработки на Солигорском месторождении, в общую методику решения геомеханических задач необходимо внести существенные изменения в отличие от машиностроения:
− либо при вычислении сдвижения дневной поверхности (иерархически самой крупной модели) считать, что эффективный модуль сдвига всей толщи породы малой величиной по сравнению с эффективным модулем Юнга;
− либо в случае иерархического моделирования относительно малого фрагмента горной породы (например, вокруг выработки) считать эффективный модуль сдвига породы или почвы величиной независимо определяемой из экспериментальных данных наравне с эффективным модулем Юрга и коэффициентом Пуассона;
− использовать для расчетов напряженного состояния горного массива и/или почвы с помощью стандартного программного обеспечения эффективную ортотропную модель с тремя одинаковыми эффективными модулями по всем направлениям, т.е. в этой модели эффективные модули Юнга, сдвига и коэффициент Пуассона являются независимо определяемыми, но одинаковыми величинами для всех трех направлений.
В связи с этим в известную методику определения эффективных характеристик композиционных сред [2, 3] внесены упрощения, позволяющие как довести методику до инженерного уровня, не сильно потеряв в точности определения механических характеристик горного массива, так и использовать ее для определения трех независимых упругих характеристик горных массивов – эффективных модуля Юнга, модуля сдвига и коэффициента Пуассона.
На основе разработанной авторами методики [2, 3] в данной статье выведены уравнения Ламе динамики горного массива для решения задач в смысле средних по представительному объему породы напряжений и перемещений. Установлено, что теоретическое определение эффективной скорости распространения волны в горном массиве существенно зависит от всех трех параметров (эффективных модуля Юнга, модуля сдвига и коэффициента Пуассона).
Геометрические предположения
Данная работа полностью опирается на аналогию между горной породой или грунтом и композиционным в среднем изотропным телом, так как композиционный материал с зернистой структурой полностью соответствует составу грунта или горной породы в Беларуси. Именно поэтому в основе данного исследования лежат результаты авторов, полученные для композиционных тел и сред [2, 3]. Основным отличием данной работы является использование результатов линеаризации нелинейной диаграммы деформирования компонент горной породы или грунта, а также упрощенное приближение эффективных механических характеристик горных пород и грунтов с использованием приближения Хилла, которое, как установлено авторами, также является достаточно точным относительно приближения Кравчука – Тарасюка [2, 3].
Рассмотрим пространственную декартову систему координат с осями 0xi (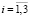 ). Предполагается, что горная порода или грунт занимает объем V, а точка
). Предполагается, что горная порода или грунт занимает объем V, а точка 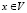 имеет три координаты
имеет три координаты 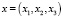 . Через функцию
. Через функцию 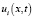 (
(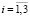 ) обозначим перемещения точки x горной породы или грунта вдоль соответствующей оси 0xi (проекцию на указанное направление) в момент времени t. Отметим, что при выводе всех уравнений геомеханики исследователь использует для произвольной точки
) обозначим перемещения точки x горной породы или грунта вдоль соответствующей оси 0xi (проекцию на указанное направление) в момент времени t. Отметим, что при выводе всех уравнений геомеханики исследователь использует для произвольной точки 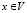 описанный вокруг нее элементарный объем
описанный вокруг нее элементарный объем 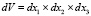 (где dxi – приращение вдоль оси 0xi).
(где dxi – приращение вдоль оси 0xi).
Линеаризация диаграммы деформирования
Предполагается, что известна наибольшая деформация горной породы или грунта εпр, исходя из предварительных оценочных расчетов. Таким образом, задан отрезок [0, εпр] на оси деформации. Тогда нелинейное поведение fk каждой компоненты породы или грунта с номером k (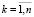 , где n – количество установленных компонент) при деформации на отрезке [0, εпр] приближается линейной функцией с секущим модулем (рис. 2).
, где n – количество установленных компонент) при деформации на отрезке [0, εпр] приближается линейной функцией с секущим модулем (рис. 2).
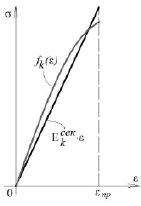
Рис. 2. Линеаризация нелинейного поведения грунта
Таким образом, предполагается, что к началу применения данной методики уже определены все секущие модули 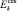 компонент породы или грунта, а также определены их коэффициенты Пуассона vk и модуль сдвига
компонент породы или грунта, а также определены их коэффициенты Пуассона vk и модуль сдвига 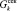 .
.
Особенности вывода уравнений для горной породы с использованием объемных долей компонент
Будем называть представительным объемом горной породы наименьший объем, в котором физические характеристики остаются в среднем равными физическим характеристикам всего объема горного массива.
В отличие от сплошной среды уравнения не будут верны непосредственно при предельном переходе dV → 0, так как в предлагаемой теории деформирования горных пород представительный объем горной породы dV ≠ 0. Но, с другой стороны, он бесконечно мал по сравнению со всем исследуемым объемом V. Точнее, 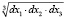 (характерный размер представительного объема) мал по сравнению с наименьшим характерным объемом фрагмента горного массива. Отметим, что во всем объеме гороного массива и в элементарном представительном объеме dV концентрации компонент (объемные доли) равны γk (где k (
(характерный размер представительного объема) мал по сравнению с наименьшим характерным объемом фрагмента горного массива. Отметим, что во всем объеме гороного массива и в элементарном представительном объеме dV концентрации компонент (объемные доли) равны γk (где k (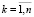 ) – номер компоненты, при этом выполнено условие нормировки
) – номер компоненты, при этом выполнено условие нормировки 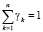 ). Представительный dV объем горной породы будем называть макроточкой.
). Представительный dV объем горной породы будем называть макроточкой.
Очевидно, что для каждой компоненты представительного объема неоднородного многокомпонентного твердого тела должны быть известны ее плотность ρk, модуль Юнга 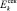 , коэффициент Пуассона vk, модулем сдвига
, коэффициент Пуассона vk, модулем сдвига 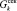 .
.
При использовании данных гипотез план вывода уравнений для геомеханических объектов полностью сохраняется с точностью до замены понятия элементарного объема на представительный объем.
Отметим также, что в смысле формулировки объемных долей γk их следует рассматривать также как дискретную случайную величину присутствия компоненты породы или грунта с номером k в точке 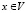 .
.
Обозначим через 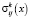 и
и 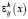 (
(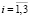 ,
, 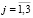 ) дискретные значения напряжений и деформаций на k-й компоненте горного массива в представительном объеме. Домножая на γk и суммируя по k, получаем средние по реализации композиции напряжения и деформации (матожидания дискретных случайных величин):
) дискретные значения напряжений и деформаций на k-й компоненте горного массива в представительном объеме. Домножая на γk и суммируя по k, получаем средние по реализации композиции напряжения и деформации (матожидания дискретных случайных величин):
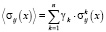 ,
,
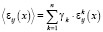 . (1)
. (1)
Таким образом, стационарность обеспечивается требованием воспроизведения концентраций на всех уровнях объема от представительного dV до общего V. Эргодичность обеспечивается равенством среднего по реализации (1) среднему по представительному объему:
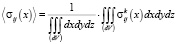 , (2)
, (2)
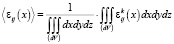 .
.
Основные формулы для k-й компоненты горной породы
Соотношения Коши для деформаций всех включений из k-ого однородного изотропного материала (компоненты) имеют вид [3, 6]:
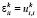 (
(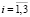 ), (3)
), (3)
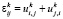 (
(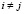 ,
, 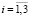 ,
, 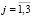 ),
),
где 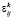 (
(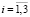 ,
, 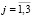 ) – компоненты деформаций по Коши,
) – компоненты деформаций по Коши, 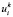 – проекции вектора перемещений для компоненты горной породы с номером k, при этом
– проекции вектора перемещений для компоненты горной породы с номером k, при этом 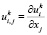 (
(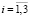 ,
, 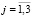 ).
).
Для изотропных тел соотношения обобщенного закона Гука известны из курса сопротивления материалов. В принятых выше обозначениях в развернутой форме связь между компонентами тензора напряжений и деформациями по Коши имеет вид [2, 3, 6]:
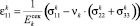 ,
,
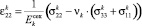 ,
,
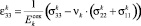 , (4)
, (4)
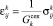 (
(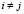 ,
, 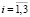 ,
, 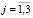 ),
),
где 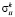 (
(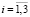 ) – нормальные напряжения,
) – нормальные напряжения, 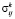 (
(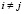 ,
, 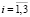 ,
, 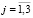 ) – касательные напряжения.
) – касательные напряжения.
Одними из основных уравнений механики твердого тела является система уравнений совместности, которая содержат шесть уравнений [3, 6]:
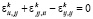 (
(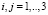 ,
, 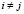 ), (5)
), (5)
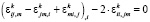 ,
,
(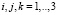 ,
, 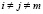 ).
).
Уравнения движения элементарного объема твердого тела с постоянной плотностью ρ можно записать в виде
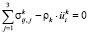 (i = 1,..,3), (6)
(i = 1,..,3), (6)
где 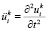 .
.
Эффективный обобщенный закон Гука для модели в среднем изотропной горной породы или почвы
На первом шаге используем гипотезу Фойгта о том, что при простейшем нагружении в макроточке горной породы имеет место однородная деформация [2, 3, 6], т.е. для любой компоненты параллелепипеда верны соотношения: 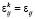 (
(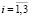 ,
, 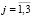 ). Запишем закон Гука (4) для k-й компоненты элементарного параллелепипеда в виде
). Запишем закон Гука (4) для k-й компоненты элементарного параллелепипеда в виде
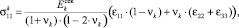
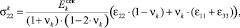 (7)
(7)
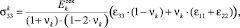
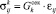 , (
, (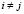 ,
, 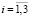 ,
, 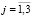 ).
).
Для нахождения эффективных характеристик по Фойгту определим средние значения напряжений 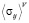 (
(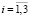 ,
, 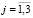 ), действующих на все компоненты горной породы, с помощью статистического усреднения дискретных случайных величин
), действующих на все компоненты горной породы, с помощью статистического усреднения дискретных случайных величин 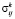 (
(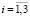 ,
, 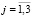 ) (7):
) (7):
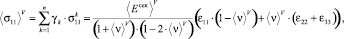
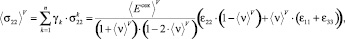 (8)
(8)
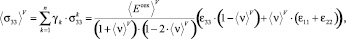
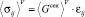 , (
, (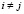 ,
, 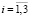 ,
, 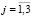 ).
).
где усредненные значения по Фойгту ⟨Eсек⟩Н и ⟨ν⟩V в (8) определяются выражениями
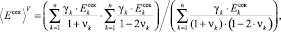 (9)
(9)
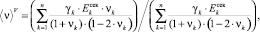 (10)
(10)
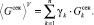 (11)
(11)
Далее применим гипотезу Рейсса о том, что при простейшем нагружении в представительном объеме горной породы или грунте имеет место однородное напряженное состояние [2, 3, 6], т.е. для любой компоненты выбранного параллелепипеда верны соотношения: 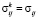 (
(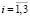 ,
, 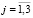 ). Подставляя их в (4), запишем закон Гука для k-й компоненты элементарного параллелепипеда:
). Подставляя их в (4), запишем закон Гука для k-й компоненты элементарного параллелепипеда:
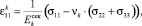
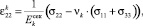
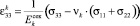 , (12)
, (12)
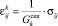 , (
, (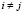 ,
, 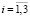 ,
, 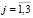 ).
).
Для нахождения эффективных характеристик по Рейссу определим средние значения деформаций ⟨εij⟩R (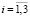 ,
, 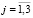 ) по всем компонентам горной породы в элементарном параллелепипеде с помощью статистического усреднения дискретных случайных величин
) по всем компонентам горной породы в элементарном параллелепипеде с помощью статистического усреднения дискретных случайных величин 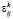 (
(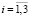 ,
, 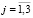 ) (12):
) (12):
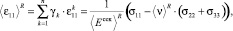
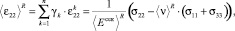 (13)
(13)
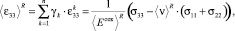
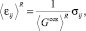 (
(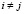 ,
, 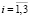 ,
, 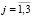 ),
),
где усредненные значения ⟨E⟩R и ⟨ν⟩R в (21)–(24) определяются выражениями
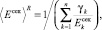 (14)
(14)
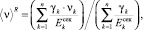 (15)
(15)
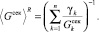 (16)
(16)
Как установлено в работах [2, 3, 6], эффективное приближение свойств композиционных материалов для практических целей может с достаточной точностью ограничиваться вычислением приближения Хилла модуля Юнга ⟨Eсек⟩Н, модуля сдвига ⟨Gсек⟩Н и коэффициента Пуассона ⟨ν⟩H, полученных как среднее арифметическое значение (9)–(11), а также (14)–(16):
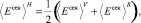
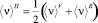 , (17)
, (17)
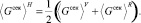
Эффективные уравнения неразрывности деформаций и движения элементарного объема в среднем изотропной упругой горной породы
Целью исследования данного раздела является обоснование того, что с помощью вычисленных эффективных значений можно решать геомеханические задачи.
Отметим также, что в силу линейности решаемой задачи для горной породы или грунта в рамках построенной модели любую динамическую задачу для весомого массива породы или почвы можно представить как простую суперпозицию решения динамической задачи для невесомой среды с механическими характеристиками породы и статической задачи для весомого слоя с теми же механическими характеристиками.
Поэтому в данном разделе рассматриваются уравнения динамики только для невесомого тела с механическими характеристиками породы.
Не повторяя известные результаты работы [3], посвященной механике композиционных тел, можно записать, что для представительного объема в среднем изотропной модели горной породы или грунта уравнения совместности деформаций для эффективных деформаций ⟨εij⟩ принимают вид
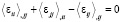
(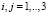 ,
, 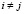 ), (18)
), (18)
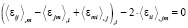 ,
,
(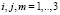 ,
, 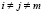 ).
).
Уравнения движения для эффективных напряжений ⟨σij⟩, вычисленных для представительного объема, приобретут вид [3]:
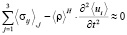 , (
, (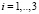 ), (19)
), (19)
где эффективную плотность породы или грунта по Хиллу ⟨ρ⟩H можно определить по формуле
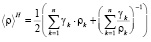 .
.
Эффективные уравнения динамики для горной породы или грунта
Уравнения (18) и (19) в совокупности с (17) позволяют методически просто повторить вывод уравнений динамики для породы или грунта с учетом дополнительного неопределенного параметра ⟨Gсек⟩Н (модуля сдвига) по аналогии с эффективными уравнениями композиционной среды [2, 3].
Опустим вывод эффективных уравнений в напряжениях Бельтрами – Митчелла и продемонстрируем влияние третьего свободного параметра ⟨Gсек⟩Н на уравнения Ламе.
Для вывода эффективных динамических уравнений Ламе теории упругости горной в среднем изотропной породы с тремя независимыми параметрами, ⟨Eсек⟩Н, ⟨Gсек⟩Н и ⟨ν⟩H в дальнейшем понадобятся обратные соотношения, когда напряжения выражены через деформации по Коши [3]:
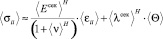 (
(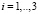 ), (20)
), (20)
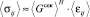 (
(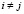 ,
, 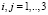 ),
),
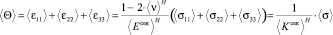 ,
,
где
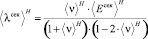 ,
, 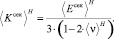
Используя эффективные уравнения равновесия (19), эффективные уравнения обобщенного закона Гука в форме (20), а также очевидную связь средних по представительному объему (в смысле операций (1) и (2)) деформаций и перемещений в виде
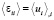 (
(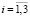 ),
), 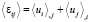 (
(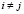 ,
, 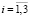 ,
, 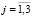 ),
),
можно получить эффективные уравнения Ламе, совершенно аналогично известной системе для однородного изотропного материала [3], которые можно записать с использованием оператора Лапласа в виде
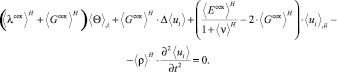 (21)
(21)
Эта система уравнений может быть получена из соответствующей системы уравнений Ламе для упругого ортотропного материала, в котором по всем трем направлениям положены одинаковые, но независимые 3 коэффициента упругости ⟨Eсек⟩Н, ⟨Gсек⟩Н и ⟨ν⟩H.
Совершенно аналогичный результат можно получить и для динамических уравнений Бельтрами – Митчелла, которые в данном случае также будут прямым следствием уравнений упругого ортотропного тела, решаемых всеми известными программами конечноэлементного анализа.
Определение скорости распространения волн в горных породах и почвах, имеющих в качестве независимых три параметра упругости
Отметим, что получение стандартного волнового уравнения, как это делалось в [3], невозможно. Однако можно использовать подход, изложенный в [9].
Предварительно продифференцируем каждое уравнение (21) по соответствующей координате xi и сложим результаты:
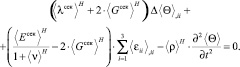 (22)
(22)
Применим метод разделения переменных для изучения волнового уравнения (22). Пусть 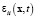 можно представить в виде
можно представить в виде
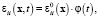 (23)
(23)
где
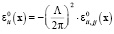 , (24)
, (24)
φ(t) – безразмерная функция времени, Λ – максимальная длина объемной волны.
Подставляя (23) и (24) в (22), получаем дифференциальное уравнение для φ(t) в виде
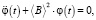
где ⟨B⟩ – эффективная циклическая частота колебаний породы или грунта, квадрат которой определяется уравнением
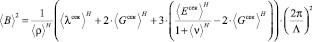 .
.
В этом случае эффективная скорость распространения объемной волны 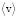 будет определяться уравнением
будет определяться уравнением
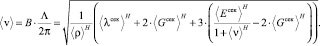
Учитывая, гипотезу о том, что 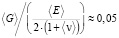 [4–6] можно получить, для геомеханических расчетов всего массива над выработкой следует использовать другую формулу определяющую эффективную скорость волны в горной породе ⟨v⟩гео с учетом специфического пластического состояния массива, соответствующего закону Мора-Кулона на некотором удалении от поверхности Земли и границы выработки:
[4–6] можно получить, для геомеханических расчетов всего массива над выработкой следует использовать другую формулу определяющую эффективную скорость волны в горной породе ⟨v⟩гео с учетом специфического пластического состояния массива, соответствующего закону Мора-Кулона на некотором удалении от поверхности Земли и границы выработки:
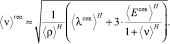
Необходимо отметить, что найденные приближения скоростей распространения объемной волны в горной породе основаны на линеаризованных уравнениях состояния и той гипотезе, что эффективный секущий модуль Юнга ⟨Eсек⟩Н и эффективный секущий модуль сдвига ⟨Gсек⟩Н, вычисленные по реализации линеаризованных законов деформирования компонент породы или почвы, совпадают с достаточной точностью с секущими линеаризующими модулями, полученным прямым испытанием представительного объема породы или почвы.
Заключение
Впервые предложен метод теоретической оценки линеаризованных механических свойств горных пород или почв для трех независимых параметров (модуля Юнга почвы, модуля сдвига, коэффициента Пуассона). Метод основан на линеаризации диаграммы деформирования каждой из компонент и на применении оценки Хилла упругих свойств горной породы или почвы, по аналогии с механикой композиционных, в среднем изотропных материалов.
В работе получены эффективные уравнения динамики горной породы в перемещениях на основе упругих уравнений состояния в среднем изотропной среды с тремя независимыми эффективными модулями, имеющими одинаковые значения во всех трех направлениях. Установлено, что структура уравнений полностью сохраняется такой же, как и в однородном случае для однородного тела с точностью до замены деформаций, напряжений и перемещений на средние по представительному объему горной породы или почвы величины. При этом в качестве усредненных упругих характеристик необходимо использовать полученные средние значения по Хиллу (17) модуля Юнга, модуля сдвига, коэффициента Пуассона и плотности (19).
Установлено, что теоретическое определение эффективной скорости распространения волны в горном массиве существенно зависит от всех трех параметров (эффективных модуля Юнга, модуля сдвига и коэффициента Пуассона). Ошибка определения эффективной скорости для изотропного материала (для двух независимых параметров упругости) в 1,5 раза превосходит ошибку гипотезы о вычисляемости модуля сдвига через модуль Юнга и коэффициент Пуассона и, например, на проволоке из чугунов может достигать 30 % [10].
Результаты данных исследований позволяют решать задачи геомеханики и строительства с помощью стандартного конечноэлементного обеспечения, например ANSYS.
Установлено, что при решении задач геомеханики, когда модуль Юнга, коэффициент Пуассона и модуль сдвига не связаны между собой известными соотношениями, в стандартных программах конечноэлементных расчетов следует пользоваться моделью ортотропного материала, однако следует задавать упругие характеристики в различных направлениях наборами из трех одних и тех же независимых значений (модуля Юнга, коэффициента Пуассона и модуля сдвига).
Исследования, изложенные в данной статье, позволяют определять эффективные свойства пород и почв по результатам подбора значений модуля Юнга горного массива на уже существующем объекте и использовать эти результаты в качестве прогноза при проектировании соседних аналогичных объектов, так как в этом случае при подборе значений инженер будет фактически выполнять теоретическое определение эффективных линеаризованных свойств горной среды по результатам наблюдений поведения объекта, находящегося в сходных условиях эксплуатации.
Библиографическая ссылка
Кравчук А.С., Смалюк А.Ф., Славашевич С.И., Мисников В.А. ТЕОРИЯ ОПРЕДЕЛЕНИЯ ЛИНЕАРИЗОВАННЫХ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ПОРОД И ГРУНТОВ ПО ИХ ОБЪЕМНОМУ СОСТАВУ // Успехи современного естествознания. 2018. № 12-2. С. 358-367;URL: https://natural-sciences.ru/ru/article/view?id=37021 (дата обращения: 22.01.2026).
DOI: https://doi.org/10.17513/use.37021



