Основной научной сферой применения данных глобальных навигационных спутниковых систем (ГНСС) продолжают оставаться геодинамические исследования, но их всё чаще применяют для решения задач сейсмологии, связанных с сильными землетрясениями. Данные ГНСС-измерений позволяют регистрировать и определять косейсмические (постоянные) смещения земной поверхности вследствие землетрясений, которые используются при моделировании (точнее, определении параметров модели) очага землетрясения [1, 2].
Чаще всего косейсмические смещения определяют по изменению среднесуточных координат геодезических пунктов, но они могут рассчитываться также и с использованием так называемой кинематической обработки, в результате которой получаются временные серии практически мгновенных координат с малым шагом дискретизации, обычно 1 с или даже менее [3, 4]. Кинематическая обработка ГНСС-измерений может проводиться с высокой точностью и практически в режиме реального времени. Например, при использовании метода Precise Point Positioning (PPP) [4, 5] ошибка определения мгновенного положения антенны находится на сантиметровом уровне. Вычисляемые таким способом косейсмические смещения земной поверхности дают возможность моделировать очаг землетрясения так же, как и при использовании среднесуточных координат ГНСС-антенны. При этом на получение решения после начала землетрясения требуется не больше нескольких минут [1].
Изучение очага землетрясения важно для понимания тектоники и реконструкции геодинамической обстановки в конкретном регионе. Основной же целью оперативного определения параметров модели очага землетрясения является уточнение опасности, которую несёт это землетрясение, в том числе оценка вероятности возникновения цунами. К настоящему времени созданы, тестируются и уже показывают первые результаты работы системы оперативного определения параметров очага землетрясения на основе ГНСС-измерений в Калифорнии [6] и в Японии [7].
Системы раннего предупреждения о цунами (СРПЦ) являются основной и наиболее перспективной сферой применения ГНСС-координат, получаемых в реальном времени [7, 8]. ГНСС-измерения в СРПЦ могут решить проблемы прогноза цунами для побережий, близких к эпицентру землетрясения. Это не только проблема недооценки опасности цунами после сильнейших землетрясений с магнитудой 8,5 и более, но и проблема ложных тревог цунами, подавляющее большинство которых приходится на землетрясения с магнитудой 7–8. Для расширения сферы применения ГНСС-измерений в СРПЦ на эти землетрясения необходимо уметь определять косейсмические смещения быстро и максимально точно.
Вопросы о точности оперативного определения смещений по ГНСС-измерениям остаются малоизученными. Одни из немногих оценок можно найти в работах [1, 9, 10], но они либо приводятся без обоснования, либо получены обработкой методами, неприменимыми в реальных условиях. В настоящей работе проведено сравнение различных методов и определена достижимая точность оперативного определения косейсмических смещений по ГНСС-измерениям.
Материалы и методы исследования
Косейсмическое смещение вычисляется как разность между оценками положения ГНСС-антенны до и после смещения. Если обе эти оценки вычисляют по измерениям, то в общем случае положение ГНСС-антенны можно представить как значение функции, аппроксимирующей соответствующий ряд координат, во время смещения. На практике сложные аппроксимирующие функции практически не используются, наиболее часто положение ГНСС-антенны определяется усреднением ряда координат.
Для моделирования ошибок определения смещений в настоящей работе использован статистический подход. Он, в отличие от аналитического подхода [9], заключается в получении и статистическом анализе выборки ошибок определения смещений (ООС).
Для формирования выборки ООС использованы ряды координат, полученные обработкой в режиме реального времени данных ГНСС-измерений, и не содержащие реальных смещений. Если по таким данным некоторым способом определить смещение, то оно будет численно равно ООС, поскольку в действительности антенна была неподвижна. Этот подход правомерен, так как точность определения координат не зависит от наличия и величины реального смещения, по крайней мере в используемых программах для обработки ГНСС-измерений.
В качестве исходных данных были использованы наблюдения с шагом дискретизации 1 с и суммарной продолжительностью около 2400 суток, полученные на 150 станциях (рис. 1): 148 станциях ГНСС-сетей IGS и CORS, а также на двух станциях, расположенных в Хабаровском крае и обслуживаемых Институтом тектоники и геофизики ДВО РАН. Данные обрабатывались при полной имитации режима реального времени методом PPP, с использованием высокоточных поправок часов и орбит спутников, генерируемых и доступных также в режиме реального времени. Примерно три четверти данных были обработаны ранее в программе BKG Ntrip Client (BNC) и использована в работе [11] для моделирования шума в рядах ГНСС-координат. Остальные измерения относятся к ноябрю 2018 г. и обрабатывались в программе PPP Wizard (http://www.ppp-wizard.net/). Так же, как и в работе [11], к рядам координат применялась сидерическая фильтрация, если это было целесо- образно. Обе программы дали сопоставимые по точности ряды координат.
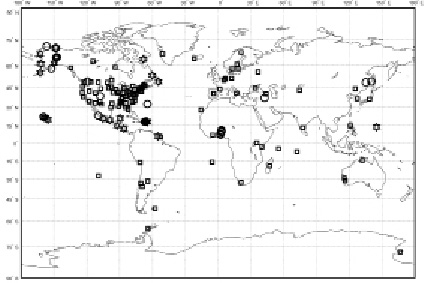
Рис. 1. Использованные в работе ГНСС-станции с данными: квадраты – 2016 г., кружки – 2018 г., звёзды – за оба периода
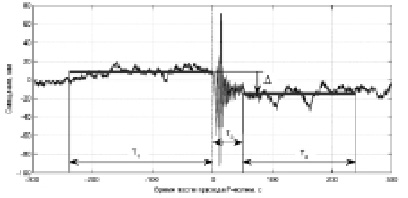
Рис. 2. Схема определения величины смещения усреднением мгновенных значений высокочастотных координат: T1, T3 – длины участков записи до и после смещения; T2 – длина исключаемого участка записи; Δ – смещение
Используемая схема определения смещений (рис. 2) включает три параметра, влияющих на точность и определяющих величину задержки получения результата. Параметр T1 определяет длину участка записи до начала смещения. Он не влияет на задержку получения результата и может быть сколь угодно большим. Параметр T2 определяет длительность исключаемой записи, не используемой для определения смещения. Она может содержать физическую реализацию смещения и сейсмические волны больших амплитуд. Её продолжительность может быть определена исходя из предварительно полученных оценок магнитуды и эпицентрального расстояния. Параметр T3 определяет длину участка записи после смещения. Задержка получения решения, таким образом, складывается из параметров T1 и T2.
В настоящей работе были использованы следующие методы определения статических смещений:
1. Усреднение рядов координат.
2. Аппроксимация рядов координат полиномами первой и второй степени.
3. Усреднение рядов координат до и после смещения с добавлением весовых коэффициентов, которые рассчитывались как
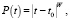
где t0 – время в середине вырезаемого фрагмента; W – коэффициент (оптимальное значение определено далее W = –2,5). Соответственно, положение до или после смещения определялось по формуле весового среднего:
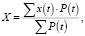
где x(t) – исходный ряд координат. Следует заметить, что дополнительные весовые коэффициенты для определения статических смещений в известных работах не используются.
Дополнительно к ООС по каждой из компонент (запад-восток, север-юг и вертикальной), определялись ошибки определения полных горизонтальных смещений:
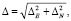
где 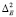 и
и 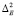 – ООС по компонентам запад-восток и север-юг, соответственно. Основная причина их использования – сильная зависимость соотношения точности определения координат по компонентам запад-восток и север-юг от широты [12], что подтверждается также и данными, полученными нами в работе [11].
– ООС по компонентам запад-восток и север-юг, соответственно. Основная причина их использования – сильная зависимость соотношения точности определения координат по компонентам запад-восток и север-юг от широты [12], что подтверждается также и данными, полученными нами в работе [11].
Результаты исследования и их обсуждение
Каждая полученная по всему массиву исходных данных выборка ООС содержала около 1,7 млн значений. В первую очередь было проведено сравнение точности определения смещений вышеперечисленными методами. Для этого для шести пар значений параметров T2 и T3 каждым методом были получены выборки ООС и рассчитаны среднеквадратические ошибки (СКО) определения полных горизонтальных смещений (таблица). Во всех случаях здесь и далее использовалось значение параметра T1 = 300 с.
Сравнение методов определения смещений
|
Метод |
СКО определения горизонтальных смещений, мм |
||||||
|
T2 = 30 с |
T2 = 60 с |
||||||
|
T3 = 30 с |
T3 = 90 с |
T3 = 270 с |
T3 = 30 с |
T3 = 90 с |
T3 = 270 с |
||
|
Усреднение |
8,0 |
8,0 |
8,4 |
8,6 |
8,5 |
8,9 |
|
|
Аппроксимация полиномами |
1-й степени |
9,6 |
8,6 |
8,7 |
12,8 |
10,5 |
10,0 |
|
2-й степени |
17,7 |
10,7 |
9,6 |
36,9 |
16,3 |
12,6 |
|
|
Усреднение с весовыми коэффициентами |
W = –1 |
6,6 |
6,5 |
6,6 |
7,7 |
7,5 |
7,6 |
|
W = –1,5 |
6,1 |
6,0 |
6,0 |
7,3 |
7,2 |
7,1 |
|
|
W = –2 |
5,9 |
5,8 |
5,8 |
7,2 |
7,0 |
6,9 |
|
|
W = –2,5 |
5,8 |
5,8 |
5,7 |
7,1 |
7,0 |
6,9 |
|
|
W = –3 |
5,8 |
5,8 |
5,7 |
7,1 |
7,0 |
6,9 |
|
Приведённые в таблице результаты показывают, что наименее точный способ определения смещений – аппроксимация полиномами. Метод усреднения точнее, и при его использовании не так сильно влияние параметров T2 и T3. Но наибольшую точность показал предложенный метод усреднения с использованием весовых коэффициентов: при значении W = –2,5 он даёт ошибки ещё на 17–32 % меньше. Таким образом, в качестве оптимального для дальнейших расчётов был принят метод усреднения рядов координат до и после смещения с весовыми коэффициентами. Пример статистического распределения ООС в одной из выборок (при значениях T2 = T3 = 30 с) показан на рис. 3.
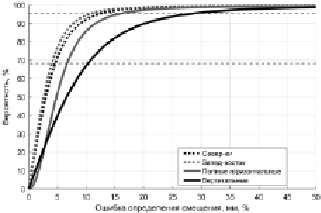
Рис. 3. Пример статистических распределений ошибок определения смещений. Горизонтальными линиями отмечены вероятности 68,27 % и 95,45 %
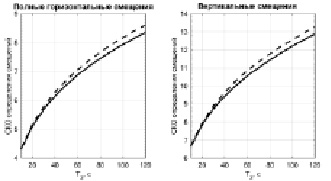
Рис. 4. Зависимости СКО определения смещений от параметра T2: сплошные линии – при задержке 5 минут, пунктир – при минимальной задержке (T2 + 30 с)
При выбранном методе определения смещений влияние параметров T1 и T3 на точность мало, в пределах 5 %. Наибольшее влияние на ООС оказывает значение параметра T2, то есть длина вырезаемого фрагмента. Зависимости СКО определения смещений от параметра T2 приведены на рис. 4. Из них следует, что потеря точности определения смещений от минимизации задержки невелика, особенно по сравнению с потенциальной потерей точности из-за завышения неправильно выбранного параметра T2. Поэтому, с одной стороны, рационально сократить время задержки получения результата ценой увеличения ошибки в среднем на несколько процентов. С другой стороны, важно правильно подбирать длину вырезаемого фрагмента, не допуская ни её чрезмерного завышения (что значительно повышает ООС), ни тем более занижения (тогда результат будут искажать сейсмические колебания).
Точность определения смещений на разных станциях отличается достаточно сильно, до четырёх раз, хотя, например, СКО на 75 % станций при T2 = 60 с, T3 = 30 с попадает в диапазон 4–7,5 мм. Для станций, расположенных в Хабаровском крае, при тех же параметрах были получены следующие оценки СКО: GEO0 (Хабаровск) – 6,2 мм, VANI (п. Ванино) – 12,2 мм. При этом видимой закономерности между точностью и местоположением станции не выявлено, кроме уже упомянутого влияния широты на соотношение точности по компонентам запад-восток и север-юг.
Выводы
В работе получены следующие основные результаты:
1. Предложен метод усреднения рядов координат до и после смещения с весовыми коэффициентами, который оказался на 17–32 % точнее наиболее часто используемого простого усреднения. Точность методов, использующих аппроксимацию рядов координат полиномами, значительно ниже, чем метода усреднения.
2. По результатам статистического анализа получены оценки точности оперативного определения статических смещений по ГНСС-данным. В среднем по всему набору исходных ГНСС-данных, полученных на 150 станциях, среднеквадратическая ошибка определения горизонтальных смещений находится в пределах 5–8 мм (вертикальных – 7–13 мм) и зависит в основном от продолжительности прохождения сейсмических волн больших амплитуд.
3. Точность определения смещений на разных станциях варьирует в широких пределах, но достаточно стабильна во времени и может быть оценена заранее. Такая оценка для двух станций, расположенных в Хабаровском крае (г. Хабаровск, п. Ванино), дала значения СКО горизонтальных смещений 6,2 и 12,2 мм соответственно (при T2 = 60 с, T3 = 30 с).
Полученные оценки точности оперативного определения статических смещений могут использоваться как в виде СКО, так и в виде статистических распределений при проектировании подсистем раннего предупреждения о цунами, использующих ГНСС-данные, и определении возможностей таких систем. При этом нецелесообразным видится расчёт и использование региональных статистических распределений. Для конкретных существующих ГНСС-станций рациональнее рассчитывать индивидуальные статистические распределения ООС, для проектируемых или гипотетических станций – средние общемировые, по возможности с коррекцией на ожидаемые соотношения точности по компонентам запад-восток и север-юг, в зависимости от широты.
Исследования выполнены в рамках государственного задания Института тектоники и геофизики им. Ю.А. Косыгина ДВО РАН и при финансовой поддержке РФФИ в рамках научного проекта № 18-35-00178.
Библиографическая ссылка
Пупатенко В.В. ТОЧНОСТЬ ОПЕРАТИВНОГО ОПРЕДЕЛЕНИЯ ПО ГНСС-ДАННЫМ СТАТИЧЕСКИХ СМЕЩЕНИЙ, ВЫЗВАННЫХ ЗЕМЛЕТРЯСЕНИЯМИ // Успехи современного естествознания. 2019. № 3-1. С. 78-83;URL: https://natural-sciences.ru/ru/article/view?id=37074 (дата обращения: 26.02.2026).
DOI: https://doi.org/10.17513/use.37074



