Высокая сельскохозяйственная нагрузка на районы земледельческой части Краснодарского края требует сохранения и воспроизводства плодородия этих почв.
Восстановление и развитие орошения и осушения земель намечено осуществить в два этапа: I – 2009–2015 гг., II – 2016–2020 гг. [1–3].
На первом этапе необходимо обеспечить восстановление, реконструкцию и эффективное использование имеющихся оросительных и осушительных систем, осуществить научные исследования и научно-технические разработки инновационного развития орошения и осушения земель. К 2015 г. намечено провести реконструкцию, модернизацию и повысить эффективность использования орошаемых земель на площади 2,2 млн га, осушаемых – 1 млн га. Ввод новых орошаемых и осушаемых земель намечен на 2014–2015 годы по 200 тыс. га в год.
На втором этапе намечено довести площади орошаемых и осушенных земель до уровня, позволяющего производить сельскохозяйственную продукцию в количестве, достаточном для удовлетворения потребности страны в продуктах питания.
Цена принимаемых решений очень велика. Необходимо определить оптимальный перечень мелиоративных работ, обеспечивающий максимальную эффективность мелиорации при заданных ограничениях на капиталовложения и другие ресурсы.
В последние годы из-за недостатка средств на мелиоративные мероприятия углубились явления вторичного засоления и осолонцевания почв в результате вымывания из пахотного слоя гумуса, кальция, коллоидных и питательных веществ. Из-за повышенных требований на подаваемую воду (не отвечающих истинным потребностям) образуются большие переполивы, приводящие к подъему уровня грунтовых вод и непроизводственному сбросу неиспользованной воды за пределы оросительной системы. В этой связи требуется обоснование приемов регулирования процессов на мелиорируемых землях [1].
В современном сельскохозяйственном производстве особенно важна проблема устойчивости агроландшафта. Для достижения оптимального уровня экологического равновесия и устойчивости агроландшафта необходим количественный подход. При этом экологические требования должны быть приоритетными.
Оптимизация распределения ресурсов при планировании мелиоративных мероприятий – сложная квалиметрическая задача. Постановка задачи при распределении ресурсов состоит в производстве сельскохозяйственной продукции в заданном объеме при сохранении экологической устойчивости агроландшафта. В каждом мелиоративном проекте проводится анализ влияния намечаемых мероприятий на окружающую среду, определяются меры по нейтрализации или ограничению ущерба.
Особенность оценки эффективности природоохранных проектов состоит в необходимости учета вероятностного характера происходящих процессов [4; 5]. Степень возможности определенных сценариев характеризуется их вероятностью или вероятностными распределениями. Для учета стохастического характера процессов необходим выбор подходящих вероятностных моделей.
Отличие проектов, разрабатываемых для детерминированных ситуаций, от проектов, учитывающих факторы неопределенности, состоит в том, что во втором случае условия реализации проекта неизвестны [6; 7].
Однако какова цена намечаемого мероприятия в совокупности обязательных к рассмотрению факторов и есть ли возможность оценки влияния каждого или их групп на конечный результат? Естественно, такая широта постановки вопроса не может быть решена экспериментально или только анализом и обобщением априорной информации. Именно для выхода из подобных ситуаций наиболее приемлемо математическое моделирование процессов, возможностями которого далее и воспользуемся. Была поставлена цель – разработать математическую модель процесса снижения цены намечаемых мелиоративных мероприятий [8; 9].
Материалы и методы исследования
В основе разрабатываемой математической модели заложены принципы количественных и качественных методов оценок природно-климатических, почвенных, водных и эколого-агроландшафтных критериев и показателей для принятия оптимальных решений на основе аппроксимации имеющихся данных.
Математические модели такого типа не могут быть конечного вида и находятся в состоянии совершенствования (дополнения) на протяжении всего своего времени использования. Путем добавления в них новых данных по рассматриваемым природно-климатическим, почвенным, водным и эколого-агроландшафтным показателям и критериям, а также степени их взаимовлияния друг на друга при различных условиях их сочетания программа коррелирует принимаемые решения для принятия оптимально адекватного управленческого решения для конкретного хозяйства [10; 11].
Составим математическую модель изменения цены мероприятий, обеспечивающих удовлетворительное мелиоративное состояние системы, максимальную прибыль с учетом потерь от неблагоприятного состояния.
Пусть цена намечаемого мероприятия – S и цена выполняемых мероприятий S(t) – непрерывная функция времени t. При t = 0 S(0) = S0 и функция S(t) – монотонно убывающая. Обозначим R – вероятность наступления неблагоприятного состояния. Заметим, что эта вероятность R(S) зависит от цены выполненных мероприятий. Намечаемые мероприятия образуют пуассоновский поток интенсивности l. В работе [1] получены основные характеристики случайных величин – цены состояния и промежутка времени до наступления благоприятного состояния.
Плотность вероятностей промежутка времени до наступления благоприятного состояния определяется следующим выражением:
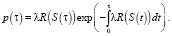
Обозначим Sm – минимальную цену мелиоративных мероприятий, при которых неудовлетворительное состояние системы наступает непременно.
Пусть K(τ) – ущерб, который будет нанесен мелиоративной системе, если удовлетворительное состояние системы наступит в момент времени τ.
Составим выражение для дохода Q:
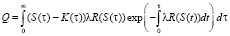(1)
и потребуем, чтобы выполнялось условие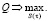 
Используя методы вариационного исчисления, заменим S(τ) на S(τ) + δS(τ). При этом Q изменится на величину
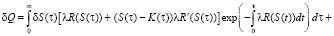
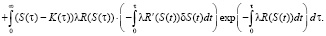
После преобразования получим:
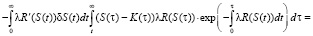
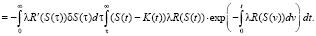(2)
При δS(τ) под знаком интеграла в δQ стоит выражение
–
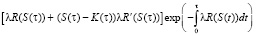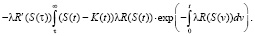(3)
На экстремали [1] оно должно равняться нулю:
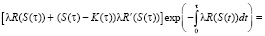
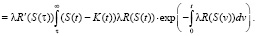(4)
Разделим обе части этого выражения на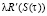 
и продифференцируем по t. Тогда получим:
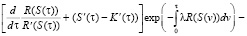
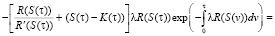
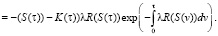
Сократим экспоненты и приведем подобные
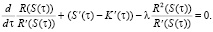
Вычислив производную
,
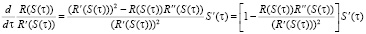разделим обе части этого выражения на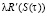 
и продифференцируем по t. После преобразований получим дифференциальное уравнение для оптимального значения S(τ):
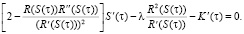(5)
Дифференциальное уравнение (5) – первого порядка относительно S(τ).
Чтобы найти произвольную постоянную, входящую в общее решение уравнения (5), составим дополнительное условие, положив на экстремали τ = 0. Получим:
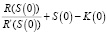
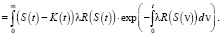(6)
Далее рассмотрим частный случай выражения ущерба K(τ) = K0τ. Дифференциальное уравнение для линейной зависимости K(τ) будет иметь вид:
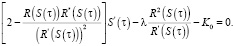(7)
Можно показать, что решение уравнения (7) имеет вид S(τ) = S0.
Тогда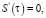 
и в результате получаем алгебраическое уравнение:
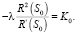(8)
Примем зависимость цены от времени функцией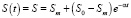 
. В этом случае S(0) = S0 и 
.
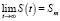Исходя из полученного, выражение (8) принимает вид:
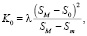(9)
где Sm – минимальная цена мелиоративных мероприятий, при которых неудовлетворительное состояние системы наступает непременно, R(Sm) = 1;
SM – максимальная цена мероприятий, при которой не отмечается ущерб природной среде, R(SM) = 0 [12; 13].
Оптимальную стоимость мелиоративных мероприятий получаем из выражения (9):
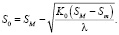(10)
Полученная нами формула (10) позволяет количественно оценить ущерб с учетом вероятностной неопределенности экологических, экономических и других факторов проекта, произвести выбор оптимальных параметров эксплуатации мелиоративной системы, а также решать другие задачи, связанные с рациональным использованием природных ресурсов.
Одним из приоритетных направлений мелиоративных проектов является разработка и внедрение природоохранных технологий, которые обеспечивают повышение экологической безопасности агроландшафтов и способствуют предотвращению негативных процессов при антропогенном воздействии. Примеры возможных мероприятий: система обработки почвы, направленная на улучшение ее структуры, строения и водно-физических свойств; внесение органических и минеральных удобрений; мероприятия по устранению щелочности и кислотности почв, осушению заболоченных земель; промывка почв. Затраты на промывку почвы зависят от степени засоления, следует также учитывать ущерб от недопромывки почв [14; 15].
Результаты исследования и их обсуждение
Мелиоративные объекты должны быть объектами повышенного внимания и ответственности, что в свою очередь накладывает особые требования к методам оценки влияния проектируемых и эксплуатируемых мелиоративных систем.
Исследования должны основываться на «комплексном подходе» с определением степени влияния каждого мероприятия на планируемый результат и учетом как можно большего количества взаимовлияющих факторов на результат других выполняемых мероприятий, входящих в состав «комплексного подхода». Однако из-за различных материально-технических возможностей и экономических ресурсов хозяйств не все и не в полном объеме фундаментальные положения могут быть реализованы, что затрудняет создание единой межхозяйственной (межрегиональной) базы данных с достаточной степенью адекватности.
В связи с этим одним из основных направлений наших исследований является разработка математической модели для принятия управленческих решений по рациональному возделыванию сельскохозяйственных культур. Полученные результаты могут усовершенствовать теоретические основы формирования оценки мелиоративного состояния агроландшафтов с учетом неопределенности исходных данных.
В основе разрабатываемой математической модели заложены принципы количественных и качественных методов оценок природно-климатических, почвенных, водных критериев и показателей для принятия оптимальных эколого-адаптивных решений на основе аппроксимации имеющихся данных. Характеристики климатических ресурсов: количество солнечной радиации, сумма активных температур, максимальные, минимальные и среднегодовые значения температуры воздуха, количество осадков за вегетационный период, по месяцам года и др. Почвенные ресурсы характеризуются типом и разновидностью почвы, мощностью гумусового слоя, рН почвы, содержанием питательных элементов, физическим состоянием (структурно-агрегатный состав, влагоемкость, плотность, водопроницаемость).
Антропогенное воздействие на агроландшафт характеризуют внесенные удобрения (органические и минеральные), пестициды (вид, количество), семена, мелиоранты, используемая техника и тому подобное.
Разрабатываемый подход может быть научно обоснованной стратегией природопользования, совершенством технологий мелиорации, так как позволяет учесть антропогенное воздействие и количественные оценки природно-климатических, почвенных и водных ресурсов. Использование результатов приостановит прогрессирующее загрязнение окружающей среды и деградации природных экосистем.
Заключение
Экологические проблемы должны быть учтены на всех уровнях планирования. Необходимо создать оптимальную систему природопользования и землепользования, сочетающую экономическую эффективность и экологическую устойчивость. При выборе управляющего воздействия часто возникает вопрос о замене одних управляющих факторов другими, имеющими сходное влияние на перевод объекта управления в данное состояние. Намеченный подход позволяет решить эту задачу и найти оптимальное соотношение мероприятий по предотвращению экологического ущерба. Предложенная модель дает возможность изменять входные условия, имитировать реальный режим эксплуатации, исследовать отклики объекта на изменение начальных условий, на изменение параметров моделируемой системы. В ходе разработки проектов сопоставляется несколько вариантов.
Разработанная модель может быть использована для сравнительного анализа различных вариантов природоохранных мероприятий, для определения очередности осуществления мероприятий, своевременной разработки мероприятий по недопустимому ухудшению почвенно-мелиоративного состояния орошаемых земель.
Библиографическая ссылка
Сафронова Т.И., Приходько И.А. ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ АГРОЛАНДШАФТОВ // Успехи современного естествознания. – 2019. – № 3-2. – С. 204-209;URL: https://natural-sciences.ru/ru/article/view?id=37094 (дата обращения: 20.04.2024).