Актуальность работы связана с необходимостью выявления закономерностей естественного формирования пойменных насаждений Западно-Казахстанской части бассейна реки Урал. До настоящего времени для этих лесов разработаны нормативно-справочные материалы, относящиеся только к стандартным и сортиментным таблицам, что крайне недостаточно для полной оценки ресурсно-экологического потенциала лесов региона. Следует признать, что «Нормативы для таксации лесов Казахстана», изданные в 1987 г., требуют модернизации информационного наполнения. Так, в них отсутствует системный комплекс решений по строению и продуктивности древостоев, учитывающий всё многообразие экологических условий произрастания насаждений разного породного состава, полноты и густоты.
Существенное увеличение числа показателей, составляющих содержание таксационных таблиц, объёма цифровой информации, характеризующего состояние древесных ресурсов, привело к необходимости разработки и внедрению в производство информационно-справочных систем лесотаксационных нормативов. Актуальность темы напрямую связана с проблемой внедрения цифровой экономики в лесную отрасль.
Цель исследования: выявление закономерностей статистических моделей строения древостоев разного породного состава, полноты и густоты по группам типов лесов на примере роста и развития тополя черного в осокорниках поймы р. Урал в границах Западно-Казахстанской области. Представленной работой показаны возможные диапазоны изменения масштаба и формы кривых распределения деревьев по толщине для многомерной классификации вариационных рядов и построения нормативов роста, строения и продуктивности древостоев.
Материалы и методы исследования
Оценка качественного состояния лесов базируется на знании закономерностей роста и строения древостоев, которые определяют динамику их продуктивности. Под закономерностями строения древостоев понимается распределение числа деревьев, суммы площадей сечения, запаса, категорий крупности, дровяной древесины, фракционного состава фитомассы в размахе варьирования размера деревьев и, прежде всего, по толщине. Изучение динамики формирования структуры этих показателей в древостоях разной начальной густоты по типам лесорастительных условий имеет исключительно важное значение для выбора наиболее продуктивных, с лучшими товарными характеристиками древостоев. А это в свою очередь позволяет скорректировать и оптимизировать режим промежуточного и главного лесопользования, построить модели прогнозирования производительности лесов. Наряду с этим знание закономерностей динамики строения древостоев является теоретической основой разработки методов таксации и учёта лесного и лесосечного фонда, формирования товарно-денежного потенциала лесов.
Общеизвестна теория строения древостоев, базирующаяся на параметрических и непараметрических методах анализа вариационных рядов.
Параметрические методы строения древостоев
Широкое применение в лесной таксации при сглаживании отдельных рядов распределений числа деревьев по толщине получили модели двух параметрических кривых Гаусса (кривая нормального распределения) и четырёх параметрических кривых К. Пирсона (тип I) и Шарлье (тип А). Статистическими параметрами для построения теоретических кривых являются: средняя арифметическая величина (Ẍ), стандартное отклонение (σ), асимметрия (As) и эксцесс (E).
Стандартное отклонение – это число, описывающее, насколько значения данных отличаются от среднего. Понятие стандартного отклонения является очень важным в статистике, поскольку оно представляет собой основной инструмент определения степени случайности отклонений отдельных значений от их среднего.
Асимметрия – скошенность ряда распределения возникает вследствие того, что какие-либо факторы действуют в одном направлении сильнее, чем в другом, или процесс развития явления таков, что доминирует какая-то причина. Кроме того, природа некоторых явлений такова, что имеет место асимметричное распределение
Эксцесс – крутизна ряда распределения, статистика, характеризующая степень остроты пика распределения случайной величины.
Указанные параметры определяются для каждого ряда использованием программы описательной статистики в среде MS Excel. Полученные значения параметров включаются в расчёт теоретических кривых распределения с последующим сравнением с эмпирическими рядами. Критериальная оценка соответствия теоретических распределений эмпирическому ряду осуществляется по критерию χ-квадрат Пирсона. Существующие методы строения древостоев подробно изложены в работе А.А. Макаренко [1]. По его рекомендации следует использовать метод построения рядов с постоянным числом классов, равным 10. Такое число отвечает требованиям математической статистики, обеспечивает нахождение достоверных параметров или статистик рядов распределения при минимально возможном числе наблюдений. Критически оценивая параметрические методы строения древостоев, следует указать на наличие средних, слабых и недостоверных взаимосвязей между параметрами масштаба и формы рядов распределения, что ставит под сомнение результаты моделирования триады: ход роста – строение – продуктивность.
Непараметрические методы строения древостоев
Методы основаны на построении вариационных рядов накопленного распределения частот и анализа изменений квантилей ряда. Широкое применение в исследованиях строения древостоев нашла модель аппроксимации эмпирических распределений Н.Л. Джонсона. Также нами использована модель В.К. Хлюстова с алгоритмом расчёта теоретических частот [2]. Для аппроксимации эмпирических распределений по указанными моделями на кафедре лесоводства РГАУ-МСХА имени К.А. Тимирязева была разработана программа «Лескаф».
Новое научно-методическое решение задачи динамики строения древостоев было найдено и предложено к внедрению более 10 лет тому назад [3]. Основным элементом этого метода моделирования возрастного распределения частот вариационного ряда является доказательство того, что любой размах варьирования ряда распределения делится на две равные части. Так, при 10 классовых промежутках середина ряда соответствует пятому классу, при 12 – шестому, при 14 – седьмому и т.д. Затем накопленная частота распределения, названная в теории таксации рангом деревьев, выражается в долях частоты, соответствующей середине ряда.
Экспериментальный материал и объём выполненных работ
Полевой таксационный материал был собран в осокорниках Западно-Казахстанской части поймы р. Урал. При этом полученные данные охватывают все лесорастительные условия тополя чёрного (табл. 1).
Результаты исследования и их обсуждение
Масштаб ряда, или иными словами, размах варьирования является основным показателем, определяющим форму рядов распределения. Еще на ранних этапах исследований строения древостоев В. Вейзе [4] и А.В. Тюриным [5] отмечено, что максимальная толщина деревьев в спелых древостоях составляет от 1,5 до 1,6 от среднего диаметра, а минимальная 0,3 и не зависит от полноты, бонитета и, в значительной степени, от возраста древостоев. Согласно этому положению наиболее чётко размах варьирования толщины деревьев связан со средним диаметром [6, 7]. Наглядно эта закономерность для тополя чёрного в осокорниках представлена на рис. 1.
Судя по графику, предельные границы толщины деревьев имеют некоторый разброс. Этот разброс становится шире по мере увеличения среднего диаметра древостоя. Интерпретируя указанную закономерность, представим вначале линии регрессии, соответствующие средним значениям минимальных диаметров и средним значениям максимальных диаметров. При этом уравнения регрессии имеют следующий вид:
d min регр = 0,1089*D 1,3931 , (1)
d max регр = 6,5804*D 0,5939 . (2)
Вместе с тем при оценке размаха варьирования следует учитывать возможные их варианты с учётом возможного отклонения от средней линии регрессии, которые с возрастом древостоя при его естественном формировании существенно не изменятся. Так, возможные варианты размаха варьирования могут иметь комбинации, представленные в табл. 2.
Таблица 1
Объекты для проведения статистического анализа
|
Группа типов леса |
Количество пробных площадей, ед. |
Количество измерений деревьев, ед. |
|
|
диаметров |
высот |
||
|
Осокорники низинные прирусловые (Онпр) |
17 |
4185 |
353 |
|
Осокорники низинные центральной поймы (Онц) |
8 |
1809 |
53 |
|
Осокорники средних уровней прирусловой поймы (Оспр) |
47 |
11109 |
648 |
|
Осокорники средних уровней центральной поймы (Осц) |
48 |
10128 |
228 |
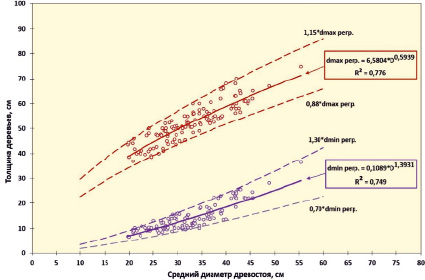
Рис. 1. Линии регрессии размаха варьирования толщины деревьев в древостоях тополя чёрного (условные обозначения см. в тексте)
Таблица 2
Возможные варианты размаха варьирования рядов распределения числа деревьев по толщине
|
№ п/п |
Левая граница |
Правая граница |
|
1 |
1,15*dmax регр = f(D) |
0,7*dmin регр = f(D) |
|
2 |
1,15*dmax регр = f(D) |
dmin регр = f(D) |
|
3 |
1,15*dmax регр = f(D) |
1,3*dmin регр = f(D) |
|
4 |
dmax регр = 6,5804*D0,5939 |
0,7*dmin регр = f(D) |
|
5 |
dmin регр = 0,1089*D1,3931 |
|
|
6 |
1,3*dmin регр = f(D) |
|
|
7 |
0,88*dmax регр = f(D) |
0,7*dmin регр = f(D) |
|
8 |
0,88*dmax регр = f(D) |
dmin регр = f(D) |
|
9 |
0,88*dmax регр = f(D) |
1,3*dmin регр = f(D) |
Таким образом, точное определение размаха варьирования является важнейшим звеном классификации рядов распределения.
Многообразие формы кривых распределения деревьев по толщине требует систематизации (классификации) рядов с учётом размаха варьирования диаметров [8–11]. Для решения этой задачи использованы непараметрические методы строения древостоев.
Наряду с регрессиями масштаба рядов распределения приводится графическая интерпретация предельных и среднестатистических кривых распределения частот, что позволяет судить о широком диапазоне возможных вариантов встречаемости рядов распределения. На рис. 2 явно просматриваются ряды, как с левосторонней, так и с правосторонней асимметрией.
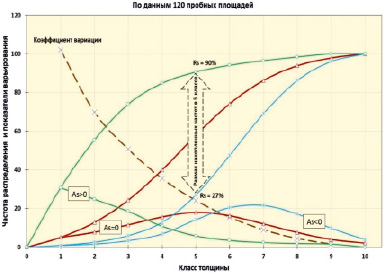
Рис. 2. Предельно асимметричные и среднестатистическое распределения частоты встречаемости деревьев по толщине (условные обозначения см. в тексте)
В соответствии с методикой моделирования строения древостоев, накопленное распределение частот в ряду с предельной правосторонней асимметрией (As > 0) ранг деревьев в центральном (пятом) классе насчитывает 90 %. В ряду с предельной левосторонней асимметрией (As < 0) ранг деревьев в центральном (пятом) классе составляет 27 %. Среднее распределение числа деревьев по всей совокупности вариационных рядов близко по форме к кривой нормального распределения, с максимумом частот в центральном классе.
Следует отметить закономерное уменьшение коэффициента вариации накопленной частоты по классам толщины от значительной (100 %) в первом классе, до незначительной (3 %) в девятом классе. Такая высокая изменчивость накопленной частоты характерна для насаждений тополя чёрного осокорниковой формации, которая в пойменных лесах р. Урал постоянно подвергается экстремальному воздействию факторов, связанных с подтоплением корневых систем деревьев [12–14].
Указанные особенности формирования насаждений тополя чёрного следует учитывать при проведении многомерной классификации рядов распределения и моделирования возрастного изменения строения древостоев.
Выводы
Среднестатистические параметры масштаба рядов распределения по максимальному и минимальному диаметру деревьев имеют взаимосвязь со средним диаметром с показателями детерминации R2max = 0,776, R2min = 0,749. Предельные отклонения минимальных и максимальных диаметров от среднестатистических значений, полученных по модели, находятся в диапазонах: 0,70*dmin.регр.÷1,30*dmin.регр. и 0,88*dmax.регр. ÷1,15*dmax.регр.
Форме рядов распределения древостоев присуща как левосторонняя, так и правосторонняя асимметрия. Предельные значения ранга деревьев в пятом классе варьируют от 27 до 90 %. Среднестатистическая форма распределения соответствует кривой, близкой к кривой нормального распределения.
Коэффициент вариации накопленной частоты по классам толщины уменьшается от значительной (100 %) в первом классе до незначительной (3 %) в девятом классе, что, очевидно, связано с пониженной экологической устойчивостью деревьев, находящихся в нижней части полога.
Библиографическая ссылка
Хлюстов В.К., Елекешева М.М. МНОГООБРАЗИЕ МАСШТАБА И ФОРМЫ СТРОЕНИЯ ДРЕВОСТОЕВ ТОПОЛЯ ЧЁРНОГО В ОСОКОРНИКАХ ПОЙМЫ РЕКИ УРАЛ // Успехи современного естествознания. 2019. № 7. С. 33-38;URL: https://natural-sciences.ru/ru/article/view?id=37156 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/use.37156



