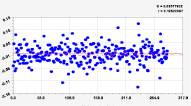
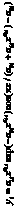Изображения, передаваемые спутниками дистанционного зондирования Земли (ДЗЗ) находят применение во многих отраслях – сельском хозяйстве, геологических и гидрологических исследованиях, лесоводстве, охране окружающей среды, планировке территорий, образовательных, разведывательных и других целях. Космические системы ДЗЗ позволяют за короткое время получить необходимые данные с больших площадей (в том числе труднодоступных и опасных участков). Одним из возможных путей анализа ДДЗ является использование подходов математической морфологии ландшафтов – направления ландшафтоведения, изучающего закономерности построения мозаик, которые образованы на земной поверхности, и разрабатывающего методы математического анализа этих мозаик [1].
До настоящего времени не существует единого обоснованного выбора вида функции. При эволюции склона должны меняться скорость смыва и осаждения материала в разных точках профиля. Это обусловливает саморазвитие склоновых систем за счет обратной связи, когда зависящий от уклона коэффициент диффузии ответственен за саму форму профиля [2].
По инструкции [3] при клике на карту открывается информационное окно, показывающее координаты, включая широту, указанной характерной точки русла реки. Нами предлагается выбирать характерные точки от истока до устья по резким изменениям кривизны в горизонтальной плоскости и после проведения измерений составить таблицу исходных данных для последующего моделирования методом идентификации устойчивых закономерностей [4].
Цель – подробный анализ асимметричных вейвлетов изменения одной координаты – приведенной к р. Ировка широты от истока до устья. При этом количество вейвлетов показывает уровень естественности рельефа территории: чем больше выявляемых волн, тем меньше происходило антропогенное влияние на изменение ландшафта малой реки.
Материалы и методы исследования
Малая река Ировка характеризуется сопряженным чередованием озеровидных расширений в семи местах от истока до устья и соединяющих их узких проток. Этот весьма распространенный тип относится к четковидным извилистым руслам, анализ строения которых и моделирования структурных параметров может внести некоторую ясность в развитие представлений о механизмах формирования русла [5].
Для междуречий р. Большой, Малой Кокшаги и Илети на территории Республики Марий Эл характерно умеренное овражное расчленение (0,02–0,05). На территории средняя лесистость составляет 34 %, распаханность – 51 %, крутизна склонов равна около 2,5 °, глубина местных базисов эрозии – 103 м. Отсутствие оврагов наблюдается в более четверти всех бассейнов рек залесенных и расположенных в подзоне южной тайги в Марийском Полесье [6].
В табл. 1 даны результаты измерений по выпискам из всплывающего окна при нажатии курсором на выбранную точку. По течению реки от истока до устья устанавливается ось абсцисс, начиная от нуля в точке истока. В этом случае местная широта образуется в направлении Север – Юг с началом в истоке реки Ировка, которая находится в прямоугольнике 23.89 минут длиной и 18.89 минут шириной.
Таблица 1
Ранговые распределения характерных точек и изменения местной широты продольного профиля русла малой реки Ировка
|
Ранг Rα |
Северная широта |
Север – Юг α, минута |
Расчетные значения |
||
|
α, минута |
ε25, минута |
∆, % |
|||
|
0 |
N56 °44.75' |
0 |
0.000 |
0 |
∞ |
|
1 |
N56 °44.73' |
0.02 |
–0.029 |
–0.0493628 |
–246.81 |
|
2 |
N56 °44.56' |
0.19 |
0.231 |
0.0407685 |
21.46 |
|
3 |
N56 °44.55' |
0.20 |
0.167 |
–0.0326814 |
–16.34 |
|
4 |
N56 °44.48' |
0.27 |
0.200 |
–0.0698822 |
–25.88 |
|
… |
… |
… |
… |
… |
… |
|
285 |
N56 °20.96' |
23.79 |
23.779 |
–0.0107833 |
–0.05 |
|
286 |
N56 °20.92' |
23.83 |
23.809 |
–0.021413 |
–0.09 |
|
287 |
N56 °20.91' |
23.84 |
23.823 |
–0.017154 |
–0.07 |
|
288 |
N56 °20.88' |
23.87 |
23.865 |
–0.0053683 |
–0.02 |
|
289 |
N56 °20.86' |
23.89 |
23.897 |
0.00741297 |
0.03 |
Колебания (вейвлет-сигналы) записываются волновой формулой [7] вида
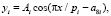
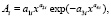
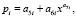 (*)
(*)
где y – показатель (зависимый фактор), i – номер составляющей (*), m – количество членов в (*), x – объясняющая переменная (влияющий фактор), a1...a8 – параметры (*), принимающие числовые значения в ходе структурно-параметрической идентификации в среде CurveExpert-1.40, Ai – амплитуда (половина) вейвлета (ось y), pi – полупериод колебания (ось x).
Результаты исследования и их обсуждение
Характерные точки выбирали визуально относительно быстро. Повышается наглядность под углом 900 космического снимка [3]. На снимке хорошо видна растительность и другие объекты, например строения и огороды вдоль русла реки.
На спутниковых снимках измерения отличаются оперативностью и возможностью быстрого измерения координат любой принятой точки, при этом измерения происходят с очень малой трудоемкостью. Из-за трудностей векторизации в сравнении с спутниковыми снимками [3] ГИС Панорама 11 имеет высокую трудоемкость.
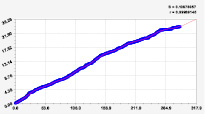
После идентификации формулы (1) было получено 25 вейвлетов (табл. 2, рис. 1–4).
Таблица 2
Параметры моделей рангового распределения местной широты реки Ировка
|
Номер i |
Вейвлет |
Коэф. кор. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
0.063641 |
1.13065 |
0.0016008 |
1 |
0 |
0 |
0 |
0 |
0.9999 |
|
2 |
0.00040393 |
3.51567 |
0.57696 |
0.58745 |
110.82755 |
–0.0022800 |
1.80206 |
0.15740 |
|
|
3 |
–0.0036181 |
0.79204 |
0 |
0 |
15.03608 |
0.023405 |
1 |
3.84747 |
|
|
4 |
1.12528e-14 |
14.62515 |
0.617963 |
1.01535 |
8.84480 |
0.247021 |
0 |
0 |
0.3931 |
|
5 |
0.00028646 |
1.02192 |
0 |
0 |
7.24585 |
0.0014330 |
1.1280 |
4.91773 |
0.3885 |
|
6 |
6.60099e-28 |
18.34451 |
0.131461 |
1.15452 |
1.25931 |
0.0308397 |
1.09014 |
19.7736 |
0.2359 |
|
7 |
5.75800e-82 |
38.2302 |
0.00700051 |
1.49880 |
15.61082 |
0 |
0 |
7.53893 |
0.5908 |
|
8 |
2.44508e-7 |
13.87948 |
2.10384 |
0.904660 |
5.95729 |
0.872172 |
1.13212 |
0.13929 |
0.1509 |
|
9 |
9.55798e-43 |
21.51899 |
0.00423083 |
1.60704 |
2.76779 |
0.0212579 |
1.00668 |
8.56668 |
0.4394 |
|
10 |
6.90749e-15 |
7.33887 |
0.0547866 |
0.999169 |
11.73840 |
0.0638034 |
0.999864 |
3.56826 |
0.1155 |
|
11 |
4.93135e-7 |
2.66385 |
0.0119845 |
1.0067 |
6.61980 |
0.00112116 |
0.963002 |
0.36049 |
0.4689 |
|
12 |
0.00040243 |
1.06255 |
0.0132666 |
0.976249 |
0.939751 |
0 |
0 |
4.50696 |
0.1544 |
|
13 |
0.00256065 |
0.742944 |
0.0117076 |
0.999885 |
2.93349 |
6.91697e-5 |
0.905847 |
0.94684 |
0.2387 |
|
14 |
2.14587e-8 |
6.29076 |
0.228905 |
0.999573 |
1.38802 |
0.00169327 |
1.00323 |
2.35141 |
0.1599 |
|
15 |
8.25269e-17 |
9.78903 |
0.353983 |
0.758466 |
2.13155 |
1.69978 |
0 |
0 |
0.2122 |
|
16 |
2.99522e-8 |
6.69529 |
0.528126 |
0.805273 |
4.39546 |
0.0011770 |
1.37960 |
2.34904 |
0.2666 |
|
17 |
1.00663e-7 |
3.18087 |
0.00075787 |
1.67431 |
5.61483 |
0 |
0 |
1.74651 |
0.3304 |
|
18 |
6.76571e-32 |
20.03587 |
0.238810 |
0.999523 |
3.11307 |
0.0306280 |
1.00022 |
1.80334 |
0.2530 |
|
19 |
1.91948e-12 |
4.19546 |
0 |
0 |
27.68004 |
0.0405511 |
1.00147 |
1.69522 |
0.2020 |
|
20 |
8.76625e-6 |
2.21622 |
0.122793 |
0.644558 |
4.76183 |
0 |
0 |
2.98586 |
0.3489 |
|
21 |
1.07760e-5 |
1.39302 |
0 |
0 |
3.99424 |
1.32155 |
0 |
0 |
0.2527 |
|
22 |
1.51462e-17 |
7.83412 |
0.0282323 |
1.02879 |
3.67720 |
0.288642 |
0 |
0 |
0.2730 |
|
23 |
1.49746e-27 |
13.20323 |
0.0599409 |
1.00062 |
5.53966 |
0.00166063 |
1.00596 |
3.56522 |
0.2418 |
|
24 |
7.48490e-8 |
3.46675 |
0.0349280 |
0.997189 |
4.57673 |
0.00043153 |
1.06958 |
0.84619 |
0.2217 |
|
25 |
1.83106e-12 |
5.41165 |
0.0312327 |
1.00042 |
6.87889 |
0.00224893 |
1.00474 |
1.86238 |
0.1262 |
|
|
|
|
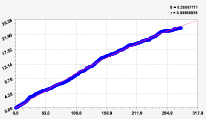
Одночленный тренд |
Первое колебание |
|
|
|
|
Второе колебание |
Тренд и два колебания |
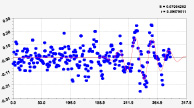
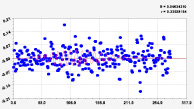
Рис. 1. Графики первых трех моделей рангового распределения широты реки Ировка
|
|
|
|
Четвертая составляющая |
Пятая составляющая |
|
|
|
|
Шестая составляющая |
Седьмая составляющая |
|
|
|
|
Восьмая составляющая |
Девятая составляющая |
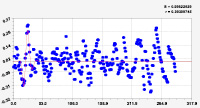
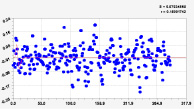
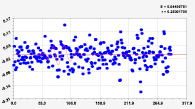
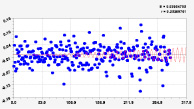
Рис. 2. Графики моделей рангового распределения широты реки Ировка (4 … 9 составляющие)
|
|
|
|
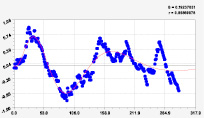
16-я составляющая |
17-я составляющая |
|
|
|
|
18-я составляющая |
19-я составляющая |
|
|
|
|
20-я составляющая |
21-я составляющая |
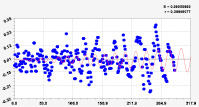
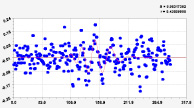
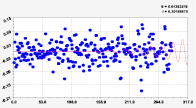
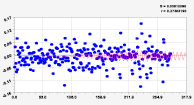
Рис. 3. Графики моделей рангового распределения широты реки Ировка (16 … 21 составляющие)
|
|
|
|
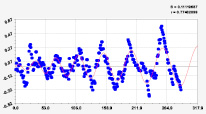
22-я составляющая |
23-я составляющая |
|
|
|
|
24-я составляющая |
25-я составляющая |
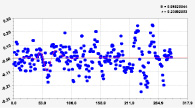
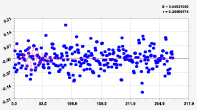
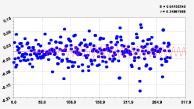
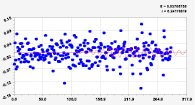
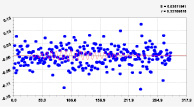
Рис. 4. Графики последних моделей рангового распределения широты р. Ировка (22 … 25 составляющие)
Остатки от 25-го колебания дали высокую погрешность моделирования в истоке реки (из-за начала координаты широты) и при первом ранге характерной точки (табл. 1). Почти до четвертого ранга летом происходит пересыхание русла малой реки Ировка. По интервалам погрешности распределились следующим образом: 0–0,1 % всего 95 шт. (32,76 %); 0–1,0 % всего 262 шт. (90,34 %); от 0 до 5 % всего 283 характерные точки русла малой реки Ировка, что составляет 97,59 % от общего количества 290 характерных точек. Норму погрешности измерений и моделирования примем до 5 %, тогда оставшиеся 290 – 283 = 7 характерных точек русла требуют отдельного рассмотрения.
Первые три вейвлета дали по возможностям программной среды CurveExpert-1.40 коэффициент корреляции 0.9099, а последующие члены получены по отдельности. Первый член является биотехническим законом [6], и он показывает часть большей волны с периодом колебания, намного большим длины малой реки Ировка. Первое колебание показывает снижение, а второе – повышение амплитуды. Остальные вейвлеты имеют свой характер.
Таким образом, географическая широта вдоль малой реки изменяется волнообразно, на что, конечно же, влияет колеблющееся расстояние между характерными точками вдоль стрежня малой реки. Причем характерные точки выбирались по резким изменениям кривизны русла. Река Ировка является простой по структуре: она имеет одно русло без островов и разветвлений. В связи с этим стрежень проходит вдоль самого русла малой реки. По-видимому, сложные структуры реки с островами и ответвлениями требуют выделения нескольких линий водотоков. Аналогичные рис. 2 графики получены для вейвлетов 10–15.
На рис. 3 заметны несколько коротких по характерным точкам вейвлетов.
При этом 16-я составляющая общей модели (*) находится почти около истока Ировки. Из-за обмеления многих малых рек, по-видимому, именно из-за этого резкого колебания географических координат (аналогично и по долготе) около истока реки появляются пересыхающие летом участки. 19-я составляющая показывает переход колебания широты после устья малой реки Ировка. Колебательная адаптация русла малой реки к рельефу местности происходит за долгое время. Для реки Ировка, судя по четковидной структуре, рельеф изменился в конце последнего оледенения примерно 12 тысяч лет назад. С тех пор колебания земной коры привели к сложной структуре изменения в рельефе местности, в частности широты характерных точек русла реки. На длине в 69 км реки Ировка имеются семь озеровидных расширений и четыре притока. Поэтому бассейн р. Ировка на площади 917 км2 получает еще большую сложность в колебательных изменениях географических координат.
На рис. 4 приведены графики колебаний широты по последним вейвлетам. Все они являются конечномерными колебаниями, находящимися внутри длины малой реки Ировка.
После 25-го члена (*) процесс квантования вейвлетов сильно затрудняется. Поэтому условно можно принять, что он становится границей квантовой определенности для широты. Для продолжения квантования нужно повысить точность измерений. Во всяком случае, пока нет уверенности в том, что рельеф получает квантовую запутанность, как это происходит при моделировании асимметричными вейвлетами динамики метеорологических параметров.
Заключение
Спутниковые снимки в программной среде по инструкции [3] позволяют оперативно изучать территорию малых рек и составлять таблицы координат, в частности по местной широте, для статистического моделирования. При этом особое значение приобретает волновое изменение местной широты от Севера на Юг (от истока до устья малой реки Ировка).
Изменение местной широты по рангам характерных точек вдоль стрежня русла малой реки Ировка позволило идентифицировать 25 членов в виде асимметричных вейвлетов. Причем все 25 вейвлетов являются конечномерными, то есть каждый из них имеет начало и конец колебательной адаптации к долговременным изменениям рельефа. При этом значительная часть колебаний происходит внутри общей длины реки Ировка длиной 69 км.
Первые три члена дали коэффициент корреляции 0.9099, уровень адекватности более 0.9 или сильнейшей связи. Остальные 22 члена повышают уровень адекватности почти до 1. Местная широта малой реки Ировка по измерениям на космических снимках 2015 г. дает высокую определенность процесса квантования. Поэтому метод [7] идентификации изменения координат точек русла рекомендуется для изучения структуры и других малых рек.
Библиографическая ссылка
Мазуркин П.М., Георгиева Я.О. ВЕЙВЛЕТ-АНАЛИЗ РАСПРЕДЕЛЕНИЯ ШИРОТЫ В ХАРАКТЕРНЫХ ТОЧКАХ ПРОДОЛЬНОГО ПРОФИЛЯ РУСЛА МАЛОЙ РЕКИ ИРОВКА // Успехи современного естествознания. 2019. № 12-1. С. 89-95;URL: https://natural-sciences.ru/ru/article/view?id=37274 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/use.37274