Из определения прибрежных дюн – форм рельефа, сформировавшихся посредством переноса и переотложения песков у песчаных пляжей, состояние пляжей для устойчивости дюн играет важнейшую роль [1]. Развитие дюны происходит у пляжей при синхронизации транспортирующего потенциала (силы и направления ветра) с наносами, доступными на пляже или поступающими при воздействии гидродинамических процессов. Доступность наносов для эолового перемещения связано с понятием полосы насыщения ветропесчаного потока [2]. В формировании полосы насыщения – ширина незатопленной части пляжа является важнейшим параметром, наряду со скоростью и направлением ветра [3; 4]. Ширина затопления пляжа зависит от прибрежных гидродинамических условий (высоты и длины волнения) и высоты нагона моря, соответственно может сокращать доступность наносов для эолового перемещения либо быть фактором абразии прибрежных дюн.
В районах, где не ведется регулярных наблюдений за прибрежным волнением, к которому относится и исследуемый в настоящей работе район (морской аккумулятивный берег Куршской косы), возможно выполнить математическое моделирование для получения параметров ветрового волнения в акватории с целью определения ширины затопления пляжа. Для целей работы было выполнено численное моделирование ветрового волнения с использованием волновой спектральной модели третьего поколения SWAN версии 41.20A [5]. Модель создана для расчета параметров ветрового волнения в прибрежной зоне исходя из рельефа дна и скорости ветра. Модель SWAN для расчета параметров ветрового волнения в прибрежной зоне моря широко используется в мире и доказала свою эффективность [6–8]. С использованием данной модели в юго-восточной части Балтийского моря ранее производились расчеты различных параметров ветрового волнения [9–11]. Модель была верифицирована для использования в Балтийском море [11–13], в том числе в прибрежной зоне.
Для использования в условиях мелководья в модели SWAN реализованы трехкомпонентные схемы взаимодействия волн и две схемы, отвечающие за трение о дно и обрушение волн или диссипацию. При расчете учитываются следующие процессы: распространение волн в пространстве, рефракция (дно и течения), дифракция и др. Среди процессов диссипации и генерации: ветровая генерация, нелинейное взаимодействие (триады), диссипации из-за: обрушения, обрушения, связанного с изменением глубин, диссипация из-за трения о дно.
Цель исследования состояла в применении модельного подхода для определения ширины затопления пляжа на морском аккумулятивном берегу в задачах научно обоснованного управления прибрежной зоной и дюнным валом Куршской косы.
Материалы и методы исследования
Исходные гидрометеорологические данные
Поскольку пространственные размеры исследуемого района находятся в пределах 16х27 км, а в непосредственной близости в отрытом море находится действующая метеостанция, в качестве входных данных модели используются сила и направление ветра, полученные с МЛСП Д-6. Результаты реанализа метеополей (например, NCEP/CFSR), как это используется в ряде работ [11–15], покрывают исследуемый район лишь двумя ячейками, а СКО (среднеквадратическая ошибка), в сравнении с метеопостами, составляет 3,43–1,33 м/с [16]. Дискретность данных по силе и направлению ветра составляла 3 часа. От пунктов наблюдения за шириной затопления пляжа (14 и 42 км Куршской косы) станция удалена на 26.6 и 15.8 км соответственно. Данные по уровню Балтийского моря получены с поста 86179 Пионерский (Калининградский ЦГМС). Дискретность данных уровня моря составляет 6 часов, а «0» поста установлен на отметке 500 см.
Исходная батиметрическая основа и расчетная сетка модели SWAN
Цифровая модель рельефа дна была построена с использованием ESRI ArcGIS 10.0 по объединенным батиметрическим данным из различных источников: сечением 5 м для глубин более 50 м [17], сечением 1 м, построенным по морским планам ГУНиО, сечением 0,1–0,2 м до глубин 2 м (на основе собственных измерений). Батиметрические данные были объединены (рис. 1, а) с использованием инструмента Merge, на основе чего была построена цифровая модель дна на регулярной сетке (размер ячейки 5 м).
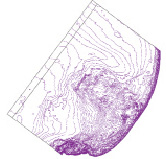
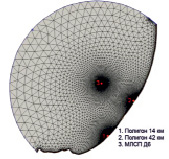
а) б)
Рис. 1. Цифровая модель рельефа дна: а) исходные батиметрические данные для построения модели дна; б) нерегулярная расчетная сетка ADCIRC
Для исследуемой области была построена нерегулярная расчетная сетка ADCIRC, с. Конечно элементная сетка выполнена триангуляцией, которая хорошо аппроксимирует кривую береговой линии, поскольку количество узлов рассчитывается исходя из количества точек на береговой линии. В областях интереса (полигоны наблюдения за шириной затопления пляжа, платформа Д6) расчетная сетка сгущена для лучшего отображения рельефа дна, в особенности вблизи береговой линии. Вблизи полигонов, а также у платформы Д6 шаг сетки составляет 20–100 м, в глубоководной части сетка разряжена до шага 5 км. Радиус окружности расчетной сетки выбран таким образом, чтобы длина разгона ветровых волн могла составлять не менее 150 км. Всего расчетная сетка состоит из 73 200 расчетных узлов.
Параметры моделирования: координаты прямоугольные, зональные WGS84 UTM34N, режим GEN3, со следующими параметрами: экспоненциальная схема роста Komen [18] с включенным правилом Agrow. Донное трение принято Friction Jonswap Constant cf 0.071. Включены процессы: забурунивание; трехкомпонентное волновое взаимодействие, разрушение волн. Выходные данные в модели общего расчета формируются в виде файла граничных условий и волнового спектра, а также таблицы с основным и дополнительными параметрами волнения: время (T); высота значительных волн (Hs), м; длина волны (Wlen), среднее направление волны (WDir), гр., и др. Моделирование c использованием волновой модели SWAN выполнялось для пятилетнего периода 2014–2019 гг., с шагом 3 часа.
Моделирование высоты волнового наката и ширины затопления пляжа
Расчет высоты волнового наката был выполнен согласно приложению Д, СП 38.13330.2018 [19], применяемого в проектировании берегозащитных сооружений в России, а также по адаптированной для юго-восточной Балтики модели волнового наката [20] (уравнение 1):
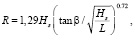 (1)
(1)
где Hs – высота значительных волн, м; L – длина волны, м; β – уклон пляжа.
По результатам полученной высоты волнового наката был выполнен расчет ширины затопления пляжа (BI) (уравнение 2):
BI = (R + S)*ctg (β), (2)
где R – высота волнового наката, полученная посредством расчетов по СП 38.13330.2018 или адаптированной модели; S – высота уровня моря, м; β – уклон пляжа.
Уклон пляжа определялся по данным мониторинга за состоянием дюнного вала Куршской косы, выполнявшегося с 2014 г., в рамках которого выполнялись наблюдения за шириной затопления пляжа in situ [4; 21].
Результаты исследования и их обсуждение
Моделирование ветрового волнения
Первым этапом выполняемого исследования являлось сравнение результатов выполненного моделирования ветрового волнения c использованием волновой модели SWAN (далее – SWAN) с данными по ветровому волнению из общедоступных источников (E.U. Copernicus Marine Service (далее – Copernicus) – использующих волновую модель WAM 4.6), а также измерений с использованием уровнемера-волнографа, установленного на морской платформе Д6 (рис. 1). Сравнение и сопоставление результатов проводилось для результатов 2019 г., с шагом 3 часа. Всего использовалось 2375 пар сравнения наблюдений и модельных значений (рис. 2).
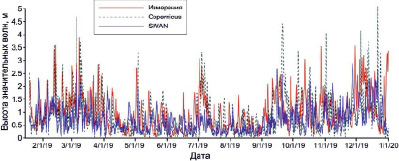
Рис. 2. Значительная высота волн у платформы Д6 в 2019 г. по данным измерений, материалам Copernicus и выполненного моделирования SWAN
По графику годового хода значительной высоты волн наблюдаемая разница между полученными с использованием SWAN высотами значительных волн и полученная по результатам прямых измерений, вероятно, связана с дискретностью используемых метеорологических данных. Моделированные значения имеют более плавный ход, в отличие от наблюдаемых, что свидетельствует о том, что локальные флуктуации волнения не передаются в полном объеме [11]. Существенно выбиваются пики максимальных значений по данным Copernicus, что может быть связано с существенно более грубой используемой сеткой моделирования (2х2 км у Copernicus, 0,02х0,02 км у SWAN). Скаттер диаграммы измеренных и моделированных значений приведен на рис. 3.
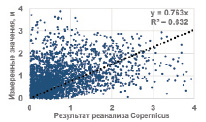
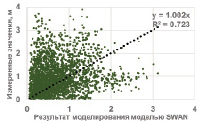
а) б)
Рис. 3. Скаттер диаграммы измеренных и моделированных значений: а) Copernicus и измеренные значения; б) SWAN и измеренные значения
Величины коэффициентов корреляции между измеренными значениями и данными моделирования SWAN и Copernicus составили 0,81 и 0,69 соответственно, что весьма удовлетворительно, с учетом использования данных одной метеорологической станции в качестве входных данных. Наклоны линейных трендов между измеренными и моделированными значениями находились в пределах 1–0,7, с достоверностью аппроксимации R2 0,723 и 0,632, что демонстрирует более высокое качество работы используемой модели SWAN для моделирования ветрового волнения в сравнении с данными Сopernicus. Для статистической оценки качества моделирования был рассчитан ряд статистических параметров – среднеквадратическая ошибка (СКО), средняя ошибка и средняя абсолютная ошибка (табл. 1).
Таблица 1
Статистические характеристики сравнения измеренных данных с моделированными
|
Статистический показатель |
Значение |
|
СКО (Измерения/Copernicus) |
0,54 |
|
СКО (Измерения/SWAN) |
0,38 |
|
Средняя ошибка (Измерения/Copernicus) |
0,35 |
|
Средняя ошибка (Измерения/SWAN) |
0,31 |
|
Средняя абсолютная ошибка (Измерения/Copernicus) |
0,45 |
|
Средняя абсолютная ошибка (Измерения/SWAN) |
0,29 |
По результатам проведенных статистических тестов данные по глобальному анализу для рассматриваемой части акватории Балтийского моря имеют большее отклонение от измеренных значений (СКО = 0,54); для анализа, основанного на WAM, это является приемлемым показателем [22; 23]. При этом полученные посредством SWAN результаты (СКО = 0,38) сопоставимы, а также несколько выше, чем в ранее приводимых исследованиях [11; 24], что связано с использованием густой расчетной сетки и относительно локализованного, прибрежного участка моделирования. Эти факты обоснованно позволили принять результаты моделирования ветрового волнения с использованием модели SWAN в качестве гидродинамических условий для моделирования ширины затопления пляжа.
Моделирование ширины затопления пляжа и сравнение полученных результатов
На втором этапе был выполнен расчет ширины затопления пляжа на основе стандарта СП 38.13330.2018, а также по адаптированной для юго-восточной Балтики модели. Результаты моделирования были сопоставлены с данными натурных наблюдений на берегу Куршской косы (рис. 4).
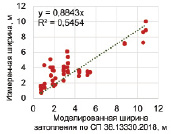
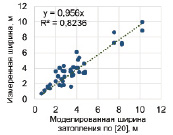
а) б)
Рис. 4. Скаттер диаграммы измеренных и моделированных значений: а) СП 38.13330.2018 и измеренные значения; б) [20] и измеренные значения
По результатам сравнения ширины затопления пляжа по адаптированной модели и СП 38.13330.2018 первая показала существенное преимущество в точности определения ширины затопления пляжа. СКО составила по результатам сравнения 0,73, при средней абсолютной ошибке определения ширины в 0,52 м. Статистические характеристики приведены в табл. 2.
Таблица 2
Статистические характеристики сравнения измеренных данных с моделированными
|
Статистический показатель |
Значение |
|
СКО (Измерения/СП 38.13330.2018) |
1,82 |
|
СКО (Измерения/[20]) |
0,73 |
|
Средняя ошибка (Измерения/СП 38.13330.2018) |
0,16 |
|
Средняя ошибка (Измерения/[20]) |
0,02 |
|
Средняя абсолютная ошибка (Измерения/СП 38.13330.2018) |
1,61 |
|
Средняя абсолютная ошибка (Измерения/[20]) |
0,52 |
Несмотря на рекомендацию по использованию при расчете высоты наката волн использовать натурные наблюдения, которые чаще всего отсутствуют, СП 38.13330.2018 предлагает расчетную методику, которая может быть обобщена на побережье морей России. По проведенному сравнению с натурными данными локальные адаптации расчета существенно превосходят полученные при руководстве нормой результаты (СКО для СП 38.13330.2018 составила 1,82). Таким образом, при проведении научных исследований следует подбирать локальные адаптации моделей волнового наката, точнее характеризующие гидродинамический процесс [20; 25].
Заключение
Проведенное исследование показало возможность и непосредственное сочетание моделирования ветрового волнения с использованием спектральной волновой модели с моделированием ширины затопления пляжа. По результатам сравнения с натурными данными уровнемера-волнографа на платформе Д6, данными E.U. Copernicus Marine Service результаты моделирования SWAN существенно выше, чем в глобальной модели, несмотря на использование данных одного метеопоста, установленного в открытом море. Выполненное моделирование ширины затопления пляжа с использованием национальных методик и регионально адаптированной модели волнового наката показало значительное улучшение качества определения ширины с использованием локальных моделей. При проведении исследования ширины затопления пляжа как лимитирующего фактора развития прибрежных дюн большую репрезентативность результатов можно получить при использовании региональной адаптации. Однако для большей достоверности расчетов следует производить регулярные наблюдения за состоянием пляжей, что позволит существенно улучшить качество производимых оценок. Научно обоснованные и точные оценки могут позволить принять рациональное решение по защите и восстановлению прибрежных дюн Национального парка «Куршская коса», имеющих важное экологическое и культурное значение.
Исследование выполнено при финансовой поддержке РФФИ и Калининградской области в рамках проекта № 19-45-393001. Сбор данных волнографа был выполнен при поддержке госзадания ИО РАН (тема № 0149-2019-0013).
Библиографическая ссылка
Данченков А.Р. МОДЕЛИРОВАНИЕ ВЕТРОВОГО ВОЛНЕНИЯ И ШИРИНЫ ЗАТОПЛЕНИЯ ПЛЯЖА ДЛЯ ИССЛЕДОВАНИЙ ПРИБРЕЖНЫХ ДЮН НАЦИОНАЛЬНОГО ПАРКА «КУРШСКАЯ КОСА» // Успехи современного естествознания. 2020. № 3. С. 65-71;URL: https://natural-sciences.ru/ru/article/view?id=37347 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/use.37347



